苏科版初中数学七年级上册第六单元《平面图形的认识（一）》单元测试卷（较易）（含答案解析）

苏科版初中数学七年级上册第六单元《平面图形的认识（一）》单元测试卷

考试范围：第六章  考试时间 ：120分钟  总分 ：120分

第I卷（选择题）

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分如图，发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是(    )

A. 两点之间线段最短
B. 两点确定一条直线
C. 垂线段最短
D. 经过直线外一点，有且只有一条直线与这条直线平行
 

2.下列说法不正确的是(    )
 

A. 直线与直线是同一条直线 B. 射线与射线是同一条射线
C. 射线与射线是同一条射线 D. 线段与线段是同一条线段

3.如图，用圆规比较两条线段和的长短，其中正确的是(    )

 

A.  B.
C.  D. 没有刻度尺，无法确定

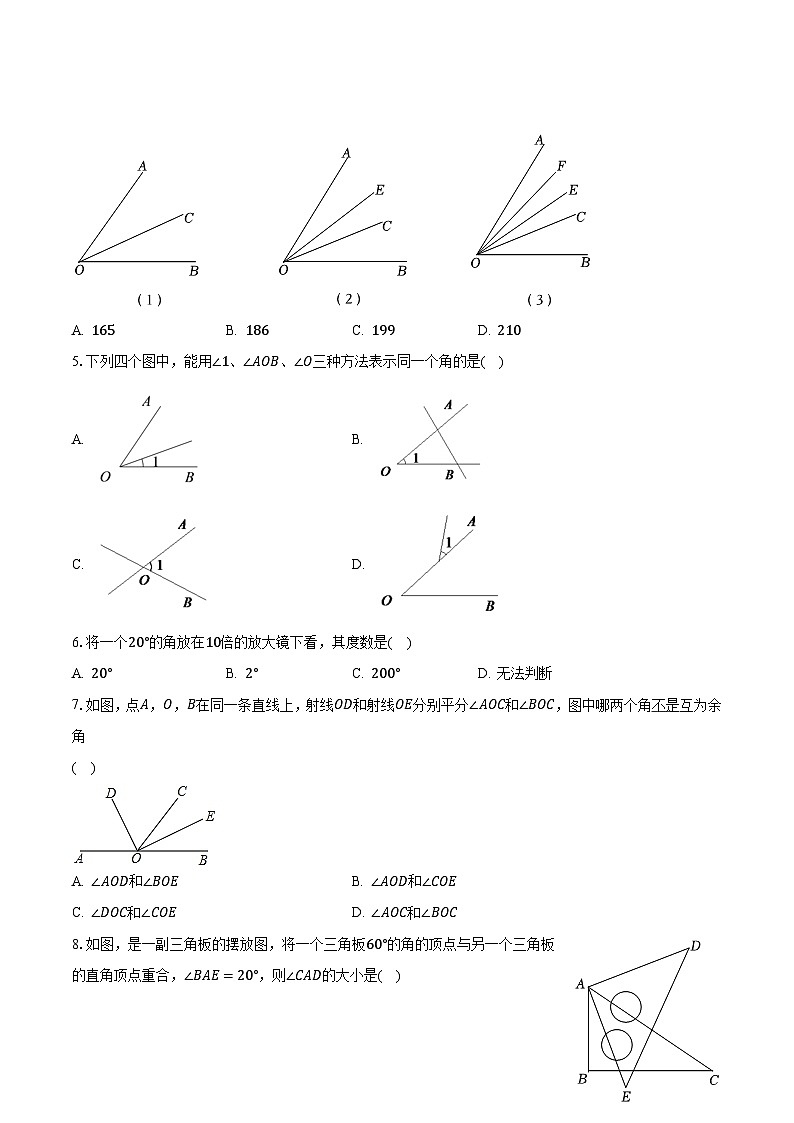
4.在锐角内部，画出条射线，可以画出个锐角；画出条不同的射线，可以画出个锐角；画出条不同的射线，可以画出个锐角．照此规律，画条不同的射线，可以画出锐角的个数为(    )

 

A.  B.  C.  D.

5.下列四个图中，能用、、三种方法表示同一个角的是(    )

A.  B.
C.  D.

6.将一个的角放在倍的放大镜下看，其度数是(    )

A.  B.  C.  D. 无法判断

7.如图，点，，在同一条直线上，射线和射线分别平分和，图中哪两个角不是互为余角
(    )
 

A. 和 B. 和
C. 和 D. 和

8.如图，是一副三角板的摆放图，将一个三角板的角的顶点与另一个三角板的直角顶点重合，，则的大小是(    )

A.
B.
C.
D.

9.曲桥是我国古代经典建筑之一，它的修建增加了游人在桥上行走的路程，有利于游人更好地观赏风光．如图，、两地间修建曲桥与修建直的桥相比，增加了桥的长度，其中蕴含的数学道理是(    )

A. 两点之间，线段最短
B. 平行于同一条直线的两条直线平行
C. 垂线段最短
D. 两点确定一条直线

10.在同一平面内，不重合的两条直线的位置关系是
(    )

A. 平行 B. 相交 C. 平行或相交 D. 平行、相交或垂直

11.春节过后，某村计划挖一条水渠将不远处的河水引到农田记作点，以便对农田的小麦进行灌溉，现设计了如图所示的四条路段，，，，其中最短的一条路线是(    )

 

A.  B.  C.  D.

12.如图，直线、相交于点，过作，且平分，则的度数是(    )

A.
B.
C.
D.

第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）

13.两条线段，一条长，另一条长，将它们一端重合且放在同一条直线上，则这两条线段的中点之间的距离是______ ．

14.已知，在的外部作射线，则与的关系可能是__________．

；；

．

15.如果一个角的余角度数为，那么这个角的补角度数为______ ．

16.如图，想在河两岸搭建一座桥，图中搭建方式中，最短的是______．

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17.本小题分

在平面内有三点，，，
当，，三点不共线时，如图，画直线，线段，射线，在线段上任取一点不同于点，，连接，并数一数，此时图中共有多少条线段．
当，，三点共线时，若，，点，分别是线段，的中点，求线段的长画出图形并写出计算过程

18.本小题分

如图，已知，点为的中点，为上一点，点为的中点，且，求的长．

19.本小题分
如图，，若，则 ______ ；若，则 ______ ；
如图，，则与又有怎样的数量关系，请说明理由；
如图，已知，都是锐角，若把它们的顶点重合一起，请直接写出与的数量关系，不必说明理由．

 

20.本小题分

如图，，，三点共线，，求的度数．

21.本小题分

已知点是直线上的点，．
图中与互补的角有______ ，______ ；
如果射线、分别表示从点出发的东、西两个方向，那么射线表示______ 请填方位角；
画不要求写画法

22.本小题分

如图所示，取一张长方形的硬纸板，将硬纸板对折使与重合，为折痕．把长方形平放在桌面上，另一个面无论怎么改变位置总有存在，你知道为什么吗？

23.本小题分

如图，为直线外一点，以为端点引两条射线，，使，，、、三点在同一条直线上吗为什么

24.本小题分

如图，和交于点，平分，于点，求的度数．

25.本小题分
已知、相交于点，于，平分，且，求的度数．

答案和解析

1.【答案】 

【解析】解：某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分如图，发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是两点之间线段最短．
故选：．
根据两点之间，线段最短进行解答．
此题主要考查了线段的性质，关键是掌握两点之间，线段最短．

2.【答案】 

【解析】略

3.【答案】 

【解析】由题图可知，，故选C．

4.【答案】 

【解析】解：在锐角内部，画条射线，可得个锐角；
在锐角内部，画条射线，可得个锐角；
在锐角内部，画条射线，可得个锐角；
从一个角的内部引出条射线所得到的锐角的个数是
，
画条不同射线，可得锐角．
故选：．
分别找出各图形中锐角的个数，找出规律解题．
此题考查了角的概念，解决改题的关键是找到规律，从一个角的内部引出条射线所得到的锐角的个数是．

5.【答案】 

【解析】【分析】
本题考查的是角的概念有关知识熟知“如果只有一个单独的角，可以用它的顶点字母表示；可以用三个大英文字母表示，而且表示顶点的字母必须放在中间；当一个角的内部不再包含其他角时，可以在角的内部靠近顶点处加上弧线，注上数字或小写希腊字母表示一个角”等，这三点是解题的关键利用角的概念对选项逐一判断即可解答．
【解答】
解：不能用表示其中的一个角，表示的角和不是一个角；
B.符合角的表示概念知识，可以表示同一个角；
C.两线交叉有四个角，不能用表示其中的一个角；
D.表示的与、不是一个角．
故选B．

6.【答案】 

【解析】解：由分析可知：一个角度数为度，在倍的放大镜下观察，这个角的度数为度，
故选：．
因为角是从同一点引出的两条射线组成的图形，它的大小与图形的大小无关，只与两条射线形成的夹角有关系．
本题考查了角的概念，掌握从同一点引出的两条射线组成的图形叫做角是解题的关键．

7.【答案】 

【解析】【分析】
本题考查了角平分线的定义，余角的判断，属于简单题，熟悉角平分线的概念是解题关键．

根据角平分线定义找到相等的角，利用平角是，再根据两个角相加为即为互余，即可解题．

【解答】

解：射线和射线分别平分和，

，，

，

，，，

故选D．

8.【答案】 

【解析】解：由题意得：，，
，
，
，
，
故选：．
根据题意可求得，再由可求得的度数．
本题主要考查余角，解答的关键是结合图形分析清楚各角之间的关系．

9.【答案】 

【解析】解：这样做增加了游人在桥上行走的路程，其中蕴含的数学道理是：利用两点之间线段最短，可得出曲折迂回的曲桥增加了游人在桥上行走的路程．
故选：．
利用两点之间线段最短分析得出答案．
此题主要考查了两点之间线段最短，正确将实际问题转化为数学知识是解题关键．

10.【答案】 

【解析】解：在同一平面内，不重合的两条直线只有两种位置关系，平行或相交，
所以在同一平面内，不重合的两条直线的位置关系是：平行或相交．
故选：．
根据直线的位置关系解答．
本题考查了两直线的位置关系，需要特别注意，垂直是相交的特殊形式．在同一平面内，不重合的两条直线只有平行或相交两种位置关系．

11.【答案】 

【解析】【分析】
本题考查了垂线段最短的性质，根据垂线段的性质：垂线段最短，可得答案．

【解答】
解：根据图示可知，于是点到直线的距离中，最短的距离是的长度．

故选B．

12.【答案】 

【解析】解：，
，
平分，
，
．
故选：．
先根据垂直的定义得：，由角平分线的定义得，最后根据邻补角的定义可得结论．
此题主要考查了邻补角，垂直定义和角平分线的性质，关键是掌握垂直得直角，邻补角互补．

13.【答案】或 

【解析】解：设较长的线段为，较短的线段为，
分两种情况：
当两条线段在重合一端的同侧，如图：

点是的中点，点是的中点，
，，
，
当两条线段在重合一端的异侧，如图：

点是的中点，点是的中点，
，，
，
所以，两条线段的中点之间的距离是或．
故答案为：或．
分两种情况，两条线段在重合一端的同侧，两条线段在重合一端的异侧．
本题考查了两点间距离，掌握分类讨论思想，根据题目的已知条件画出图形是关键．

14.【答案】 

【解析】【分析】

略

【解答】
略

15.【答案】 

【解析】解：一个角的余角度数为 ，
这个角的度数为，
这个角的补角的度数为，
故答案为：．
根据余角与补角的定义求解即可：如果两个角的度数之和为度，那么这两个角互余；如果两个角的度数之和为度，那么这两个角互补．
本题主要考查了余角与补角的计算，熟知余角与补角的定义是解题的关键．

16.【答案】 

【解析】解：因为，垂足为，则为垂线段，根据的是垂线段最短．
故答案为：．
根据从直线外一点到这条直线上各点所连的线段中，垂线段最短，可知搭建方式最短的是，理由是垂线段最短．
本题考查了垂线的性质：从直线外一点到这条直线上各点所连的线段中，垂线段最短．比较简单．

17.【答案】解：作图如下：

此时图中共有条线段；
解：有两种情况：
当点在线段的延长线上时，如图：

因为，分别是，的中点，，，
所以，
所以；
当点在线段上时，如图：

根据题意，如图，，，
所以，
综上可知，线段的长度为或． 

【解析】根据直线，射线，线段的概念，利用直尺即可作出图形；
根据线段的定义即可求解．
本题考查了两点间的距离，线段、射线以及线段的作图，是一个基础题，在作图的过程中要注意延伸性．

18.【答案】解：，是的中点，
，
又为的中点，，
，
． 

【解析】本题主要考查了两点间的距离，线段的和差及线段中点的定义，根据线段中点的定义求出，，再由，可得出答案．

19.【答案】   

【解析】解：，，
，
，
，
，，
，
，
，
故答案为：，；
；
理由：，
，
，
，
；
；
理由：，
，
，
，
．
根据，求出的度数，继而根据即可求出的度数；根据，，即可求出的度数，再根据即可求出的度数；
根据得出，再根据，得出，从而得到；
根据得出，再根据得出，从而得出．
本题考查了角的计算，熟练掌握角的和差计算是解题的关键．

20.【答案】 

【解析】略

21.【答案】    北偏西 

【解析】解：，
，
图中与互补的角有和，
故答案为：，；
过点作，
，
，
射线表示北偏西；
故答案为：北偏西；
如图所示，
根据补角的定义即可得到结论；
过点作，根据余角的性质即可得到结论；
根据题意作出图形即可．
本题考查了补角的定义，方向角，角平分线的定义，熟练掌握角平分线的定义是解题的关键．

22.【答案】解：； 
理由： 
，， 
． 

【解析】根据平行公理的推论得出答案即可． 
此题主要考查了平行公理的推论，熟练掌握相关的定理是解题关键．

23.【答案】解：、、三点在同一条直线上．
理由如下：
因为，，且，都经过点，
又为直线外一点，根据“经过直线外一点，有且只有一条直线与这条直线平行”知，，在同一条直线上，
所以、、三点在同一条直线上． 

【解析】本题主要考查两点确定一条直线相关知识解决本题的关键是利用“经过直线外一点，有且只有一条直线与这条直线平行”这个性质用这个性质时一定要注意点必须在直线外，另外“有且只有”强调了直线的存在性和唯一性．

24.【答案】解：、相交于点，
．
平分，
，
，
，
． 

【解析】对顶角由角平分线的定义推知；然后结合垂直的定义易求的度数．
本题考查了对顶角、邻补角，角平分线的定义等知识点．要注意领会由垂直得直角这一要点．

25.【答案】解：，
，
平分，，
，
，
． 

【解析】本题考查垂直的定义、角平分线的定义、对顶角相等的性质，以及角的和差计算等知识，正确识图是解决问题的关键．
根据垂直的定义得，根据角平分线的定义得，根据角的和差关系求得的度数，再根据对顶角相等的性质求出答案．