2023年二轮复习解答题专题四：一次函数的应用图象型

这是一份2023年二轮复习解答题专题四：一次函数的应用图象型，文件包含2023年二轮复习解答题专题四一次函数的应用图象型原卷版docx、2023年二轮复习解答题专题四一次函数的应用图象型解析版docx等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。
2023年二轮复习解答题专题四：一次函数的应用图象型方法点睛图象型应用题：找到函数图象上两个点的坐标,根据待定系数法求得函数解析式；若函数图象为分段函数,注意要取同段函数图象上的两点,依此方法分别求每段函数图象的解析式,最后记得加上对应自变量的取值范围. 典例分析类型一  行程问题例1     （2022天津中考） 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．已知学生公寓、阅览室、超市依次在同一条直线上，阅览室离学生公寓，超市离学生公寓，小琪从学生公寓出发，匀速步行了到阅览室；在阅览室停留后，匀速步行了到超市；在超市停留后，匀速骑行了返回学生公寓．给出的图象反映了这个过程中小琪离学生公寓的距离与离开学生公寓的时间之间的对应关系．请根据相关信息，解答下列问题：（1）填表：离开学生公寓的时间/585087112离学生公寓的距离/0.5  1.6  （2）填空：①阅览室到超市的距离为___________；②小琪从超市返回学生公寓的速度为___________；③当小琪离学生公寓的距离为时，他离开学生公寓的时间为___________．（3）当时，请直接写出y关于x的函数解析式．类型二  其他问题例2     （2022吉林中考） 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水，甲壶比乙壶加热速度快．在一段时间内，水温（℃）与加热时间之间近似满足一次函数关系，根据记录的数据，画函数图象如下：（1）加热前水温是          ℃；（2）求乙壶中水温关于加热时间的函数解析式；（3）当甲壶中水温刚达到80℃时，乙壶中水温是          ℃．专题过关1. （2022盐城中考）小丽从甲地匀速步行去乙地，小华骑自行车从乙地匀速前往甲地，同时出发．两人离甲地的距离与出发时间之间的函数关系如图所示．
小丽步行的速度为______；
当两人相遇时，求他们到甲地的距离．
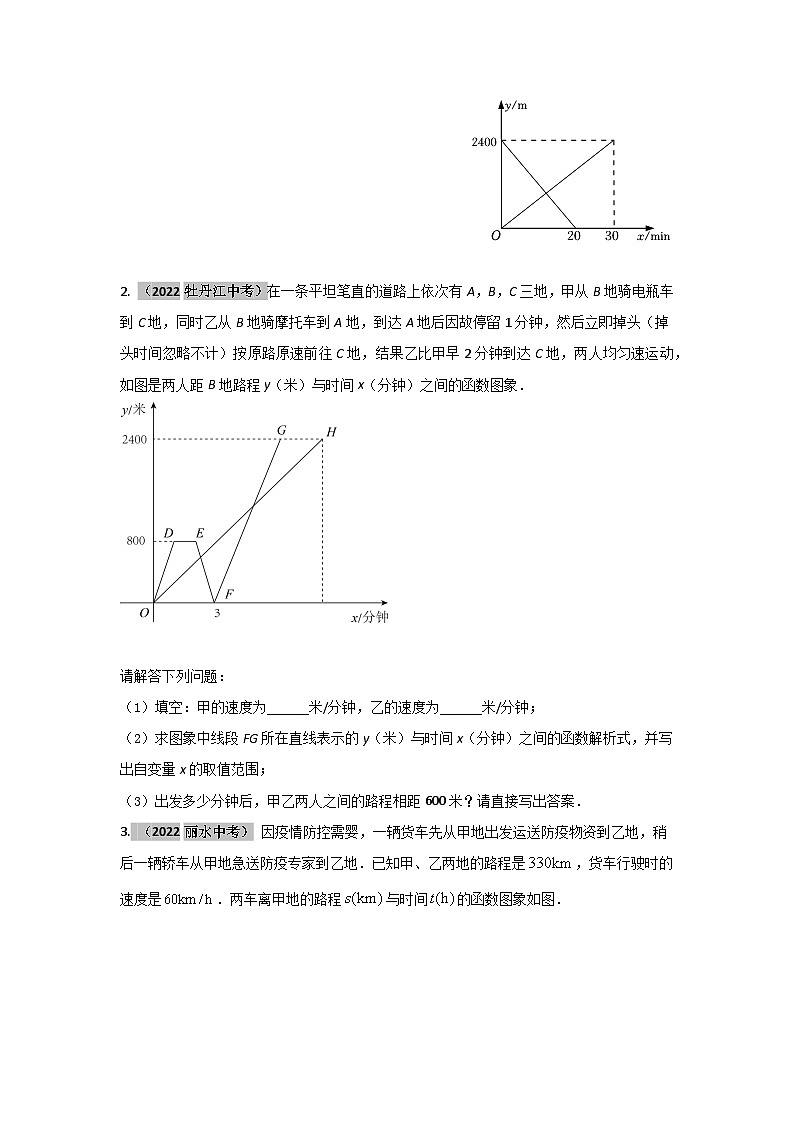
2. （2022牡丹江中考）在一条平坦笔直的道路上依次有A，B，C三地，甲从B地骑电瓶车到C地，同时乙从B地骑摩托车到A地，到达A地后因故停留1分钟，然后立即掉头（掉头时间忽略不计）按原路原速前往C地，结果乙比甲早2分钟到达C地，两人均匀速运动，如图是两人距B地路程y（米）与时间x（分钟）之间的函数图象．
 请解答下列问题：（1）填空：甲的速度为______米/分钟，乙的速度为______米/分钟；（2）求图象中线段FG所在直线表示的y（米）与时间x（分钟）之间的函数解析式，并写出自变量x的取值范围；（3）出发多少分钟后，甲乙两人之间的路程相距600米？请直接写出答案．3. （2022丽水中考） 因疫情防控需婴，一辆货车先从甲地出发运送防疫物资到乙地，稍后一辆轿车从甲地急送防疫专家到乙地．已知甲、乙两地的路程是，货车行驶时的速度是．两车离甲地的路程与时间的函数图象如图．
 （1）求出a的值；（2）求轿车离甲地的路程与时间的函数表达式；（3）问轿车比货车早多少时间到达乙地？4. （2022湖州中考） 某校组织学生从学校出发，乘坐大巴前往基地进行研学活动．大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶．已知大巴行驶的速度是40千米/小时，轿车行驶的速度是60千米/小时．（1）求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？（2）如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象．试求点B的坐标和AB所在直线的解析式；（3）假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时追上大巴，求a的值．5. （2022新疆兵团中考） A，B两地相距，甲、乙两人分别开车从A地出发前往B地，其中甲先出发，如图是甲，乙行驶路程随行驶时间变化的图象，请结合图象信息．解答下列问题：（1）填空：甲的速度为___________；（2）分别求出与x之间的函数解析式；（3）求出点C的坐标，并写点C的实际意义．6. （2022成都中考） 随着“公园城市”建设的不断推进，成都绕城绿道化身成为这座城市的一个超大型“体育场”，绿道骑行成为市民的一种低碳生活新风尚．甲、乙两人相约同时从绿道某地出发同向骑行，甲骑行的速度是，乙骑行的路程与骑行的时间之间的关系如图所示．
 （1）直接写出当和时，与之间的函数表达式；（2）何时乙骑行在甲的前面？7. （2022长春中考） 己知A、B两地之间有一条长440千米的高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车先以100千米/时的速度匀速行驶200千米后与乙车相遇，再以另一速度继续匀速行驶4小时到达B地；乙车匀速行驶至A地，两车到达各自的目的地后停止．两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数关系如图所示．（1）_______，_______；（2）求两车相遇后，甲车距A地的路程y与x之间的函数关系式；（3）当乙车到达A地时，求甲车距A地的路程．8. （2022包头中考） 由于精准扶贫的措施科学得当，贫困户小颖家今年种植的草莓喜获丰收，采摘上市16天全部销售完．小颖对销售情况进行统计后发现，在该草莓上市第x天（x取整数）时，日销售量y（单位：千克）与x之间的函数关系式为草莓价格m（单位：元/千克）与x之间的函数关系如图所示．
 （1）求第14天小颖家草莓的日销售量；（2）求当时，草莓价格m与x之间的函数关系式；（3）试比较第8天与第10天的销售金额哪天多？9. （2022鄂州中考） 在“看图说故事”话动中，某学习小组设计了一个问题情境：小明从家跑步去体育场，在那里锻炼了一阵后又走到文具店买圆规，然后散步走回家．小明离家的距离y（km）与他所用的时间x（min）的关系如图所示：（1）小明家离体育场的距离为       km，小明跑步的平均速度为           km/min；（2）当15≤x≤45时，请直接写出y关于x的函数表达式；（3）当小明离家2km时，求他离开家所用的时间．10. （2022龙东中考）为抗击疫情，支援B市，A市某蔬菜公司紧急调运两车蔬菜运往B市．甲、乙两辆货车从A市出发前往B市，乙车行驶途中发生故障原地维修，此时甲车刚好到达B市．甲车卸载蔬菜后立即原路原速返回接应乙车，把乙车的蔬菜装上甲车后立即原路原速又运往B市．乙车维修完毕后立即返回A市．两车离A市的距离y（km）与乙车所用时间x（h）之间的函数图象如图所示．
 （1）甲车速度是_______km/h，乙车出发时速度是_______km/h；（2）求乙车返回过程中，乙车离A市的距离y（km）与乙车所用时间x（h）的函数解析式（不要求写出自变量的取值范围）；（3）乙车出发多少小时，两车之间的距离是120km？请直接写出答案．11. （2022齐齐哈尔中考）在一条笔直的公路上有A、B两地，甲、乙二人同时出发，甲从A地步行匀速前往B地，到达B地后，立刻以原速度沿原路返回A地．乙从B地步行匀速前往A地（甲、乙二人到达A地后均停止运动），甲、乙二人之间的距离y （米）与出发时间x （分钟）之间的函数关系如图所示，请结合图像解答下列问题：（1）A、B两地之间的距离是         米，乙的步行速度是         米/分；（2）图中a=         ，b=         ，c=         ；（3）求线段MN的函数解析式；（4）在乙运动的过程中，何时两人相距80米?（直接写出答案即可）12. （2022牡丹江中考） 2008年5月12日14时28分四川汶川发生里氏8.0级强力地震．某市接到上级通知，立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区．乙组由于要携带一些救灾物资，比甲组迟出发1.25小时（从甲组出发时开始计时）．图中的折线、线段分别表示甲、乙两组的所走路程y甲（千米）、y乙（千米）与时间x（小时）之间的函数关系对应的图象．请根据图象所提供的信息，解决下列问题：（1）由于汽车发生故障，甲组途中停留了___小时；（2）甲组的汽车排除故障后，立即提速赶往灾区．请问甲组的汽车在排除故障时，距出发点的路程是多少千米？（3）为了保证及时联络，甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米，请通过计算说明，按图象所表示的走法是否符合约定？13. （2022绍兴中考）一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x表示进水用时（单位：小时），y表示水位高度（单位：米）．x00.511.52y11.522.53为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择：（），y=ax2+bx+c （），（）．（1）在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．
 （2）当水位高度达到5米时，求进水用时x．14. （2022河南上蔡三模）在同一直线上有甲、乙、丙三地，丙地在甲、乙两地之间．小刚和小强分别从甲、乙两地同时出发，相向而行．小刚匀速行进到丙地后，立即以原速度返回甲地；小强从乙地匀速行进到甲地．在整个行进过程中，他们两人到甲地的距离y（m）与行进的时间x（min）之间的函数关系图象如图所示，请结合图象信息解答下列问题．（1）a＝______，小强的速度为______m/min．（2）求点C的坐标，并说明点C的实际意义．（3）直接写出小刚和小强两人相距200m时小强行进的时间．15. （2022驻马店六校联考三模）某鲜花销售公司每月付给销售人员的工资有两种方案．方案一：没有底薪，只付销售提成；方案二：底薪加销售提成．如图中的射线，射线分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资（单位：元）和（单位：元）与其当月鲜花销售量x（单位：千克）（）的函数关系．（1）分别求﹑与x的函数解析式（解析式也称表达式）；（2）若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过2000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？16. （2022驻马店二模）端午节是我们中华民族的传统节日，某校九年级1班准备在端午节当天组织学生包粽子。班级分为男生（甲）女生（乙）两个小组，甲组男生在包粽子过程中因体育锻炼暂停一会，然后以原来的工作效率继续包粽子，由于时间紧任务重，乙组女生也加入共同加工粽子．设甲组男生加工时间t（分钟），甲组加工粽子的数量为（个），乙组女生加工粽子的数量为（个），其函数图像如图所示．（1）求与t之间的函数关系式，并写出t的取值范围；（2）求a的值，并说明a的实际意义；（3）甲组男生加工多长时间时，甲、乙两组加工粽子的总数为480个？直接写出答案．17. （2022周口川汇区一模）在A、B两地间的一条540km的公路上，甲车从A地匀速开往B地，乙车从B地匀速开往A地，两车同时出发，分别到达目的地后停止．设甲车距A地的路程为y1（km），乙车距A地的路程为y2（km），两车行驶的时间为x（h），y1，y2关于x的函数图象如图所示．（1）填空：y1＝　　；y2＝　　；（2）设甲、乙两车之间的路程为y（km），求y关于x的函数解析式；（3）两车之间的路程不大于450km的时间有多长？18. （2022三门峡二模）某通讯公司就手机流量套餐推出两种方案，如下表： A方案B方案每月基本费用（元）99110每月免费使用流量（G）3040超出后每G收费（元）超过30G后，按照3元/G收费，套外流量使用费用达到50元封顶．超过40G后，超出部分按照5元/G收费．A，B两种方案每月所需费用y（元）与每月使用流量x（G）之间的函数图象如下图所示：（1）请直接写出m，n的值；（2）在方案A中，当每月使用流量超过30G时，求每月所需费用y（元）与每月使用流量（G）之间的函数关系式；（3）结合图象，直接写出在这两种方案中，当每月使用流量x为多少时，选择方案B最划算？19. （2022洛阳一模）某学习小组在数学活动课上设计了一个问题情境．已知林茂的家、体育场、文具店在同一条直线上，林茂从家匀速跑步15min到体育场，在体育场锻炼了一阵后又匀速走到文具店买笔，然后再匀速走回家．给出的图像反映了这个过程中林茂离家的距离ykm与离开家的时间xmin之间的对应关系．请根据相关信息，解答下列问题：（1）填空：①体育场到文具店的距离为______km；②林茂从文具店到家的行进速度为______km/min；③当林茂离家的距离为2km时，他离开家的时间为_____min；（2）当时，请求出y关于x的函数解析式．20. （2022西工大附中三模）世界500强H公司决定购买某演唱会门票奖励部分优秀员工，演唱会的购票方式有以下两种：方式一：若单位赞助广告费10万元，则该单位所购门票的价格为每张0.02万元（其中总费用＝广告赞助费+门票费）；方式二：如图所示设购买门票x张，总费用为y万元（1）求用购票“方式一”时y与x的函数关系式；（2）若H、A两家公司分别采用方式一、方式二购买本场演唱会门票共400张，且A公司购买超过100张，两公司共花费27.2万元，求H、A两公司各购买门票多少张？21. （2022西安交大附中三模）草根医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，根据图象回答下列问题：
 （1）求时，y与x的函数表达式；（2）如果每毫升血液中含药量为3微克及以上时治疗疾病有效．请问病人服药后8小时内有多长时间药物对治疗疾病有效？请说明理由．