2023学年二轮复习解答题专题三十四：抛物线上有关周长问题的探究

这是一份2023学年二轮复习解答题专题三十四：抛物线上有关周长问题的探究，文件包含2023学年二轮复习解答题专题三十四抛物线上有关周长问题的探究原卷版docx、2023学年二轮复习解答题专题三十四抛物线上有关周长问题的探究解析版docx等2份试卷配套教学资源，其中试卷共58页， 欢迎下载使用。
2023学年二轮复习解答题专题三十四：
抛物线上有关周长问题的探究
典例分析
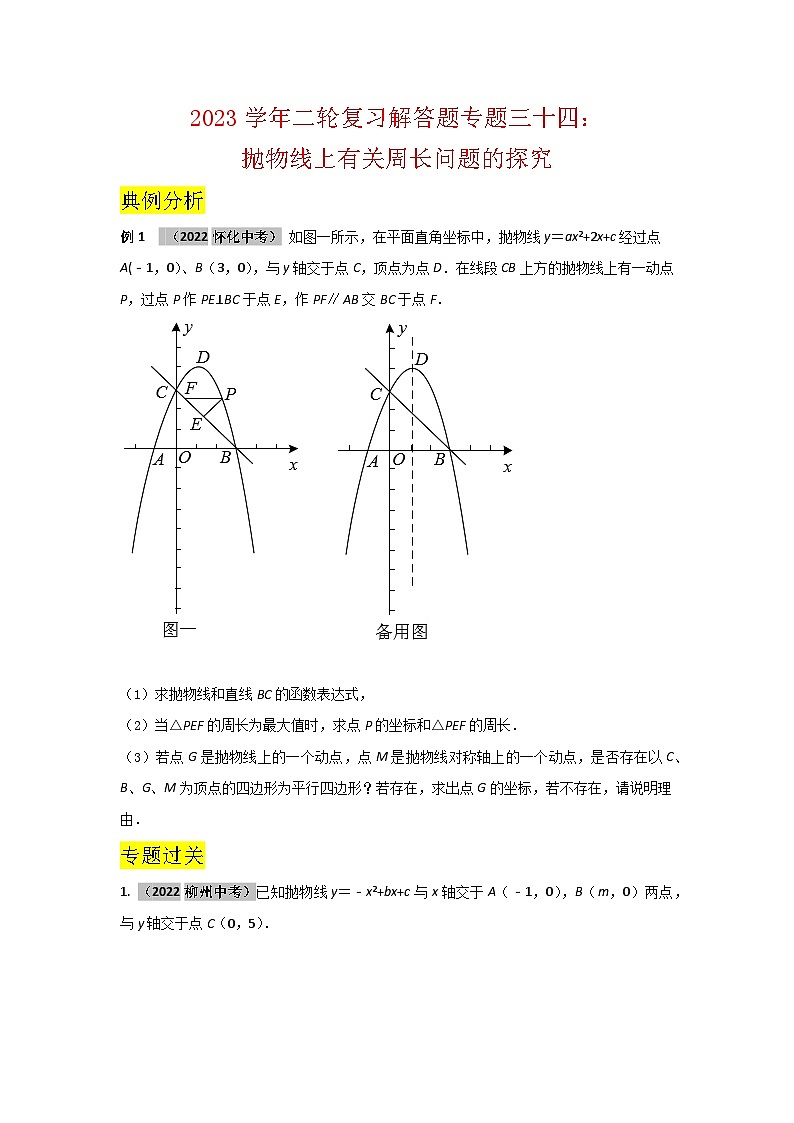
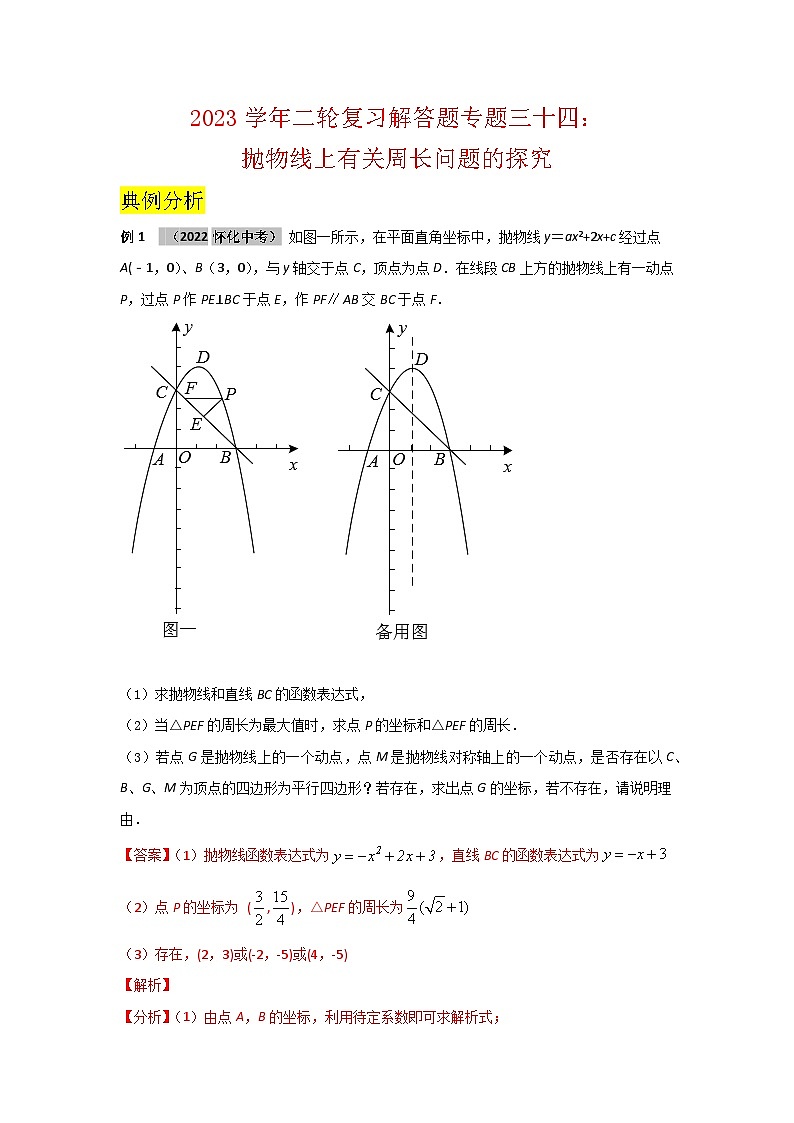
例1 （2022怀化中考） 如图一所示，在平面直角坐标中，抛物线y＝ax2+2x+c经过点A(﹣1，0）、B（3，0），与y轴交于点C，顶点为点D．在线段CB上方的抛物线上有一动点P，过点P作PE⊥BC于点E，作PFAB交BC于点F．


（1）求抛物线和直线BC的函数表达式，
（2）当△PEF的周长为最大值时，求点P的坐标和△PEF的周长．
（3）若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由．
【答案】（1）抛物线函数表达式为，直线BC的函数表达式为
（2）点P的坐标为 (,)，△PEF的周长为
（3）存在，(2，3)或(-2，-5)或(4，-5)
【解析】
【分析】（1）由点A，B的坐标，利用待定系数即可求解析式；
（2）利用直线和抛物线的位置关系相切时对应的等腰直角三角形PEF周长最大，二次函数与一次函数联立方程，根的判别式，从而找出对应点P坐标，进而求出周长；
（3）根据平行四边形对角线性质和中点公式，把BC是否为对角线分情况进行分析，设出点G的横坐标，利用中点公式列方程计算即可求解．
【小问1详解】
解：将点A(-1,0)，B(3,0)代入，得：
，解得 ，
所以抛物线解析式为，C(0，3)
设直线BC的函数表达式 ，将B(3，0)，C(0，3)代入得：
，解得 ，
所以直线BC的函数表达式为
【小问2详解】


解：如图，设将直线BC平移到与抛物线相切时的解析式为 ，与抛物线联立得：
整理得
，解得 ，
将代入，解得，
将代入得，
即△PEF的周长为最大值时，点P的坐标为 (,)
将代入得，
则此时，
因为△PEF为等腰直角三角形，
则△PEF的周长最大为
【小问3详解】
答：存在．
已知B(3，0)，C(0，3)，设点Ｇ(， )，N(1，n)，
当BC为平行四边形对角线时，根据中点公式得： ，，则G点坐标为(2，3)；
当BC为平行四边形对角线时，同样利用中点坐标公式得： 或 ，解得 或 则G点坐标为(-2，-5)或(4，-5)
故点G坐标为(2，3)或(-2，-5)或(4，-5)
【点睛】本题考查了待定系数法求二次函数解析式、二次函数图像上点的坐标特征、待定系数法求一次函数解析式、直线与抛物线的位置关系、根的判别式，等腰直角三角形性质，平行四边形的性质，解题的关键（1）根据点的坐标利用待定系数求解析式；（2利用直线和抛物线的位置关系，巧妙利用判别式；（3）熟悉平行四边形对角线性质，结合中点公式分情况展开讨论．
专题过关
1. （2022柳州中考）已知抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（m，0）两点，与y轴交于点C（0，5）．

（1）求b，c，m的值；
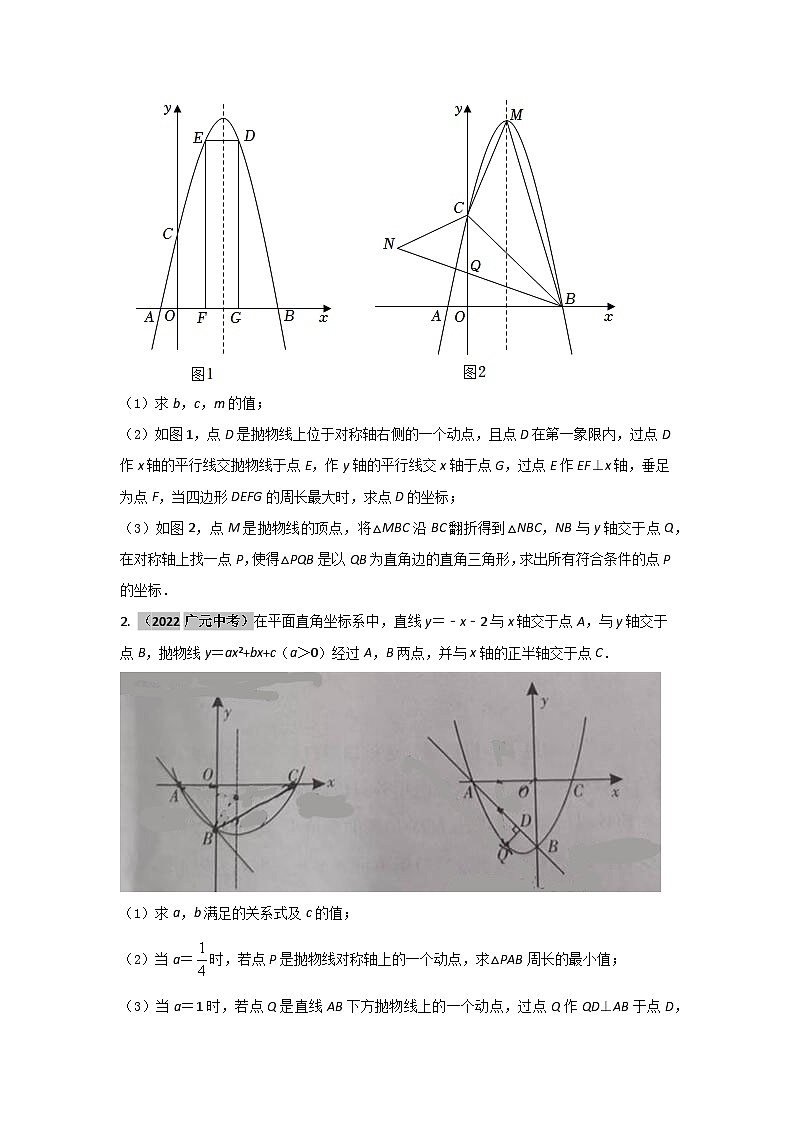
（2）如图1，点D是抛物线上位于对称轴右侧的一个动点，且点D在第一象限内，过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，垂足为点F，当四边形DEFG的周长最大时，求点D的坐标；
（3）如图2，点M是抛物线的顶点，将△MBC沿BC翻折得到△NBC，NB与y轴交于点Q，在对称轴上找一点P，使得△PQB是以QB为直角边的直角三角形，求出所有符合条件的点P的坐标．
【答案】（1）b=4，c=5， m=5
（2）当四边形DEFG的周长最大时，点D的坐标为（3，8）
（3）所有符合条件的点P的坐标为（2，），（2，﹣9）
【解析】
【分析】（1）把A（﹣1，0），C（0，5）代入y＝﹣x2+bx+c，利用待定系数法求解b，c即可，再令y=0，再解方程求解m即可；
（2）先求解抛物线的对称轴为x＝2，设D（x，﹣x2+4x+5），则E（4﹣x，﹣x2+4x+5），证明四边形DEFG是矩形，而 可得四边形DEFG的周长＝2（﹣x2+4x+5）+2（2x﹣4）＝﹣2x2+12x+2＝﹣2（x﹣3）2+20，再利用二次函数的性质可得答案；
（3）过点C作CH⊥对称轴于H，过点N作NK⊥y轴于K，证明△MCH≌△NCK（AAS），再求解N（﹣4，3），求解直线的解析式为： 可得 设P（2，p），再利用勾股定理表示 BP2＝， 再分两种情况建立方程求解即可．
【小问1详解】
把A（﹣1，0），C（0，5）代入y＝﹣x2+bx+c，
，解得：
∴这个抛物线的解析式为：y＝﹣x2+4x+5，
令y＝0，则﹣x2+4x+5＝0，解得x1＝5，x2＝﹣1，
∴B（5，0），
∴m＝5；
【小问2详解】
∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴对称轴为x＝2，
设D（x，﹣x2+4x+5），
∵轴，
∴E（4﹣x，﹣x2+4x+5），
∵过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，
∴四边形DEFG是矩形，
∴
∴四边形DEFG的周长＝2（﹣x2+4x+5）+2（2x﹣4）＝﹣2x2+12x+2＝﹣2（x﹣3）2+20，
∴当x＝3时，四边形DEFG的周长最大，
∴当四边形DEFG的周长最大时，点D的坐标为（3，8）；
【小问3详解】
过点C作CH⊥对称轴于H，过点N作NK⊥y轴于K，

∴∠NKC＝∠MHC＝90°，
由翻折得CN＝CM，∠BCN＝∠BCM，
∵B（5，0），C（0，5）．
∴OB＝OC，
∴∠OCB＝∠OBC＝45°，
∵CH⊥对称轴于H，
∴轴，
∴∠BCH＝45°，
∴∠BCH＝∠OCB，
∴∠NCK＝∠MCH，
∴△MCH≌△NCK（AAS），
∴NK＝MH，CK＝CH，
∵抛物线的解析式为：y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴对称轴为x＝2，M（2，9），
∴MH＝9﹣5＝4，CH＝2，
∴NK＝MH＝4，CK＝CH＝2，
∴N（﹣4，3），
设直线BN的解析式为y＝mx+n，
∴ 解得：
∴直线的解析式为：
∴
设P（2，p），
∴
BP2＝，

分两种情况：
①当∠BQP＝90°时，BP2＝PQ2+BQ2，
∴
解得：
∴
②当∠QBP＝90°时，P′Q2＝BP′2+BQ2，
∴
解得：
∴点P′的坐标为（2，﹣9）．
综上，所有符合条件的点P的坐标为或．
【点睛】本题考查的是利用待定系数法求解二次函数的解析式，二次函数与坐标轴的交点坐标问题，二次函数的性质，对称轴的性质，二次函数与直角三角形，勾股定理的应用，清晰的分类讨论是解本题的关键．
2. （2022广元中考）在平面直角坐标系中，直线y＝﹣x﹣2与x轴交于点A，与y轴交于点B，抛物线y＝ax2+bx+c（a＞0）经过A，B两点，并与x轴的正半轴交于点C．

（1）求a，b满足的关系式及c的值；
（2）当a＝时，若点P是抛物线对称轴上的一个动点，求△PAB周长的最小值；
（3）当a＝1时，若点Q是直线AB下方抛物线上的一个动点，过点Q作QD⊥AB于点D，当QD的值最大时，求此时点Q的坐标及QD的最大值．
【答案】（1）2a=b+1，c=-2；
（2）△PAB周长最小值是2+2；
（3）此时Q（-1，-2），DQ最大值为．
【解析】
【分析】（1）先求得点A、点B的坐标，再利用待定系数法求解即可；
（2）先利用对称性找出△PAB周长最小时点P的位置，此时AP=CP，△PAB的周长最小值为：PB+PA+AB=BC+AB，根据勾股定理求出AB、BC的长即可求出△PAB最小值；
（3）过点Q作QF⊥x轴交于F点，交直线AB于点E，得到∠QED=∠EQD=45°，推出QD=ED=EQ，设Q（t，t2+t-2），E（t，-t-2），求得QE=-t2-2t，再利用二次函数的性质即可求解．
【小问1详解】
解：∵直线y＝﹣x﹣2与x轴交于点A，与y轴交于点B，
∴点A的坐标为(-2，0)，点B的坐标为(0，-2)，
∵抛物线y＝ax2+bx+c（a＞0）经过A，B两点，
∴，
∴2a=b+1，c=-2；
【小问2详解】
解：当a=时，则b=-，
∴抛物线的解析式为y=x2-x-2，
抛物线的对称轴为直线x=1，
∵点A的坐标为(-2，0)，
∴点C的坐标为(4，0) ，

△PAB的周长为：PB+PA+AB，且AB是定值，
∴当PB+PA最小时，△PAB的周长最小，
∵点A、C关于直线x=1对称，
∴连接BC交直线x=1于点P，此时PB+PA值最小，
∵AP=CP，
∴△PAB的周长最小值为：PB+PA+AB=BC+AB，
∵A（-2，0），B（0，-2），C（4，0），
∴OA=2，OB=2，OC=4，
由勾股定理得BC=2，AB=2，
∴△PAB的周长最小值是：2+2．
【小问3详解】
解：当a=1时，b=1，
∴抛物线的解析式为y=x2+x-2，
过点Q作QF⊥x轴交于F点，交直线AB于点E，

∵A（-2，0），B（0，-2），
∴OA=OB，
∴∠OAB=45°，
∵QD⊥AB，
∴∠AEF=∠QED=∠EQD=45°，
∴QD=ED=EQ，
设Q（t，t2+t-2），E（t，-t-2），　
∴QE=-t-2-(t2+t-2)=-t2-2t，
∴DQ=QE=-(t2+2t)= -(t+1)2+，
当t=-1时，DQ有最大值，此时Q（-1，-2）．
【点睛】本题是二次函数的综合题，熟练掌握二次函数的图象及性质，等腰直角三角形的性质是解题的关键．
3. （2022十堰中考） 已知抛物线与轴交于点和点两点，与轴交于点．

（1）求抛物线的解析式；
（2）点是抛物线上一动点（不与点，，重合），作轴，垂足为，连接．
①如图1，若点在第三象限，且，求点的坐标；
②直线交直线于点，当点关于直线的对称点落在轴上时，求四边形的周长．
【答案】（1）
（2）①；②或
【解析】
【分析】（1）把点，代入，即可求解；
（2）①过点C作CQ⊥DP于点Q，可得△CPQ为等腰直角三角形，从而得到PQ=CQ，设点，则OD=-m，，再由四边形OCQD为矩形，可得QC=OD=PQ=-m，DQ=OC=3，从而得到，即可求解；②过点E作EM∥x轴于点M，先求出直线BC的解析式为，证得四边形为菱形，可得，然后根据△CEM∽△CBO，设点，则点，然后分三种情况讨论，即可求解．
【小问1详解】
解：把点，代入得：
，解得：，
∴抛物线解析式为；
【小问2详解】
解：①如图，过点C作CQ⊥DP于点Q，

∵点C（0，-3），
∴OC=3，
∵，
∴△CPQ为等腰直角三角形，
∴CQ=PQ，
设点，则OD=-m，，
∵轴，
∴∠COD=∠ODQ=∠CQD=90°，
∴四边形OCQD为矩形，
∴QC=OD=PQ=-m，DQ=OC=3，
∴，
∴，
解得：或0（舍去），
∴点；
②如图，过点E作EM∥x轴于点M，

令y=0，，
解得：（舍去），
∴点B（-4，0），
∴OB=4，
∴，
设直线BC的解析式为，
把点B（-4，0），C（0，-3）代入得：
，解得：，
∴直线BC解析式为，
∵点关于直线的对称点落在轴上时，
∴，，，
∵DP⊥x轴，
∴PD∥CE′，
∴，
∴，
∴CE=PE，
∴，
∴四边形为菱形，
∵EM∥x轴，
∴△CEM∽△CBO，
∴，
设点， 则点，
当点P在y轴左侧时，EM=-t，
当-4＜t＜0时，，
∴，
∴，
解得：或0（舍去），
∴，
∴四边形的周长为；
当点P在y轴右侧时，EM=-t，
当t≤-4时，，
∴，解得：或0（舍去），
此时，
∴四边形的周长为；
当点P在y轴右侧，即t＞0时，EM=t，，
∴，解得：或0，
不符合题意，舍去；
综上所述，四边形的周长为或．
【点睛】本题主要考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、对称的性质和菱形的判定方法；会利用待定系数法求函数解析式；理解坐标与图形性质；会利用相似比计算线段的长和解一元二次方程是解题的关键．
4.（2021呼伦贝尔中考）如图，直线y＝x+2与抛物线y＝ax2+bx+6（a≠0）相交于点A（，）和点B（4，m）．抛物线与x轴的交点分别为H、K（点H在点K的左侧）．点F在线段AB上运动（不与点A、B重合），过点F作直线FC⊥x轴于点P，交抛物线于点C．
（1）求抛物线的解析式；
（2）如图1，连接AC，是否存在点F，使△FAC是直角三角形？若存在，求出点F的坐标；若不存在，说明理由；
（3）如图2，过点C作CE⊥AB于点E，当△CEF的周长最大时，过点F作任意直线l，把△CEF沿直线l翻折180°，翻折后点C的对应点记为点Q，求出当△CEF的周长最大时，点F的坐标，并直接写出翻折过程中线段KQ的最大值和最小值．
【考点】二次函数综合题．版权所有
【专题】二次函数的应用；推理能力．
【答案】（1）；
（2）存在点 F（3，5）或（，）；
（3）当时，CF最大即△FEC的周长最大，此时F点坐标为，折叠过程中，KQ的最大值为，
KQ的最小值为．
【分析】（1）先把点B代入直线的解析式，求出m的值，再把点A和点B代入抛物线的解析式，即可求出抛物线的解析式；
（2）先设出F的坐标，然后分A为直角顶点和C为直角顶点两种情况，利用等腰直角三角形得性质即可求出点F的坐标；
（3）先设出点C的坐标，再设出点F的坐标，然后表示出三角形CEF的周长，求出周长取最大值时点C和F的坐标即可，折叠过程中，当K，F，Q共线，且K和Q在F两侧时，KQ的最大，K和Q在F同侧时，KQ的最小．
【解答】解：（1）∵直线y＝x+2过点B（4，m），
∴m＝4+2，
解得m＝6，
∴B（4，6），
把点A和B代入抛物线的解析式，得：
，
解得，
∴抛物线的解析式为；
（2）存在点F，使△FAC为直角三角形，
设F（n，n+2），直线AB与x轴交与M，则M（﹣2，0），直线AB与y轴交与点N，则N（0，2），

∵FC∥y轴，
∴C（n，2n2﹣8n+6），
∵直线y＝x+2与x轴的交点为M（﹣2，0），与y轴交点为N（0，2），
∴OM＝ON＝2，
∴∠ONM＝45°，
∵FC∥y轴，
∴∠AFC＝∠ONM＝45°，
若△FAC为直角三角形，则分两种情况讨论：
（i）若点A为直角顶点，即∠FAC＝90°，
过点A作AD⊥FC于点D，
在Rt△FAC中，
∵∠AFC＝45°，
∴AF＝AC，
∴DF＝DC，
∴AD＝FC，
∵n＝，
化简得：2n2﹣7n+3＝0，
解得：n1＝3，（与A重合舍去），
∴F（3，5），
（ii）若点C为直角顶点，即∠FCA＝90°，则AC∥x轴，

在Rt△FAC中，
∵∠AFC＝45°，
∴AC＝CF，
∴n＝（n+2）﹣（2n2﹣8n+6，
化简得：4n2﹣16n+7＝0，
解得：，（舍去），
∴F（，），
综上所述：存在点 F（3，5）或（，），使△FAC为直角三角形；
（3）设F（c，c+2），
∵FC∥y轴，
∴C（c，2c2﹣8c+6），

在Rt△FEC中，
∵∠AFC＝45
∴EF＝EC＝CF•sin∠AFC＝，
∴当CF最大时，△FEC的周长最大，
∵CF＝（c+2）﹣（2c2﹣8c+6）＝﹣2c2+9c﹣4＝，
又∵﹣2＜0，
∴当时，CF最大即△FEC的周长最大，此时F点坐标为，
折叠过程中，当K，F，Q共线，且K和Q在F两侧时，KQ的最大，K和Q在F同侧时，KQ的最小，
∵CF＝，
由（1）知点K的坐标为（3，0），
∴KF＝，
∴KQ的最大值为CF+KF＝，KQ的最小值为CF﹣KF＝．
5. （2021遂宁中考）如图，已知二次函数的图象与x轴交于A和B（－3，0）两点，与y轴交于C（0，－3），对称轴为直线，直线y＝－2x＋m经过点A，且与y轴交于点D，与抛物线交于点E，与对称轴交于点F．
（1）求抛物线的解析式和m的值；
（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；
（3）直线y＝1上有M、N两点（M在N的左侧），且MN＝2，若将线段MN在直线y＝1上平移，当它移动到某一位置时，四边形MEFN的周长会达到最小，请求出周长的最小值（结果保留根号）．

【答案】（1）；m=2；（2）存在，或；（3）
【解析】
【分析】（1）根据抛物线的对称性求出A（1，0），再利用待定系数法，即可求解；再把点A坐标代入直线的解析式，即可求出m的值；
（2）先求出E（-5，12），过点E作EP⊥y轴于点P，从而得，即可得到P的坐标，过点E作，交y轴于点，可得，再利用tan∠ADO=tan∠PE，即可求解；
（3）作直线y=1，将点F向左平移2个单位得到，作点E关于y=1的对称点，连接与直线y=1交于点M，过点F作FN∥，交直线y=1于点N，在中和 中分别求出EF， ，进而即可求解．
【详解】（1）解：∵二次函数的图象与x轴交于A和B（－3，0）两点，对称轴为直线，
∴A（1，0），
设二次函数解析式为：y=a(x-1)(x+3)，把C（0，－3）代入得：-3=a(0-1)(0+3)，解得：a=1，
∴二次函数解析式为：y= (x-1)(x+3)，即：，
∵直线y＝－2x＋m经过点A，
∴0=-2×1+m，解得：m=2；
（2）由（1）得：直线AF的解析式为：y=-2x+2，
又∵直线y=-2x+2与y轴交于点D，与抛物线交于点E，
∴当x=0时，y=2，即D（0，2），
联立，解得：，，
∵点E在第二象限，
∴E（-5，12），
过点E作EP⊥y轴于点P，

∵∠ADO=∠EDP，∠DOA=∠DPE=90°，
∴，
∴P（0，12）；
过点E作，交y轴于点，可得，
∵∠ED+∠PED=∠PE+∠PED=90°，
∴∠ADO=∠ED=∠PE，即：tan∠ADO=tan∠PE，
∴，即：，解得：，
∴（0，14.5），
综上所述：点P坐标为（0，12）或（0，14.5）；
（3）∵点E、F均为定点，
∴线段EF长定值，
∵MN=2，
∴当EM+FN为最小值时，四边形MEFN的周长最小，
作直线y=1，将点F向左平移2个单位得到，作点E关于y=1的对称点，连接与直线y=1交于点M，过点F作FN∥，交直线y=1于点N，

由作图可知：，
又∵三点共线，
∴EM+FN=，此时，EM+FN的值最小，
∵点F为直线y=-2x+2与直线x=-1的交点，
∴F（-1，4），
∴（-3，4），
又∵E（-5，12），
∴（-5，-10），
延长F交线段E于点W，
∵F与直线y=1平行，
∴FW⊥E，
∵在中，由勾股定理得：EF=，
在中，由勾股定理得：=，
∴四边形MEFN的周长最小值=ME+FN+EF+MN=．
【点睛】本题主要考查二次函数与平面几何的综合，掌握待定系数法，相似三角形的判定和性质，添加辅助线，利用轴对称图形的性质，构造线段和的最小值，是解题的关键．
6. （2021重庆中考A卷）如图，在平面直角坐标系中，抛物线经过A（0，﹣1），B（4，1）．直线AB交x轴于点C，P是直线AB下方抛物线上的一个动点．过点P作PD⊥AB，垂足为D，PE∥x轴，交AB于点E．

（1）求抛物线的函数表达式；
（2）当△PDE的周长取得最大值时，求点P的坐标和△PDE周长的最大值；
（3）把抛物线平移，使得新抛物线的顶点为（2）中求得的点P．M是新抛物线上一点，N是新抛物线对称轴上一点，直接写出所有使得以点A，B，M，N为顶点的四边形是平行四边形的点M的坐标，并把求其中一个点M的坐标的过程写出来．
【答案】（1）；（2）t=2时，△PDE周长取得最大值，最大值为， 点P的坐标为（2，﹣4）；（3）满足条件的点M的坐标有（2，﹣4），（6，12），（﹣2，12），过程见解析
【解析】
分析】（1）利用待定系数法求函数表达式即可；
（2）先求出直线AB的函数表达式和点C坐标，设P，其中0