2023学年二轮复习解答题专题三十八：抛物线上旋转问题的探究

这是一份2023学年二轮复习解答题专题三十八：抛物线上旋转问题的探究，文件包含2023学年二轮复习解答题专题三十八抛物线上旋转问题的探究原卷版docx、2023学年二轮复习解答题专题三十八抛物线上旋转问题的探究解析版docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。
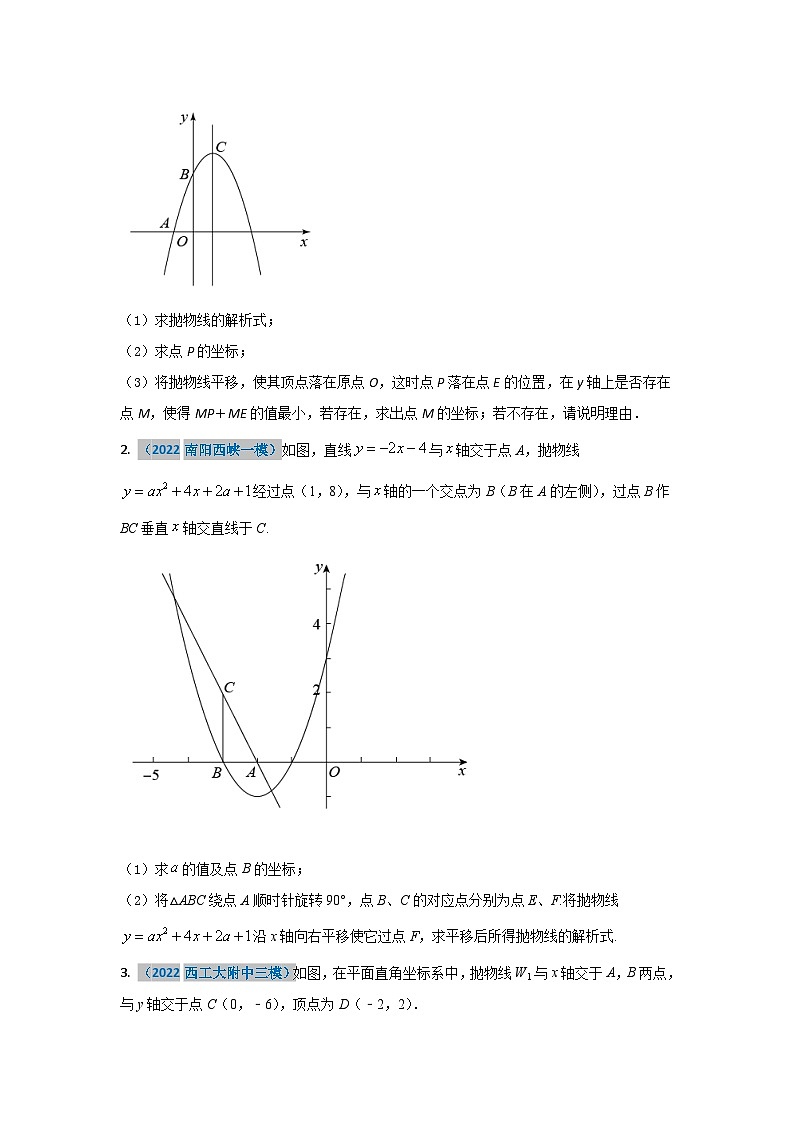
2023学年二轮复习解答题专题三十八：抛物线上旋转问题的探究典例分析例1  （2022梧州中考） 如图，在平面直角坐标系中，直线分别与x，y轴交于点A，B，抛物线恰好经过这两点．（1）求此抛物线的解析式；（2）若点C的坐标是，将绕着点C逆时针旋转90°得到，点A的对应点是点E．①写出点E的坐标，并判断点E是否在此抛物线上；②若点P是y轴上的任一点，求取最小值时，点P的坐标．【答案】（1）    （2）①点E在抛物线上；②（0，）【解析】【分析】（1）先求出A、B坐标，然后根据待定系数法求解即可；（2）①根据旋转性质求出EF=AO=3，CF=CO=6，从而可求E的坐标，然后把E的坐标代入（1）的函数解析式中，从而判断出点E是否在抛物线上；②过点P作PQ⊥AB于Q，证明△ABO∽△PBQ，从而求出，则可判断当P，E，Q三点共线，且EP⊥AB时，取最小值，然后根据待定系数法求直线EP解析式，即可求出点P的坐标．【小问1详解】解：当x=0时，y=-4，当y=0时，，∴x=-3，∴A（-3，0），B（0，-4），把A、B代入抛物线，得，∴，∴抛物线解析式为；【小问2详解】①∵A（-3，0），C（0，6），∴AO=3，CO=6，由旋转知：EF=AO=3，CF=CO=6，∠FCO=90°∴E到x轴的距离为6-3=3，∴点E的坐标为（6，3），当x=3时，，∴点E在抛物线上；②过点P作PQ⊥AB于Q，又∠AOB=90°，∴∠AOB=∠PQB，在Rt△ABO中，AO=3，BO=4，∴由勾股定理得：AB=5，∵∠AOB=∠PQB，∠ABO=∠PBQ，∴△ABO∽△PBQ，∴，∴，∴，∴，∴当P，E，Q三点共线，且EP⊥AB时，取最小值，∵EP⊥AB，∴设直线EP解析式为，又E（6，0），∴，∴，∴直线EP解析式为，当x=0时，y=，∴点P坐标为（0，）．【点睛】本题考查了待定系数法求二次函数函数解析式，相似三角形的判定与性质等，解第（2）题第②问的关键是正确作出点P的位置．专题过关1. （2022凉山中考） 在平面直角坐标系xoy中，已知抛物线y＝－x2＋bx＋c经过点A（－1，0）和点B（0，3），顶点为C，点D在其对称轴上，且位于点C下方，将线段DC绕点D按顺时针方向旋转90°，点C落在抛物线上的点P处．（1）求抛物线的解析式；（2）求点P的坐标；（3）将抛物线平移，使其顶点落在原点O，这时点P落在点E的位置，在y轴上是否存在点M，使得MP＋ME的值最小，若存在，求出点M的坐标；若不存在，请说明理由．【答案】（1）    （2）    （3）存在，【解析】【分析】（1）根据点的坐标，利用待定系数法即可得；（2）先求出抛物线的对称轴，再设点的坐标为，则，根据旋转的性质可得，从而可得，将点代入抛物线的解析式求出的值，由此即可得；（3）先根据点坐标的平移规律求出点，作点关于轴的对称点，连接，从而可得与轴的交点即为所求的点，再利用待定系数法求出直线的解析式，由此即可得出答案．【小问1详解】解：将点代入得：，解得，则抛物线的解析式为．【小问2详解】解：抛物线的对称轴为直线，其顶点的坐标为，设点的坐标为，则，由旋转的性质得：，，即，将点代入得：，解得或（舍去），当时，，所以点的坐标为．【小问3详解】解：抛物线的顶点的坐标为，则将其先向左平移1个单位长度，再向下平移4个单位长度恰好落在原点，这时点落在点的位置，且，，即，恰好在对称轴直线上，如图，作点关于轴的对称点，连接，则，由两点之间线段最短可知，与轴的交点即为所求的点，此时的值最小，即的值最小，由轴对称的性质得：，设直线的解析式为，将点代入得：，解得，则直线的解析式为，当时，，故在轴上存在点，使得的值最小，此时点的坐标为．【点睛】本题考查了求二次函数的解析式、二次函数的图象与性质、旋转的性质、点坐标的平移规律等知识点，熟练掌握待定系数法和二次函数的图象与性质是解题关键． 2. （2022南阳西峡一模）如图，直线与轴交于点A，抛物线经过点（1，8），与轴的一个交点为B（B在A的左侧），过点B作BC垂直轴交直线于C.
 （1）求的值及点B的坐标；（2）将△ABC绕点A顺时针旋转90°，点B、C的对应点分别为点E、F.将抛物线沿x轴向右平移使它过点F，求平移后所得抛物线的解析式.【答案】（1）a=1，B(-3，0)    （2）3#【解析】【分析】(1)把已知坐标代入解析式，得到8=a+4+2a+1，求得a值，回代a值，得到抛物线的解析式，求得抛物线与x轴的交点坐标，根据直线解析式确定A的坐标，根据已知即确定B的坐标．(2)根据旋转性质，得到F(0，1)，设抛物线向右平移m个单位，解析式为，把点F坐标代入解析式求解即可．【小问1详解】∵直线与轴交于点A，抛物线经过点（1，8），∴A(-2，0)，8=a+4+2a+1，解得a=1；∴抛物线解析式为，∴，∴，解得，，∵与轴的一个交点为B（B在A的左侧），∴B(-3，0)．【小问2详解】∵B(-3，0)，直线，∴C(-3，2)，∴AB=1，BC=2，OA=2，根据旋转性质，得AE=AB=1，EF=BC=2，AC=AF，∠CAF=90°，连接OF，∴∠FAO+∠BAC =90°，BC=OA，∵∠BCA+∠BAC =90°，∴∠FAO=∠ACB，∴△FAO≌△ACB，∴FO=1，∠AOF=∠CBA =90°，
 ∴点F在x轴的正半轴，∴点F(0，1)，∵，设抛物线向右平移了m个单位后经过点F，∴过点F(0，1)，∴，解得m=或m=，∴抛物线的解析式为3或．【点睛】本题考查了抛物线与一次函数的综合，待定系数法确定解析式，抛物线与轴的交点，旋转的性质，函数的平移，三角形全等，熟练掌握抛物线的平移，抛物线与x轴交点问题是解题的关键．3. （2022西工大附中三模）如图，在平面直角坐标系中，抛物线W1与x轴交于A，B两点，与y轴交于点C（0，﹣6），顶点为D（﹣2，2）．
 （1）求抛物线W1表达式；（2）将抛物线W1绕原点O旋转180°得到抛物线W2，抛物线W2的顶点为D'，在抛物线W2上是否存在点M，使S△D′AD＝S△D′DM？若存在，请求出点M的坐标；若不存在，请说明理由．【答案】（1）    （2）存在，【解析】【分析】（1）表示出顶点式，将点代入即可；（2）由题意求得抛物线W2的顶点坐标和解析式，在坐标系中画出抛物线W2的图象，利用S△DAD′＝S△ADO+S△AOD′求出三角形DD′A的面积；设，过点M作轴交于点N，表示出MN，列方程求解即可．【小问1详解】解：，设抛物线的表达式为：，将点代入得：，解得：，，【小问2详解】解：，， ，连接， ，，，
 设，过点M作轴交于点N，，，，，，，，，，．【点睛】本题主要考查了抛物线与x轴的交点，二次函数的性质，二次函数图象上点的坐标的特征，待定系数法确定二次函数的解析式，二次函数图象与几何变换，利用点的坐标表示出相应线段的长度是解题的关键．4．（2021达州中考）（11分）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c交x轴于点A和C（1，0），交y轴于点B（0，3），抛物线的对称轴交x轴于点E，交抛物线于点F．（1）求抛物线的解析式；（2）将线段OE绕着点O沿顺时针方向旋转得到线段OE'，旋转角为α（0°＜α＜90°），连接AE′，BE′，求BE′+AE′的最小值；（3）M为平面直角坐标系中一点，在抛物线上是否存在一点N，使得以A，B，M，N为顶点的四边形为矩形？若存在，请直接写出点N的横坐标；若不存在，请说明理由．【解答】解：（1）把C（1，0），B（0，3）代入y＝﹣x2+bx+c中，得：，∴b＝﹣2，c＝3，∴y＝﹣x2﹣2x+3，（2）在OE上取一点D，使得OD＝OE，连接AE'，BD，∵，对称轴x＝﹣1，∴E（﹣1，0），OE＝1，∴OE'＝OE＝1，OA＝3，∴，又∵∠DOE'＝∠E'OA，△DOE'∽△E'OA，∴，∴，当B，E'，D三点共线时，BE′+DE′最小为BD，BD＝＝，∴的最小值为；（3）∵A（﹣3，0），B（0，3），设N（n，﹣n2﹣2n+3），M（x，y），则AB2＝18，AN2＝（n2+2n﹣3）2+（n+3）2，BN2＝n2+（n2+2n）2，∵ABMN构成的四边形是矩形，∴△ABN是直角三角形，若AB是斜边，则AB2＝AN2+BN2，即18＝（n2+2n﹣3）2+（n+3）2+n2+（n2+2n）2，解得：n1＝，，∴N的横坐标为或，若AN是斜边，则AN2＝AB2+BN2，即（n2+2n﹣3）2+（n+3）2＝18+（n2+2n）2，解得n＝﹣1，∴N的横坐标是﹣1，若BN是斜边，则BN2＝AB2+AN2，即n2+（n2+2n）2＝18+（n2+2n﹣3）2+（n+3）2，解得n＝2，∴N的横坐标为2，综上N的横坐标为，，﹣1，2．