新高考数学二轮复习课件专题八 8.4 直线、平面垂直的判定和性质（含解析）

这是一份新高考数学二轮复习课件专题八 8.4 直线、平面垂直的判定和性质（含解析），共17页。PPT课件主要包含了线面垂直的性质，面面垂直的性质等内容，欢迎下载使用。

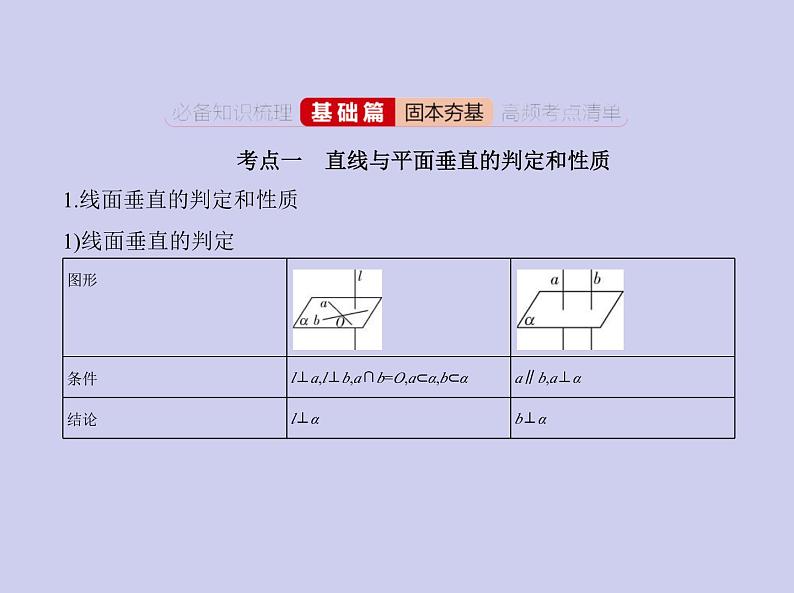
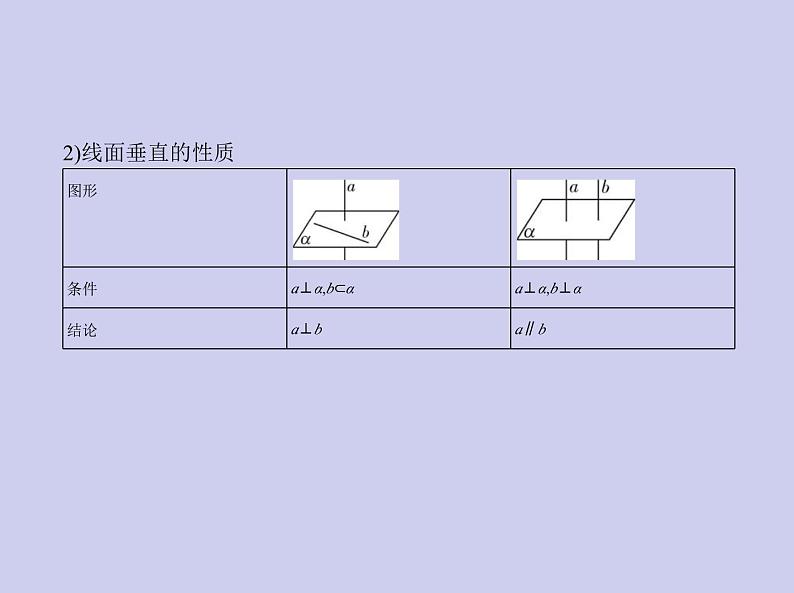
考点一　直线与平面垂直的判定和性质1.线面垂直的判定和性质1)线面垂直的判定
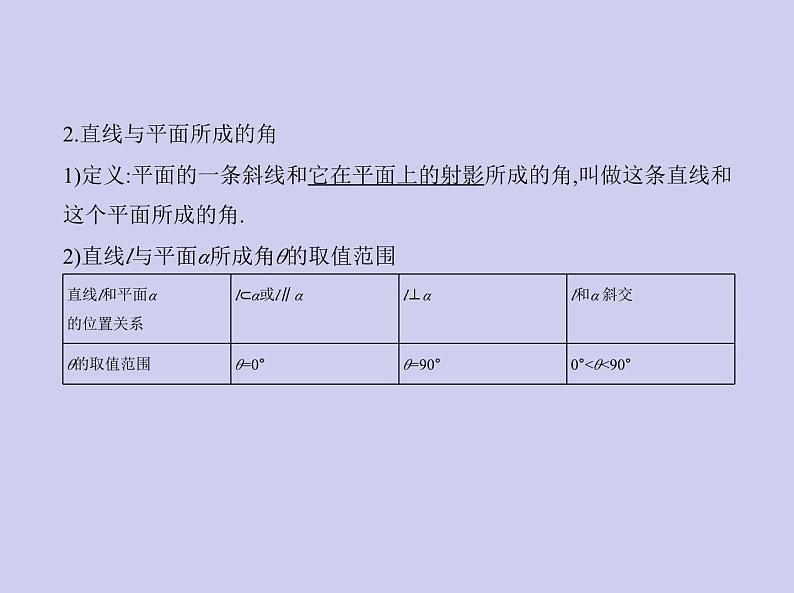
2.直线与平面所成的角1)定义:平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和 这个平面所成的角.2)直线l与平面α所成角θ的取值范围
3)最小角定理:平面的斜线和它在平面内的射影所成的角是这条斜线和 这个平面内任一条直线所成角中最小的角.三余弦公式:cs θ=cs θ1·cs θ2(如图所示,其中θ1是斜线OA与平面α所成的 角,θ2是斜线OA的射影AB与平面内的直线AC的夹角,θ是斜线OA与平面内 的直线AC的夹角).
考点二　平面与平面垂直的判定和性质1.二面角1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角.2)二面角的平面角在二面角的棱上任取一点,以此点为垂足,在两个半平面内分别作垂直于 棱的两条射线,这两条射线所组成的角叫做二面角的平面角.记此角为θ, 当θ=90°时,二面角叫做直二面角.3)二面角的取值范围:[0,π].
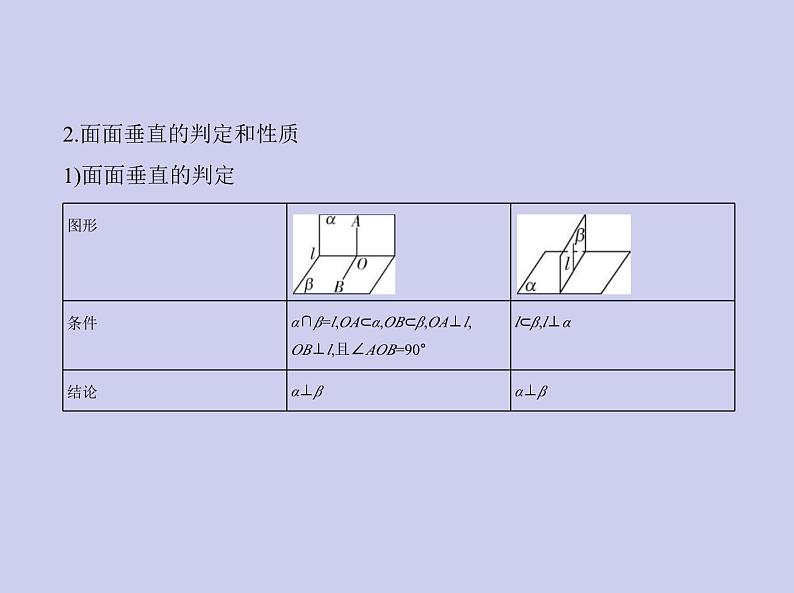
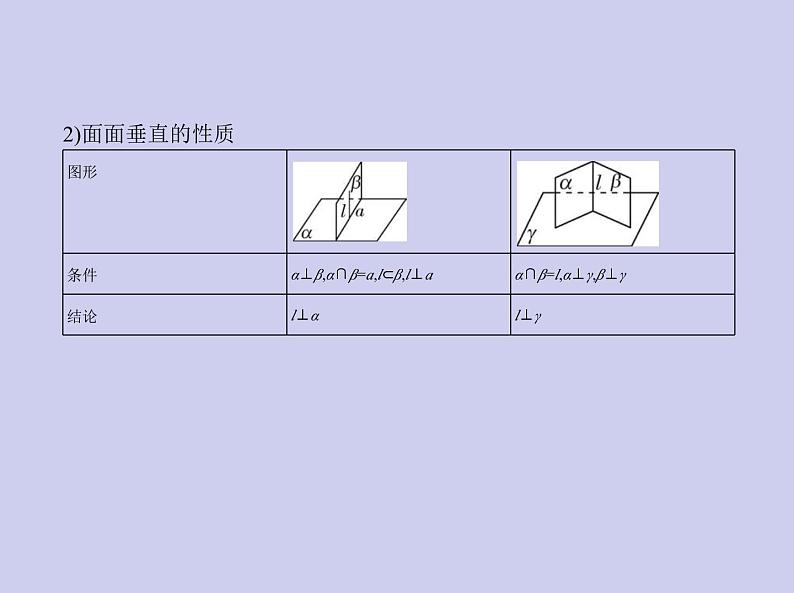
2.面面垂直的判定和性质1)面面垂直的判定
【知识拓展】 1.三垂线定理及其逆定理1)三垂线定理:在平面内的一条直线,如果与这个平面的一条斜线在这个 平面内的射影垂直,那么它也与这条斜线垂直.2)三垂线定理的逆定理:如果平面内一条直线与该平面的一条斜线垂直, 那么这条直线也垂直于这条斜线在平面内的射影.2.垂直问题的转化方向图 
考法一　判断或证明直线与平面垂直的方法1.利用线面垂直的判定定理:l⊥a,l⊥b,a∩b=O,a⊂α,b⊂α⇒l⊥α(主要方 法);2.利用平行线垂直平面的传递性:a∥b,a⊥α⇒b⊥α;3.利用面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β(主要方法);4.利用面面平行的性质:α∥β,a⊥β⇒a⊥α;5.利用面面垂直的性质:α⊥β,α⊥γ,β∩γ=l⇒l⊥α.
例1 (2018课标Ⅱ,19,12分)如图,在三棱锥P-ABC中,AB=BC=2 ,PA=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且MC=2MB,求点C到平面POM的距离.
由OP2+OB2=PB2知,OP⊥OB.由OP⊥OB,OP⊥AC,OB∩AC=O知PO⊥平面 ABC.(2)作CH⊥OM,垂足为H.由(1)可得OP⊥CH,又OP∩OM=O,所以CH⊥平 面POM.故CH的长为点C到平面POM的距离.由题设可知OC= AC=2,CM= BC= ,∠ACB=45°.所以OM= ,CH= = .所以点C到平面POM的距离为 .
考法二　判断或证明平面与平面垂直的方法1.利用面面垂直的判定定理:l⊥α,l⊂β⇒α⊥β(主要方法);2.利用面面垂直的定义(作出两平面构成的二面角的平面角,并计算其大 小为90°);3.利用平行的传递性:α∥β,α⊥γ⇒β⊥γ.
解析 (1)证明:由于PD⊥平面ABCD,AM⊂平面ABCD,则PD⊥AM,又PB⊥ AM,PB∩PD=P,PB,PD⊂平面PBD,所以AM⊥平面PBD,因为AM⊂平面 PAM,所以平面PAM⊥平面PBD.(2)由(1)知AM⊥平面PBD,因为BD⊂平面PBD,所以AM⊥BD,所以∠MAB +∠ABD=90°,因为四边形ABCD为矩形,所以∠DAB=∠ABM,所以∠MAB +∠AMB=90°,所以∠ABD=∠AMB,则△DAB∽△ABM,则 = ,又AB=DC=1,M为BC的中点,∴AD= ,∴S矩形ABCD=AB·AD= ,∴V四棱锥P-ABCD= S矩形ABCD·PD= × ×1= .
考法三　翻折问题的处理方法解决立体几何中的翻折问题,关键是搞清楚翻折前后图形中的位置关系 和数量关系的变化情况,以及翻折过程中运动变化的点的位置.一般地,位 于“折痕”同侧的点、线、面之间的位置关系和数量关系不变,而位于 “折痕”两侧的点、线、面之间的位置关系会发生变化.对于不变的关 系一般在平面图形中处理,而对于变化的关系则在立体图形中解决.
例3 (2021成都摸底测试,19)如图①,在菱形ABCD中,∠A=60°且AB=2,E为 AD的中点.将△ABE沿BE折起到△A'BE的位置,使A'D= ,得到如图②所示的四棱锥A'-BCDE.(1)求证:平面A'BE⊥平面A'BC;(2)若P为A'C的中点,求三棱锥P-A'BD的体积.