
浙江省绍兴市诸暨市2022-2023学年高一技术下学期6月期末试题(Word版附解析)
展开第一部分 信息技术(共50分)
一、选择题(本大题共12小题,每小题2分,共24分。每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)
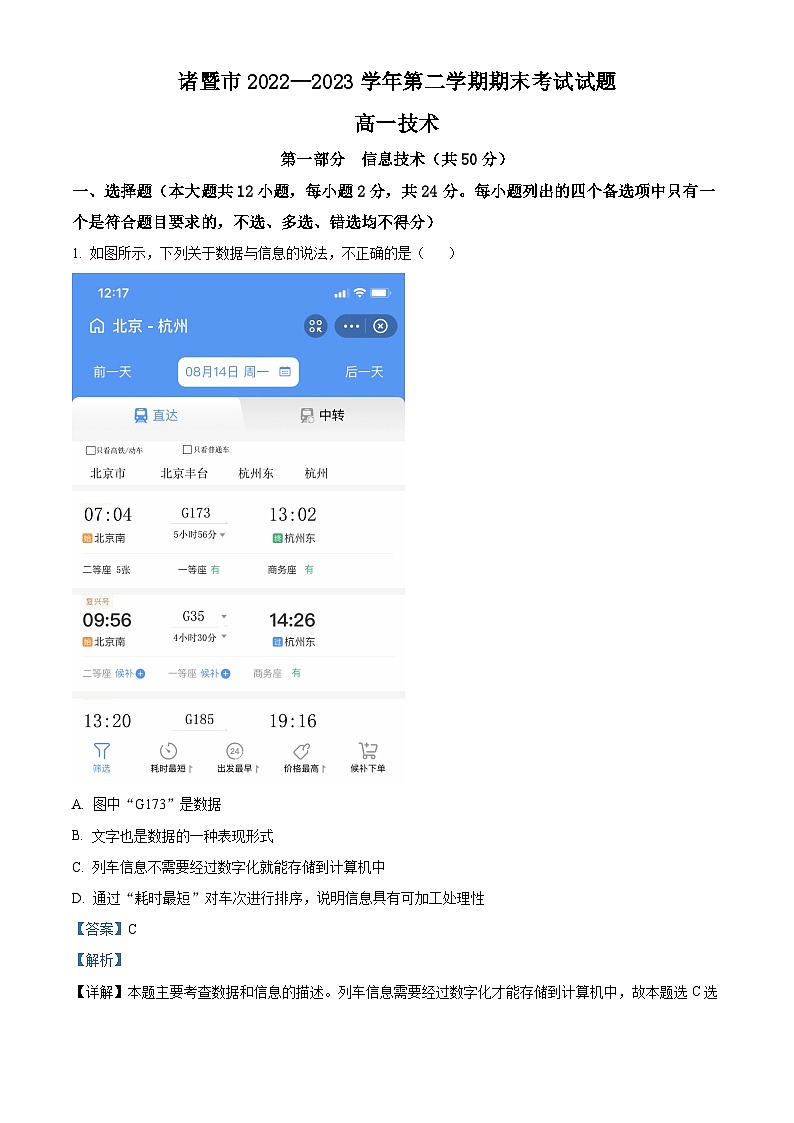
1. 如图所示,下列关于数据与信息的说法,不正确的是( )
A. 图中“G173”是数据
B. 文字也是数据的一种表现形式
C. 列车信息不需要经过数字化就能存储到计算机中
D. 通过“耗时最短”对车次进行排序,说明信息具有可加工处理性
【答案】C
【解析】
【详解】本题主要考查数据和信息的描述。列车信息需要经过数字化才能存储到计算机中,故本题选C选项。
2. 下列关于数字化和编码的说法正确的是( )
A. 二维码与条形码相比,能存储更多信息
B. 数字化是将数字信号转化为模拟信号的过程
C. 汉字在计算机内使用汉字交换码来表示,不使用二进制编码
D. 若某音频文件的量化位数为4位,则其量化值取值范围为0~3
【答案】A
【解析】
【详解】本题考查的是数字化和编码相关知识。二维码与条形码相比,能存储更多的信息,选项A说法正确;数字化是将模拟信号转化为数字信号的过程,选项B说法错误;汉字在计算机内二进制编码,选项C说法错误;若某音频文件的量化位数为4位,则其量化值取值范围为0~15,选项D说法错误。故本题应选A。
3. 近年来网络诈骗层出不穷,为保护个人信息和财产安全,下列行为正确是( )
A. 养成定期更改账号密码的习惯
B. 在手机上打开中奖短信链接
C. 百度搜索金融软件,下载安装并充值投资
D. 收集朋友微信、QQ、手机号码发布到网上售卖
【答案】A
【解析】
【详解】本题考查的是信息安全。养成定期更改账号密码的习惯,可以保护个人信息和财产安全,选项A正确;不要随意点击陌生的链接,故选项B做法错误;不要随意安装陌生软件,故选项C做法错误;微信、QQ、手机号码属于个人敏感信息,不得发布到网上售卖,选项D做法错误。故本题应选A。
4. 下列关于大数据的说法,正确的是( )
A. 大数据要分析的是全体数据,每一个数据都必须准确
B. 大数据指数据量庞大、价值密度高的数据
C. 大数据应用不会泄露用户隐私信息
D. 一般采用分治思想进行大数据分析
【答案】D
【解析】
【详解】本题考查的是大数据相关知识。大数据要分析的是全体数据,但并不要求每一个数据都必须准确,选项A说法错误;大数据指数据量庞大、价值密度低的数据,选项B说法错误;大数据应用会泄露用户隐私信息,选项C说法错误;一般采用分治思想进行大数据分析,选项D说法正确。
5. 下列关于文本数据处理描述不正确的是( )
A. 文本数据处理主要应用在搜索引擎、情报分析、自动摘要、自动校对、自动应答等方面
B. 基于词典的分词方法、基于统计的分词方法和基于规则的分词方法是常用的中文分词算法,其中基于规则的统计方法在实际应用中较多
C. 标签云用词频表现文本特征,将关键词按照一定的顺序和规律排列,并以文字大小的形式代表词语的重要性
D. 典型的中文文本处理过程主要包括:分词、特征提取、数据分析、结果呈现等
【答案】B
【解析】
【详解】本题主要考查文本数据处理。文本数据处理主要应用在搜索引擎、情报分析、自动摘要、自动校对、自动应答等方面;基于规则的分词是一种机械分词方法,需要不断更新和维护词典,并未在实际中广泛应用;标签云用词频表现文本特征,将关键词按照一定的顺序和规律排列,并以文字大小的形式代表词语的重要性;典型的中文文本处理过程主要包括:分词、特征提取、数据分析、结果呈现等,故本题选B选项。
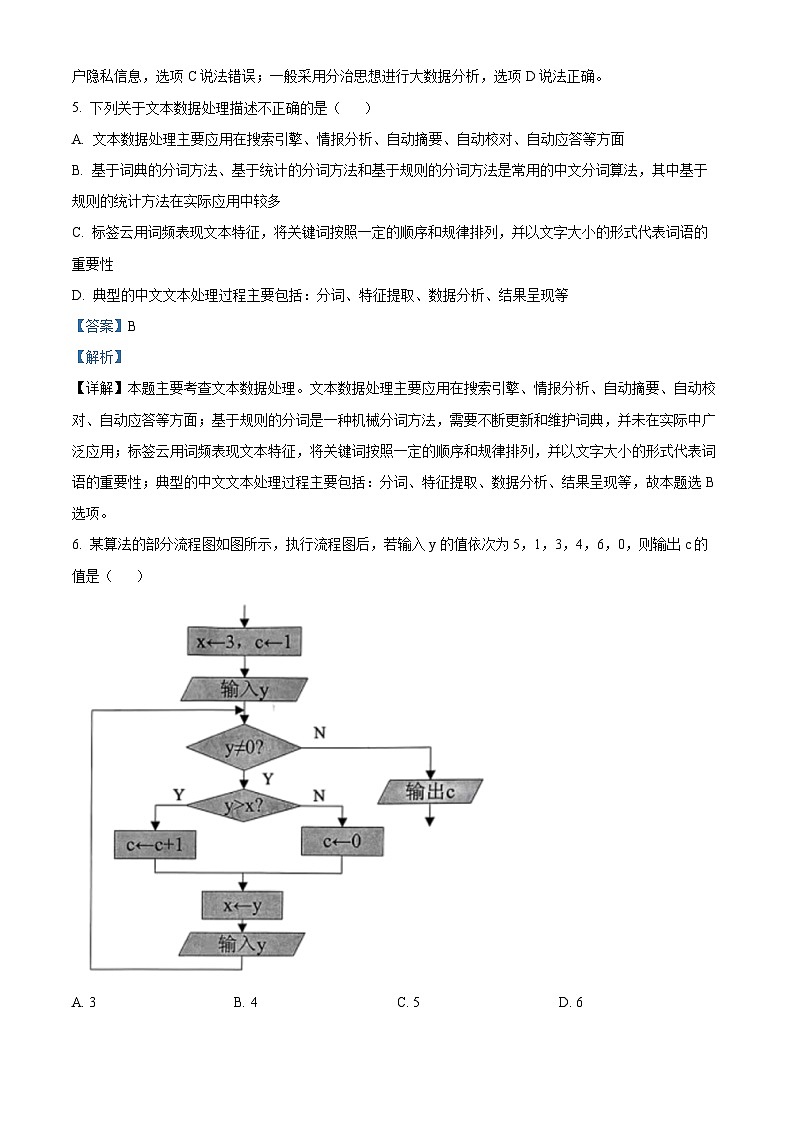
6. 某算法的部分流程图如图所示,执行流程图后,若输入y的值依次为5,1,3,4,6,0,则输出c的值是( )
A. 3B. 4C. 5D. 6
【答案】A
【解析】
【详解】本题考查的是流程图识读。阅读流程图可知c是统计最后一段输入值比前一个值大的个数,3>1,4>3,6>4。3个,故本题应选A。
7. 下列关于算法的描述,正确的是( )
A. 算法中可以包含无限循环,所以算法的执行步骤可以是无限的
B. 算法的控制结构有顺序、选择、循环和树形结构
C. 一个完整的算法可以没有输入,必须要有输出
D. 算法只能用流程图表示
【答案】C
【解析】
【详解】本题主要考查算法的描述。算法的执行步骤必须是有限的;算法的控制结构有顺序、选择和循环结构;一个完整的算法可以没有输入,必须要有输出;算法能用流程图、自然语言等表示,故本题选C选项。
8. 下列Pythn表达式中,值最小的是( )
A. 2022//10%7B. len(“Fyms6S!”)C. abs(-7)D. 66/10
【答案】A
【解析】
【详解】本题考查的是Pythn表达式。2022//10%7=6,len("Fyms6S!")=7,abs(-7)=7,66/10=6.6,故本题应选A。
9. 字符串s的值为 'the quick brwn fx jumps ver a lazy dg',则下列说法正确的是( )
A. s[1]的值为't'B. s[-1:-4:-1]的值为'gd'
C. s[0:2]值为'the'D. s[: :]的值为''
【答案】B
【解析】
【详解】本题主要考查字符串的操作。字符串的下标从0开始,s[1]的值为'h';切片操作基本表达式:bject[start_index:end_index:step],step:正负数均可,其绝对值大小决定了切取数据时的“步长”,而正负号决定了“切取方向”,正表示“从左往右”取值,负表示“从右往左”取值。start_index:表示起始索引(包含该索引对应值),该参数省略时,表示从对象“端点”开始取值。end_index:表示终止索引(不包含该索引对应值),该参数省略时,表示一直取到数据“端点”。s[-1:-4:-1]的值为'gd',s[0:2]的值为'th',s[: :]的值为 'the quick brwn fx jumps ver a lazy dg',故本题选B选项。
10. 有下面一段程序:
p=[2,1,3,4,5]
c=0
fr i in range(2,6,2):
if p[i-2]+p[i-1]==p[i]:
c+=1
print(c)
执行该段程序后,计算机显示的是( )
A. 1B. 2C. 3D. 4
【答案】A
【解析】
【详解】本题主要考查Pythn程序的执行。range(start, stp, [step]),start: 计数从 start 开始。默认是从 0 开始。例如range(5)等价于range(0, 5);stp: 计数到 stp 结束,但不包括 stp。例如:range(0, 5) 是[0, 1, 2, 3, 4]没有5;step:步长,默认为1。例如:range(0, 5) 等价于 range(0, 5, 1)。变量i依次取2、4,只有当i=2时,满足if判断条件,c=c+1=1,故本题选A选项。
11. 某Pythn程序实现的功能是;运行程序输入一个四位整数,能够判断该四位整数是否存在数字重复的位。程序代码如下:
n = int(input(“请输入一个四位正整数:”))
f = [0] * 10
while n > 0:
y = n % 10
①
n=n // 10
if ② :
print(“没有重复的位。”)
else:
print(“有重复的位。”)
划线处的代码应填( )
A. ① f[y] = 1 ② sum(f) < 4 #sum()将列表中所有元素求和
B. ① f[y] += 1 ② sum(f) < 4
C. ① f[y] = 1 ② sum(f) == 4
D. ① f[y] += 1 ② sum(f) == 4
【答案】C
【解析】
【详解】本题主要考查Pythn程序的综合应用。用f[y]标记四位整数上y,该数不论出现几次,都赋值为1,即第一空填 f[y] = 1,如果sum(f)==4,说明没有重复的位,反之有重复的位,即第二空填sum(f) == 4,故本题选C选项。
12. 运行如下程序代码,如果输入6,那么输出为( )
def f(a,b):
result=a*b
s=a+b
return result
a=int(input(“a=”))
b=15
s=f(a,b)
print(s)
A. 程序报错B. sC. 21D. 90
【答案】D
【解析】
【详解】本题考查的是自定义函数。如果输入6,b=15, result=a*b=6*15=90,s=f(a,b),返回值是90,故输出为90,选项D正确。
二、非选择题(本大题共3小题,其中第13小题9分,第14小题8分,第15小题9分,共26分)
13. 小李统计了浙江省1980年至2021年每年第一产业、第二产业、第三产业总值情况(单位:亿元),数据保存在“nianjian.xlsx”中,如图a所示。
图a图b
计算每年的生产总值合计,计算方法为:合计=第一产业+第二产业+第三产业。并绘制反映第三产业的线形图,如图b。
(1)请在划线①②处填入合适的代码。
imprt pandas as pd
imprt matpltlib.pyplt as plt
plt.rcParams[‘fnt.sans-serif’]=[‘KaiT’,‘SimHei’]
df=pd.read_excel (___)
_▲___________
x=df["年份"]
y= ___
plt.plt(x,y)
plt.shw()
(2)请为▲______处选择合适的代码(多选,填字母)。
A.=B2+C2+D2
B.合计=第一产业+第二产业+第三产业
C.df.合计=df.第一产业+df.第二产业+df.第三产业
D.df["合计"]=df["第一产业"]+df["第二产业"]+df["第三产业"]
(3)由图b可知,1980年至2021年第三产业的变化趋势为连续______(选填:增长/下降)。
(4)计算每年(1981~2021)的增长率,并统计出增长率最高的年份。
注:1981年增长率=(1981年合计—1980年合计)/1980年合计
n=len(df)
fr i in range(1,n):
minus= ___
df.at[i,“增长率”]=rund(minus/df.at[i-1,"合计"],4)
if i==1:
imax=1
elif df.at[i,"增长率"]>df.at[imax,"增长率"]:
___
print(df.at[imax,"年份"])
【答案】 ①. "nianjian.xlsx" ②. df["第三产业"] ③. CD ④. 增长 ⑤. df.at[i,"合计"]-df.at[i-1,"合计"] ⑥. imax=i
【解析】
【详解】本题主要考查Pythn程序的综合应用。①数据保存在“nianjian.xlsx”中,此处通过read_excel函数读取该表格,故填"nianjian.xlsx"。②绘制反映第三产业的线形图,因此纵坐标是第三产业数据,故填df[“第三产业”]。③合计=第一产业+第二产业+第三产业,因此可以是df.合计=df.第一产业+df.第二产业+df.第三产业 或 df[“合计”]=df[“第一产业”]+df[“第二产业"]+df[“第三产业”],故本题选CD选项。④由图b可知,1980年至2021年第三产业的变化趋势为连续增长。⑤1981年增长率=(1981年合计—1980年合计)/1980年合计,由代码 df.at[i,“增长率”]=rund(minus/df.at[i-1,“合计”],4),可知此处填df.at[i,“合计”]-df.at[i-1,“合计”]。⑥由if分支结构代码,可知当df.at[i,“增长率”]>df.at[imax,“增长率”]时,更新imax=i。
14. 孪生质数就是指相差2的素数对,例如3和5,5和7,11和13…。以下程序的功能为求出100以内的孪生质数。
imprt math
def judgss(n):#证明n是否为素数
i=2
while i<=int(math.sqrt(n)):
if n % i==0:
return False
i+=1
return ①____
ssd=[]
k=2
while k<100:
if judgss(k)==True and②___:
ssd.append(__▲____)# append()为列表添加元素
k+=2
else:③___
print(“100以内的孪生素数对有”,len(ssd),“对。分别为:”)
fr i in range(len(ssd)):
print(ssd[i])
(1)数据对:21和23______(选填:是/不是)孪生质数。
(2)完善①②③划线处的代码。
(3)程序段中▲处,填入的代码是______(单选,填字母)。
A.k,k+2 B.[k,k+2] C.[k],[k+2]
【答案】 ①. True ②. judgss(k+2)==True ③. k=k+1 或 k+=1 ④. 不是
⑤. B
【解析】
【详解】本题考查的是Pythn综合应用。(1)21不是质数,故21和23不是孪生质数。(2)若不能被其它数整除,则返回为真,故第一空应为:True;孪生质数就是指相差2的素数对,故第二空应为:judgss(k+2)==True;采用枚举方法找孪生质数,若没找到,则继续枚举下一个数,故第三空应为:k+=1或k=k+1。(3)由输出图例,可知,应以列表形式加入列表,故程序段中▲处,填入的代码是[k,k+2] ,选项B正确。
15. 小张有一架游标刻度不清的物理天平,和若干不同质量的砝码,个数与克数分别为:1个1g、2个2g、1个5g、1个10g、2个20g、2个50g。小张想通过编程知道能否使用这些砝码称出连续的不同质量,如能则输出有多少种不同质量与其质量的范围。
小张编程的想法为:将每个砝码看作不同的,即使质量一样也看成不同。小张所拥有的砝码数可以看作9个,对于每个砝码有可能被使用或不使用,因此砝码质量组合最多29种。小张从质量小的砝码开始尝试:先拿一个1g的砝码放入,这时出现第1种质量,将其记录。然后拿走1g砝码,将第1个2g砝码放入,这时出现第2种质量……。如果当前砝码组合的质量是前面产生质量+1,则记录当前组合质量;如果当前砝码组合的质量没有产生过且当前组合质量超过前面产生质量+1,则终止当前程序。具体砝码组合见下表所示:
(1)对于上表中各砝码的选择状态为111000000,则下一种选择状态为:______。
(2)具体代码如下,运行结果如下图示,在划线处填入合适代码。
def selct(f,n):#找出一种砝码的组合
i=0
while①___ and f[i]==1:
f[i]=0
i+=1
f[i]=1#选中第i种砝码
return f
weight=[12,2,5,10,20,20,50,50]#砝码
unweight=[]#记录砝码组合质量
n=len(weight)#砝码种数
f=[0]*n #记录砝码是否被取
fr i in range(2**n-1):
f=②___;
w=0
fr j in range(n):#依据选择状态,计算砝码质量
w+=③___
#将不同质量组合存入unweight列表
if len(unweight)==0:
unweight.append(w)#append()为列表添加元素
elif w nt in unweight and w==unweight[-1]+1:
unweight.append(w)
elif w nt in unweight:
break
print(“最多能称出”,len(unweight),“不同质量”)
print(“质量范围:”,unweight[0],“____”,④___)
【答案】 ①. 100100000 ②. i
【解析】
【详解】本题主要考查Pythn程序的综合应用。①对于上表中各砝码的选择状态为111000000,即产生质量位5g,则下一种选择状态为100100000,产生质量是6g。②先拿一个1g的砝码放入,这时出现第1种质量,将其记录。然后拿走1g砝码,将第1个2g砝码放入,这时出现第2种质量……。一共n个砝码数,循环变量i的初值为0,故此处循环条件是i
[3,5]
[5,7]
[11,13]
[17,19]
[29,31]
[41,43]
[59,61]
[71,73]
浙江省绍兴市2023-2024学年高一上学期1月期末技术-高中信息技术试卷(Word版附解析): 这是一份浙江省绍兴市2023-2024学年高一上学期1月期末技术-高中信息技术试卷(Word版附解析),文件包含浙江省绍兴市2023-2024学年高一上学期1月期末技术试题-高中信息技术Word版含解析docx、浙江省绍兴市2023-2024学年高一上学期1月期末技术试题-高中信息技术Word版无答案docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。
浙江省台州市2022-2023学年高一技术下学期期末试题(Word版附解析): 这是一份浙江省台州市2022-2023学年高一技术下学期期末试题(Word版附解析),共5页。试卷主要包含了0C. “98”D. “请输入等内容,欢迎下载使用。
浙江省绍兴市2022-2023学年高二技术下学期期末调测试题(Word版附解析): 这是一份浙江省绍兴市2022-2023学年高二技术下学期期末调测试题(Word版附解析),共12页。试卷主要包含了考试时间90分钟,满分100分,mp3"],["001等内容,欢迎下载使用。












