新教材数学苏教版必修第一册第7章 7.2 7.2.1　任意角的三角函数 课件

这是一份新教材数学苏教版必修第一册第7章 7.2 7.2.1　任意角的三角函数，文件包含第7章72721任意角的三角函数ppt、第7章72721任意角的三角函数doc等2份课件配套教学资源，其中PPT共55页， 欢迎下载使用。
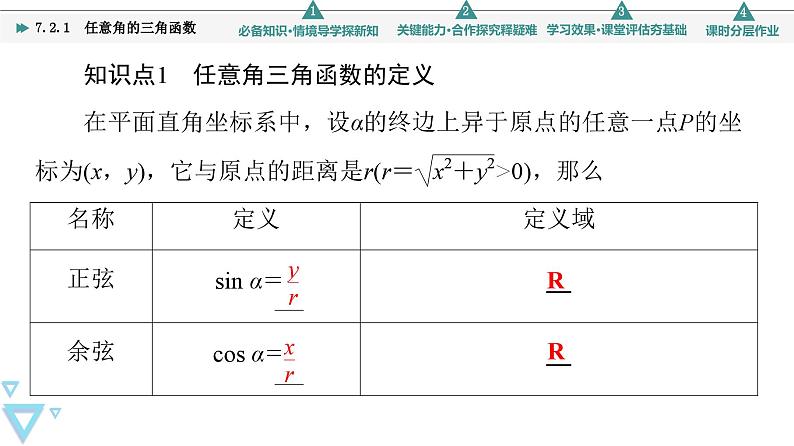
7.2　三角函数概念7.2.1　任意角的三角函数1．理解三角函数的定义，会使用定义求三角函数值．(重点、易错点)2．会判断给定角的三角函数值的符号．(重点)3．会利用三角函数线比较两个同名三角函数值的大小．(难点)1．通过三角函数的概念，培养数学抽象素养．2．借助公式的运算，提升数学运算素养．在初中我们学习了锐角三角函数，那么锐角三角函数是如何定义的？若将锐角放入直角坐标系中，你能用角的终边上的点的坐标来表示锐角三角函数吗？若以单位圆的圆心O为原点，你能用角的终边与单位圆的交点来表示锐角三角函数吗？那么，角的概念推广之后，三角函数的概念又该怎样定义呢？知识点1　任意角三角函数的定义在平面直角坐标系中，设α的终边上异于原点的任意一点P的坐标为(x，y)，它与原点的距离是r(r＝>0)，那么名称定义定义域正弦sin α＝R余弦cos α＝R正切tan α＝sin α，cos α，tan α分别称为正弦函数、余弦函数、正切函数，统称为三角函数．1．对于确定的角α，sin α，cos α，tan α的值是否随P点在终边上的位置的改变而改变？[提示]　不会．因为三角函数值是比值，其大小与点P(x，y)在终边上的位置无关，只与角α的终边位置有关，即三角函数值的大小只与角有关．2．若P(x，y)为角α与单位圆的交点，sin α，cos α，tan α的值怎样表示？[提示]　sin α＝y，cos α＝x，tan α＝．1．若角α的终边经过点P，则sin α＝________；cos α＝________；tan α＝________．－　　－1　[由题意可知OP＝＝1，∴sin α＝＝－；cos α＝＝；tan α＝＝－1．]知识点2　三角函数在各象限的符号2．(1)若α在第三象限，则sin αcos α________0；(填“＞”或“＜”)(2)cos 3tan 4________0．(填“>”或“<”)(1)＞　(2)＜　[(1)∵α在第三象限，∴sin α＜0，cos α＜0，∴sin αcos α＞0．(2)∵<3<π，π<4<，∴3是第二象限角，4是第三象限角．∴cos 3<0，tan 4>0，∴cos 3tan 4<0．]知识点3　三角函数线(1)有向线段：规定了方向(即规定了起点和终点)的线段；有向直线：规定了正方向的直线；有向线段的数量：若有向线段AB在有向直线l上或与有向直线l平行，根据有向线段AB与有向直线l的方向相同或相反，分别把它的长度添上正号或负号，这样所得的数，叫作有向线段的数量，记为AB．(2)三角函数线3．思考辨析(正确的打“√”，错误的打“×”)(1)α一定时，单位圆的正弦线一定． (　　)(2)在单位圆中，有相同正弦线的角必相等． (　　)[答案]　(1)√　(2)× 类型1　三角函数的定义及应用【例1】　(1)在平面直角坐标系中，角α的终边在直线y＝－2x上，求sin α，cos α，tan α的值；(2)当α＝－时，求sin α，cos α，tan α的值．[解]　(1)当α的终边在第二象限时，在α终边上取一点P(－1，2)，则r＝＝，所以sin α＝＝，cos α＝＝－，tan α＝＝－2．当α的终边在第四象限时，在α终边上取一点P′(1，－2)，则r＝＝，所以sin α＝＝－，cos α＝＝，tan α＝＝－2．(2) 当α＝－时，设α的终边与单位圆的交点坐标为P(x，y)(x>0，y<0)，根据直角三角形中锐角的邻边是斜边的一半，得x＝，由勾股定理得＋y2＝1，y<0，解得y＝－，所以P．因此sin α＝＝－，cos α＝＝，tan α＝＝－．[母题探究]1．将本例(1)的条件“y＝－2x”改为“x＋y＝0”，其他条件不变，结果又如何？[解]　直线x＋y＝0，即y＝－x，当α的终边在第二象限时，在α的终边上取一点P(－1，)，则r＝2，所以sin α＝，cos α＝－，tan α＝－；当α的终边在第四象限时，在α终边上取一点P′(1，－)，则r＝2，所以sin α＝－，cos α＝，tan α＝－．2．将本例(1)的条件“在直线y＝－2x上”，改为“过点P(－3a,4a)(a≠0)”，求2sin α＋cos α．[解]　因为r＝＝5|a|，①若a>0，则r＝5a，角α在第二象限，sin α＝＝＝，cos α＝＝＝－，所以2sin α＋cos α＝－＝1．②若a<0，则r＝－5a，角α在第四象限，sin α＝＝－，cos α＝＝，所以2sin α＋cos α＝－＋＝－1．1．已知角α终边上任意一点的坐标求三角函数值的方法(1)先利用直线与单位圆相交，求出交点坐标，然后再利用正、余弦函数的定义求出相应的三角函数值．(2)在α的终边上任选一点P(x，y)，设P到原点的距离为r(r>0)，则sin α＝，cos α＝．当已知α的终边上一点求α的三角函数值时，用该方法更方便．2．已知特殊角α，求三角函数值的方法(1)先设出角α的终边与单位圆交点坐标，由锐角三角形的定义结合勾股定理求出该点的坐标．(2)利用三角函数的定义，求出α的三角函数值(此时P到原点的距离r＝1)．3．当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．1．已知角θ终边上一点P(x,3)(x≠0)，且cos θ＝x，求sin θ，tan θ．[解]　由题意知r＝，由三角函数定义得cos θ＝＝．又∵cos θ＝x，∴＝x．∵x≠0，∴x＝±1．当x＝1时，P(1,3)，此时sin θ＝＝，tan θ＝＝3．当x＝－1时，P(－1,3)，此时sin θ＝＝，tan θ＝＝－3．2． 当α＝时，求sin α，cos α，tan α的值．[解]　当α＝时，设α的终边与单位圆的交点坐标为P(x，y)(x<0，y<0)，根据直角三角形中锐角的邻边是斜边的一半，得x＝－，由勾股定理得＋y2＝1，y<0，解得y＝－， 所以P．因此sin α＝＝－，cos α＝＝－，tan α＝＝． 类型2　三角函数值的符号【例2】　(1)若角θ同时满足sin θ<0且tan θ<0，则角θ的终边一定位于(　　)A．第一象限　　　　　　 B．第二象限C．第三象限     D．第四象限(2)判断下列各式的符号．①sin 2 015° cos 2 016° tan 2 017°；②tan 191°－cos 191°；③sin 2 cos 3 tan 4．(1)D　[由sin θ<0，可知θ的终边可能位于第三或第四象限，也可能与y轴的负半轴重合．由tan θ<0，可知θ的终边可能位于第二象限或第四象限，故θ的终边只能位于第四象限．](2)[解]　①∵2 015°＝1 800°＋215°＝5×360°＋215°，2 016°＝5×360°＋216°，2 017°＝5×360°＋217°，∴它们都是第三象限角，∴sin 2 015°<0，cos 2 016°<0，tan 2 017°>0，∴sin 2 015° cos 2 016° tan 2 017°>0．②∵191°角是第三象限角，∴tan 191°>0，cos 191°<0，∴tan 191°－cos 191°>0．③∵<2<π，<3<π，π<4<，∴2是第二象限角，3是第二象限角，4是第三象限角，∴sin 2>0，cos 3<0，tan 4>0，∴sin 2 cos 3 tan 4<0．判断三角函数值在各象限符号的攻略1基础：准确确定三角函数值中各角所在象限.2关键：准确记忆三角函数在各象限的符号.3注意：用弧度制给出的角常常不写单位，不要误认为角度制导致象限判断错误.3．判断下列式子的符号：(1)tan 108°·cos 305°；(2)；(3)tan 120°·sin 269°．[解]　(1)∵108°是第二象限角，∴tan 108°＜0．∵305°是第四象限角，∴cos 305°＞0．从而tan 108°·cos 305°＜0．(2)∵是第二象限角，是第四象限角，是第二象限角，∴cos ＜0，tan＜0，sin ＞0．从而＞0．(3)∵120°是第二象限角，∴tan 120°＜0，∵269°是第三象限角，∴sin 269°＜0．从而tan 120°·sin 269°＞0． 类型3　应用三角函数线解三角不等式【例3】　在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合：(1)sin α≥；(2)cos α≤－．[解]　(1)作直线y＝交单位圆于A，B两点，连接OA，OB，则OA与OB围成的区域(图①阴影部分)即为角α的终边的范围，故满足条件的角α的集合为．(2)作直线x＝－交单位圆于C，D两点，连接OC，OD，则OC与OD围成的区域(图②阴影部分)即为角α终边的范围，故满足条件的角α的集合为．利用三角函数线解三角不等式的方法1正弦、余弦型不等式的解法,对于sin x≥b，cos x≥asin x≤b，cos x≤a，求解的关键是恰当地寻求点，只需作直线y＝b或x＝a与单位圆相交，连接原点与交点即得角的终边所在的位置，此时再根据方向即可确定相应的范围.2正切型不等式的解法,对于tan x≥c，取点1，c，连接该点和原点并反向延长，即得角的终边所在的位置，结合图象可确定相应的范围.4．求函数f(x)＝＋ln的定义域．[解]　由题意，自变量x应满足不等式组即则不等式组的解的集合如图(阴影部分)所示，∴函数f(x)的定义域为．1．若sin α＜0，tan α＞0，则α终边所在象限是(　　)A．第一象限　　　　　　 B．第二象限C．第三象限     D．第四象限C　[由sin α＜0可知α的终边落在第三、四象限及y轴的负半轴上，由tan α＞0可知α的终边落在第一、三象限内，故同时满足sin α＜0，tan α＞0的角α为第三象限角．]2．(多选题)下列三角函数判断错误的是(　　)A．sin 165°>0     B．cos 280°<0C．tan 170°>0     D．tan 310°>0BCD　[∵90°<165°<180°，∴sin 165°>0．又270°<280°<360°，∴cos 280°>0．又270°<310°<360°，∴tan 310°<0,90°<170°<180°，∴tan 170°<0．]3．已知角α终边过点P(1，－1)，则tan α的值等于________．－1　[由三角函数定义知tan α＝＝－1．]4．已知角α终边过P，则cos α等于________．　[由三角函数定义可知，角α的终边与单位圆交点的横坐标为角α的余弦值，故cos α＝．]5．已知sin θ·tan θ<0，那么θ是第________象限角．二或三　[因为sin θ·tan θ<0，所以sin θ<0，tan θ>0或sin θ>0，tan θ<0，若sin θ>0，tan θ<0，所以θ在第二象限．若sin θ<0，tan θ>0，则θ在第三象限．]回顾本节知识，自我完成以下问题．1．三角函数值的大小与取点有关吗？与什么有关？[提示]　三角函数值的大小与终边所在的位置有关，与取点无关．2．求一个角的三角函数值需确定几个量？分别是什么？[提示]　确定三个量，角的终边上异于原点的点的横、纵坐标及其到原点的距离．3．已知角的大小，怎样利用定义求三角函数值？[提示]　确定出角的终边与单位圆的交点坐标．