广东省广州市黄埔区火电学校2022—2023学年下学期七年级期中数学试卷

这是一份广东省广州市黄埔区火电学校2022—2023学年下学期七年级期中数学试卷，共14页。
1．（3分）在下列实数中，是无理数的是（ ）
A．B．C．1.01001D．
2．（3分）下列图形中，能通过某个基本图形经过平移得到的是（ ）
A．B．
C．D．
3．（3分）在平面直角坐标系中，属于第二象限的点是（ ）
A．（2，3）B．（2，﹣3）C．（﹣2，3）D．（﹣2，﹣3）
4．（3分）如图，将△ABC向右平移得到△DEF，已知A，D两点的距离为1，CE＝2，则BF的长为（ ）
A．5B．4C．3D．2
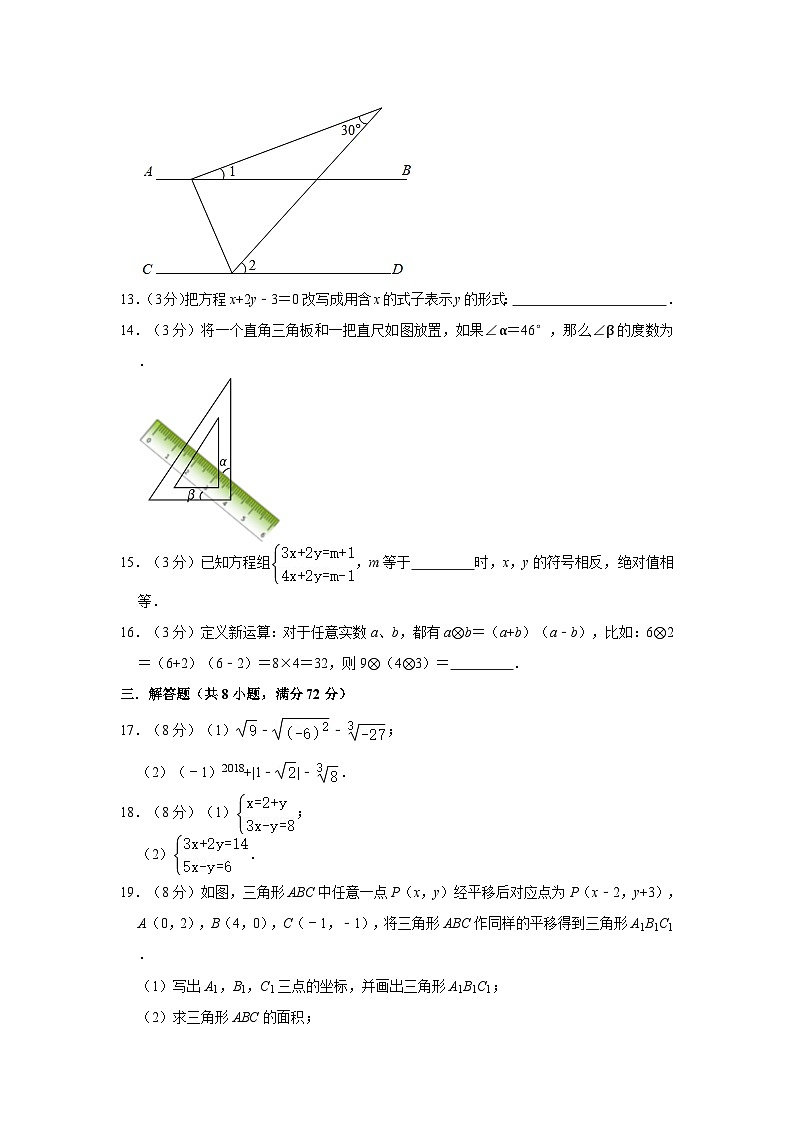
5．（3分）若点P（a，b）在第四象限，则点M（﹣a，﹣b）在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
6．（3分）下列几组解中，二元一次方程2x+3y＝0的解是（ ）
A．B．C．D．
7．（3分）在平面直角坐标系中，点P（m，n）满足，则点P的坐标是（ ）
A．（3，4）B．（4，3）C．（﹣3，4）D．（4，﹣3）
8．（3分）若将三个数，，表示在数轴上，其中能被如图所示的墨迹覆盖的数是（ ）
A．
B．
C．
D．不是A、B、C中的任意一数
9．（3分）丫丫从学校骑自行车出发到图书馆，中途因道路施工步行了一段路，一共用了1.5小时到达图书馆．她骑车的平均速度是15km/h，步行的平均速度是5km/h，路程全长20km，设丫丫骑车的时间是x小时，步行的时间是y小时．则可列方程为（ ）
A．B．
C．D．
10．（3分）如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向不断地移动，每移动一个单位，得到点A1（0，1）、A2（1，1）、A3（1，0）、A4（2，0）…，那么点A2022的坐标为（ ）
A．（1011，0）B．（1011，1）C．（2022，0）D．（2022，1）
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）比较大小： 6， ．（用“＞”或“＜”连接）
12．（3分）将含30°角的三角板如图摆放，AB∥CD，若∠1＝20°，则∠2的度数是 ．
13．（3分）把方程x+2y﹣3＝0改写成用含x的式子表示y的形式： ．
14．（3分）将一个直角三角板和一把直尺如图放置，如果∠α＝46°，那么∠β的度数为 ．
15．（3分）已知方程组，m等于 时，x，y的符号相反，绝对值相等．
16．（3分）定义新运算：对于任意实数a、b，都有a⊗b＝（a+b）（a﹣b），比如：6⊗2＝（6+2）（6﹣2）＝8×4＝32，则9⊗（4⊗3）＝ ．
三．解答题（共8小题，满分72分）
17．（8分）（1）﹣﹣；
（2）（﹣1）2018+|1﹣|﹣．
18．（8分）（1）；
（2）．
19．（8分）如图，三角形ABC中任意一点P（x，y）经平移后对应点为P（x﹣2，y+3），A（0，2），B（4，0），C（﹣1，﹣1），将三角形ABC作同样的平移得到三角形A1B1C1．
（1）写出A1，B1，C1三点的坐标，并画出三角形A1B1C1；
（2）求三角形ABC的面积；
（3）已知点P在y轴上，且三角形PAB的面积等于三角形ABC的面积，求P点坐标．
20．（8分）一个正数x的两个不同的平方根分别是2a﹣1和﹣a+2．
（1）求a和x的值；
（2）求4x+9a的平方根和立方根．
21．（8分）如图，已知∠1＝∠2，∠3＝∠4，∠5＝∠A，试说明：BE∥CF．
完善下面的解答过程，并填写理由或数学式：解：
∵∠3＝∠4（已知）
∴AE∥ （ ）
∴∠EDC＝∠5（ ）
∵∠5＝∠A（已知）
∴∠EDC＝ （等量代换）
∴DC∥AB（ ）
∴∠5+∠ABC＝180°（ ）
即∠5+∠2+∠3＝180°
∵∠1＝∠2（已知）
∴∠5+∠1+∠3＝180°（ ）
即∠BCF+∠3＝180°
∴BE∥CF（ ）．
22．（10分）已知点P（2a﹣2，a+5），解答下列各题．
（1）点P在x轴上，求出点P的坐标．
（2）点Q的坐标为（4，5），直线PQ∥x轴，求出点P的坐标．
（3）若点P在第二象限，且它到x轴、y轴的距离相等，求a2020+2020的值．
23．（10分）现有一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车，为节约成本，每辆货车均装满．已知过去两次租用这两种货车的运货情况如下表所示：
（1）求甲、乙两种货车每辆可装多少吨货物？
（2）现租用该公司3辆甲种货车及4辆乙种货车一次刚好运完这批货，如果按每吨付运费30元计算，问货主应付运费多少元？
24．（12分）如图，已知点B（a，b），且a，b满足|2a+b﹣13|+＝0．过点B分别作BA⊥x轴、BC⊥y轴，垂足分别是点A、C．
（1）求出点B的坐标；
（2）点M是边OA上的一个动点（不与点A重合），∠CMA的角平分线交射线CB于点N，在点M运动过程中，的值是否变化？若不变，求出其值；若变化，说明理由；
（3）在四边形OABC的边上是否存在点P，使得BP将四边形OABC分成面积比为1：4的两部分？若存在，请直接写出点P的坐标；若不存在，说明理由．
参考答案与试题解析
一．选择题（共10小题，满分30分，每小题3分）
1． 解：是分数，1.01001是有限小数，＝2是整数，这些都属于有理数；
是无理数．
故选：A．
2． 解：根据平移变换的性质可知选项D满足条件，
故选：D．
3． 解：∵点在第二象限，
∴点的横坐标是负数，纵坐标是正数，
∴只有C符合要求．
故选：C．
4． 解：∵将△ABC向右平移得到△DEF，
∴AD＝BE＝CF＝1，
∵EC＝2，
∴BF＝BE+EF+CF＝1+2+1＝4，
故选：B．
5． 解：∵点P（a，b）在第四象限，
∴a＞0，b＜0，
∴﹣a＜0，﹣b＞0，
∴点M（﹣a，﹣b）在第二象限．
故选：B．
6． 解：A、把代入方程得：左边≠右边，故不是方程的解，不符合题意；
B、把代入方程得：左边＝右边，故是方程的解，符合题意；
C、把代入方程得：左边≠右边，故不是方程的解，不符合题意；
D、把代入方程得：左边≠右边，故不是方程的解，不符合题意；
故选：B．
7． 解：∵，
∴m+3＝0，4﹣n＝0，
∴m＝﹣3，n＝4，
∴P（﹣3，4），
故选：C．
8． 解：∵﹣2＜﹣＜﹣1，2＜＜3，3＜＜4，且墨迹覆盖的范围是3与4之间，
∴能被墨迹覆盖的数是3与4之间．．
故选：C．
9． 、解：设丫丫骑车的时间是x小时，步行的时间是y小时，
由题意可得：，
故选：B．
10． 解：∵点A1（0，1）、A2（1，1）、A3（1，0）、A4（2，0）、A5（2，1）、A6（3，1）、A7（3，0）、A8（4，0）、A9（4，1）、…，
∴点A4n+2（n为自然数）的坐标为（2n+1，1），
∴点A2022的坐标为（1011，1）．
故选：B．
二．填空题（共6小题，满分18分，每小题3分）
11． 解：∵＞，
∴＞6；
∵＞＝2，
∴﹣1＞1，
∴．
故答案为：＞，＞．
12． 解：如图：
∵∠1＝20°，∠3＝∠1+30°，
∴∠3＝∠1+30°＝20°+30°＝50°，
∵AB∥CD，
∴∠2＝∠3＝50°．
故答案为：50°．
13． 解：方程x+2y﹣3＝0，
解得：y＝．
故答案为：y＝
14． 解：如图，根据题意得：∠ACB＝90°，DE∥FG，
过点C作CH∥DE交AB于H，
∴CH∥DE∥FG，
∴∠BCH＝∠α＝46°，
∴∠HCA＝90°﹣∠BCH＝44°，
∴∠β＝∠HCA＝44°．
故答案为：44°．
15． 解：，
②﹣①，得x＝﹣2，
把x＝﹣2代入①，得﹣6+2y＝m+1，
解得y＝0.5m+3.5，
当x，y的符号相反，绝对值相等，可得0.5m+3.5＝2，
解得：m＝﹣3．
故答案为：﹣3．
16． 解：由新定义得：
9⊗（4⊗3）
＝9⊗[（4+3）（4﹣3）]
＝9⊗7
＝（9+7）（9﹣7）
＝32，
故答案为：32．
三．解答题（共8小题，满分72分）
17． 解：（1）﹣﹣
＝3﹣6﹣（﹣3）
＝3﹣6+3
＝0；
（2）（﹣1）2018+|1﹣|﹣
＝1+﹣1﹣2
＝﹣2．
18． 解：（1），
①代入②，可得：3（2+y）﹣y＝8，
解得y＝1，
把y＝1代入①，可得：x＝2+1＝3，
∴原方程组的解是．
（2），
①+②×2，可得13x＝26，
解得x＝2，
把x＝2代入①，解得y＝4，
∴原方程组的解是．
19． 解：（1）由题意得，△ABC是向左平移2个单位，向上平移3个单位得到的△A1B1C1，
∵A（0，2），B（4，0），C（﹣1，﹣1），
∴A1（﹣2，5），B1（2，3），C1（﹣3，2）．
如图，△A1B1C1即为所求．
（2）△ABC的面积为5×3﹣﹣﹣＝7．
（3）设点P的坐标为（0，y），
∴△PAB的面积为＝2|y﹣2|，
∵△PAB的面积等于△ABC的面积，
∴2|y﹣2|＝7，
解得y＝或﹣．
∴点P的坐标为（0，）或（0，﹣）．
20． 解：（1）∵一个正数的两个不同的平方根互为相反数，
∴2a﹣1+（﹣a+2）＝0，
解得：a＝﹣1，
∴x＝（2a﹣1）2＝（﹣3）2＝9；
（2）∵4x+9a＝4×9+9×（﹣1）＝27，
∴，
27的立方根为3．
21． 解：∵∠3＝∠4（已知），
∴AE∥BC（内错角相等，两直线平行），
∴∠EDC＝∠5（两直线平行，内错角相等），
∵∠5＝∠A（已知），
∴∠EDC＝∠A（等量代换），
∴DC∥AB（同位角相等，两直线平行），
∴∠5+∠ABC＝180°（两直线平行，同旁内角互补），
即∠5+∠2+∠3＝180°，
∵∠1＝∠2（已知），
∴∠5+∠1+∠3＝180°（等量代换），
即∠BCF+∠3＝180°，
∴BE∥CF（同旁内角互补，两直线平行）．
故答案为：BC；内错角相等，两直线平行；两直线平行，内错角相等；∠A；同位角相等，两直线平行；两直线平行，同旁内角互补；等量代换；同旁内角互补，两直线平行．
22． 解：（1）∵点P在x轴上，
∴a+5＝0，
∴a＝﹣5，
∴2a﹣2＝2×（﹣5）﹣2＝﹣12，
∴点P的坐标为（﹣12，0）．
（2）点Q的坐标为（4，5），直线PQ∥x轴，
∴a+5＝5，
∴a＝0，
∴2a﹣2＝﹣2，
∴点P的坐标为（﹣2，5）．
（3）∵点P在第二象限，且它到x轴、y轴的距离相等，
∴2a﹣2＝﹣（a+5），
∴2a﹣2+a+5＝0，
∴a＝﹣1，
∴a2020+2020＝（﹣1）2020+2020＝2021．
∴a2020+2020的值为2021．
23． 解：（1）设甲种货车每辆可装x吨货物，乙种货车每辆可装y吨货物，
依题意得：，
解得：．
答：甲种货车每辆可装4吨货物，乙种货车每辆可装3吨货物．
（2）30×（4×3+4×3）
＝30×（12+12）
＝30×24
＝720（元）．
答：货主应付运费720元．
24． 解：（1）∵|2a+b﹣13|+＝0．
∴，
∴，
∴B（5，3）；
（2）的值不变，其值为1，
理由：∵BC⊥y轴，
∴BC∥x轴，
∴∠CNM＝∠AMN，
∵MN是∠CMA的平分线，
∴∠CMN＝∠AMN，
∴∠CNM＝∠CMN，
∴＝1；
（3）由（1）知，B（5，3），
∵BA⊥x轴、BC⊥y，
∴A（5，0），C（0，3），
∵BA⊥x轴、BC⊥y，
∴∠OCB＝∠OAB＝90°＝∠AOC，
∴四边形AOBC是矩形，
∴AB＝OC＝3，BC＝OA＝5，
∴S四边形OABC＝OA•OC＝15，
当点P在OC上时，设P（0，m），
∴CP＝3﹣m，
∴S△BPC＝BC•CP＝×5（3﹣m）＝（3﹣m），
∵BP将四边形OABC分成面积比为1：4的两部分，
∴S△BPC＝S四边形OABC＝3，
∴（3﹣m）＝3，
∴m＝，
∴P（0，）
当点P在OA上时，设P（0，n），
∴AP＝5﹣n，
∴S△BPC＝AB•AP＝×3（5﹣n）＝（5﹣n），
∵BP将四边形OABC分成面积比为1：4的两部分，
∴S△BPA＝S四边形OABC＝3，
∴（5﹣n）＝3，
∴n＝3，
∴P（3，0），
即：满足条件的点P的坐标为（0，）或（3，0）．
第一次
第二次
甲种货车辆数（单位：辆）
2
5
乙种货车辆数（单位：辆）
3
6
该次运货物吨数（单位：吨）
17
38