华师大版七年级数学上册第一单元《走进数学世界》教案

第1章 走进数学世界

第1课时 数学伴我们成长人类离不开数学

【基本目标】

1.使学生初步认识到数学与现实世界的密切联系，懂得数学的价值，形成用数学的意识；

2.使学生初步体验到数学是一个充满着观察、实验、归纳、类比和猜测的探索过程.

【教学重点】

加强数学意识.

【教学难点】

数学能力的培养.

一、情境导入，激发兴趣

1. 现在让我们进入时空的隧道，回忆我们的成长历程：

出生——学前——小学，我们每一天都在接触数学并不断学习它，相信吗？不妨大家从不同阶段来举出一些我们身边或亲身经历的例子，试一试.

2．进入小学，我们正式开始学习数学，回忆一下，在小学阶段我们学习的主要数学知识有哪些？

【教学说明】学生很容易能说出数学与生活的联系，感受数学与生活有着密切的联系，激发学生学习数学的兴趣.

二、合作探究，探索新知

1.数学伴我们成长

人来到世界上的第一天就遇到数学，数学将哺育着你的成长.数学知识开阔了你的视野，改变了你的思维方式，使你变得更聪明了.

从生活的一系列人生活动中，我们会逐渐意识到这一切的一切都和数、数的运算、数的比较、图形的大小、图形的形状、图形的位置有关.另外，数学知识开阔了你的视野，改变了你的思维方式，使我们变得更聪明.

【教学说明】使学生明确数学伴随我们成长，数学与我们的生活密切相关.

2.人类离不开数学

（1）自然界中的数学不胜枚举，如蜜蜂营造的蜂房,其表面由正六边形构成.

【教学说明】观察图形，引起学生探究的兴趣.

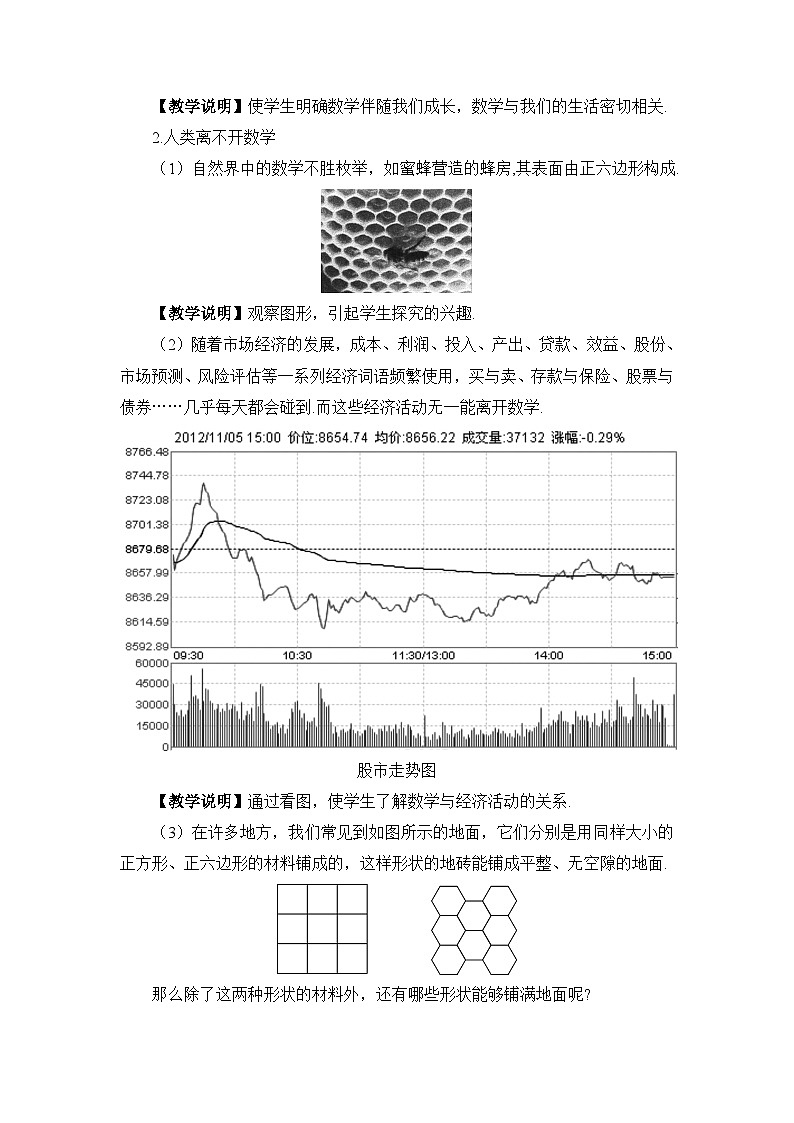
（2）随着市场经济的发展，成本、利润、投入、产出、贷款、效益、股份、市场预测、风险评估等一系列经济词语频繁使用，买与卖、存款与保险、股票与债券……几乎每天都会碰到.而这些经济活动无一能离开数学.

股市走势图

【教学说明】通过看图，使学生了解数学与经济活动的关系.

（3）在许多地方，我们常见到如图所示的地面，它们分别是用同样大小的正方形、正六边形的材料铺成的，这样形状的地砖能铺成平整、无空隙的地面.

那么除了这两种形状的材料外，还有哪些形状能够铺满地面呢?

我们还可以举出以下各种形状的图案，它们能够铺满地面.

【教学说明】让学生回想家里和广场上地砖的形状，互相讨论，画图说明.

（4）现在我们走进商场，看看购物中的数学.

某商场平时实行打折销售，现推出如下“有奖销售”活动：

请你计算奖金的总金额是多少，占10000张奖券的最低销售总额的百分比是多少.

奖品的总金额是：2000×2+800×10+200×20+100×50+50×200+20×1000=51000

它占10000张奖券对应的最低销售总额400×10000=4000000的1.257%.

【教学说明】学生通过计算，发现奖品总金额占10000张奖券的最低销售总额的比例很低，说明数学在生活中是有用的.

三、练习反馈，巩固提高

数学知识的学习，不仅开阔了我们的视野，而且改变了我们的思维方式，使我们变得更加聪明了.发挥一下我们的聪明才智，尝试解决下面的两个问题：

1. (1)计算并观察下列三组算式：

(2)已知25×25=625，则24×26=_______.

(3)你能举出一个类似的例子吗？

(4)更一般地，若a×a=m，则(a+1)(a-1)= _______.

2.今有一块正方形土地，要在其上修筑两条笔直的道路，使道路把这片土地分成形状相同且面积相等的4部分，若道路的宽度忽略不计，请你设计三种不同的修筑方案．（只需画简图）

【教学说明】学生通过练习，发展思维能力，培养一定的数学探究能力和合作意识.

【答案】1.（1）144 143（2）624（3）13×13=169,12×14=168（4）m-1

四、师生互动，课堂小结

1.数学伴我们成长，人类离不开数学.

2.通过本节课的学习，你有哪些收获？还有哪些困惑？请与老师或同学进行交流.

【教学说明】学生回顾本节课所学内容，进一步提升学生学习数学的兴趣.

完成本课时对应的练习.

新课标明确告诉我们，教学已不再是教师的专利了，应把学习的主动权还给学生.只有让学生在和谐的学习氛围中互相质疑、互相欣赏、互相帮助才能把学生吸引住.通过观察、思考、计算、论证等一系列活动，使学生明确数学与我们的生活紧密相连，增强学生学习数学的兴趣.

第2课时 人人都能学会数学

【基本目标】

1.使学生对数学产生一定的兴趣，获得学好数学的自信心；

2.使学生学会与他人合作，养成独立思考与合作交流的习惯；

3.使学生在数学活动中获得对数学良好的感性认识，初步体验到什么是“做数学”.

【教学重点】

如何培养学生对数学的兴趣.

【教学难点】

学生对数学的感性认识.

一、情境导入，激发兴趣

数学并不神秘，不是只有天才才能学好数学，只要通过努力，人人都能学好数学.阅读《华罗庚的故事》，谈谈你的感受.

【教学说明】用科学家的故事来激励学生去学好数学，认识数学，认识自我.

二、合作探究，探索新知

1.学好数学还要把数学应用于实际问题.下面让我们试着来解决一个实际问题.如图是6级台阶侧面的示意图，如果要在台阶上铺地毯，那么至少要买地毯多少米？

要在台阶上铺地毯，实际上并不需要测出台阶的长度.我们把上面的图想象为由一根绳子围成的图形，将它拉成为一个长和宽分别为2.8米和1米的长方形.因此，地毯的长就是2.8+1=3.8(米)，也就是要买地毯3.8米.

【教学说明】通过求地毯的长，培养学生的空间想象力，进一步强调数学在实际生活中的作用.

2.去掉一个最高分和一个最低分

在歌手电视大奖赛上，10个评委亮分之后，为什么要去掉一个最高分和一个最低分?

大奖赛上，常常要去掉一个最高分和一个最低分，其目的是要略去评委评分中可能出现的异常值，使得一个或两个评委的个人意愿不至于影响参赛歌手的总成绩.

让我们再看一个极端的例子.某大奖赛有7名评委，他们给甲乙两选手打的分数分别是：

甲：9.55,9.55,9.55,9.55,9.55,9.60,9.90

乙：9.50,9.60,9.60,9.60,9.60,9.60,9.70

凭直觉，你认为哪个选手比较好一点？

（1）请直接算出7个分数的平均数.

甲的平均分：(9.55+9.55+9.55+9.55+9.55+9.60+9.90)÷7=9.607

乙的平均分：（9.50+9.60+9.60+9.60+9.60+9.60+9.70）÷7=9.60

（2）去掉一个最高分和一个最低分，计算剩下5个数的平均数.

甲的平均分：(9.55+9.55+9.55+9.55+9.60)÷5=9.56

乙的平均分：（9.60+9.60+9.60+9.60+9.60）÷5=9.60

（3）通过计算，想一想哪种方式更合适？

 显然，用第二种方式比较符合直觉.由于评委给甲打分时出现极端的最高分（9.90），所以直接计算7个分数的平均数会出现偏差，而采用“去掉一个最高分和一个最低分”就可以避免这样的偏差，显得较为公平.

【教学说明】通过对比，使学生了解数学在生活中的重要作用，增强学生学习数学、研究数学的兴趣.

三、练习反馈,巩固提高

1.设定期储蓄1年期、2年期、3年期、5年期的年利率分别为2.25%，2.43%,2.70%和2.88%,试计算1000元本金分别参加这四种储蓄，到期所得的利息各为多少.（国家规定：个人储蓄从1999年11月1日起开始征收利息税，征收的税率为利息的20%）分析结果，你能发现什么？（提示：利息=本金×年利率×储存年数）

【答案】1年期利息18元，2年期利息38.88元，3年期利息64.8元，5年期利息115.2元．发现：参加定期储蓄，存期越长，得到利息越大．

2.在第十届“哈药六杯”全国青年歌手电视大奖赛，8位评委给某选手所评分数如下表，计分方法是：去掉一个最高分，去掉一个最低分，其余分数的平均分作为该选手的最后得分.请你算一算该选手的最后得分．

【答案】9.72

【教学说明】通过练习，让学生体会用数学.

四、师生互动，课堂小结

通过以上两节的学习，我们一定会喜欢上数学，并希望它天天陪伴你.在以后的学习中，我们将在小学的基础上学到更多新的知识.

完成本课时对应的练习.

在本节课的教学中，紧紧抓住数学与实际生活的联系，让学生尝试用数学知识去解决实际生活中的一些简单问题，增强学生学习数学的兴趣，初步培养学生应用数学的意识.

本章复习

【基本目标】

1.结合具体例子，体会数学与我们的成长密切相关，人类离不开数学；激发学生的学习兴趣，增强他们的数学应用意识.

2.尝试独立思考，体验数学问题的探索过程；初步获得成功体验，树立“人人都能学好数学”的自信心.

3.经历观察、操作、思考、交流等活动过程，初步体会什么是做数学、怎样做数学；激发对数学的好奇心和求知欲，并在数学活动中获得成功的体验.

【教学重点】

激发学生学习数学的兴趣，体验数学问题的探索过程.

【教学难点】

独立解决问题的能力.

一、知识框图，整体把握

二、典例精析，温故知新

例1 一个数减去4，再除以2，然后加上3 ，再乘以2，最后得8，问这个数是多少？

分析：可用算术法或代数法解，答案是6.

例2 这是一道数学填空题，是从美国哈佛大学入学试卷中选出的.请在下面这一组图形符号中找出它们所蕴含的内在规律，然后在横线处填上恰当的图.

分析：已知条件是数字1,2,3,4,5,7的镜像图.这个有趣的题目说明学习中需要细致观察，需要对数字、图形敏感，也需要想象.

例3 （可以使用多媒体课件）有人在甬江大桥下做赌博游戏，几个围观者跃跃欲试.主持人给大家看，公文包里有５个乒乓球，其中两个球上写有大红“福”字.他吆喝着人们去摸“福”，如果一下子同时摸中这两只就能获奖.旁边贴有“海报”，上面写着：S

分析：发现摸彩者获奖的可能性仅有10%，赢率微乎其微.接着老师当场拿出教具，请几位学生试验手气，果然均难以一下子摸到“双福”.所以在这场不公平的游戏中，摸彩者摸到的不是福气，而是晦气.赌博有害，我们不仅不要参与，而且要用数学的眼光，来揭穿它的骗人的本质.

例4 我国著名数学家苏步青教授年轻时候做过这样一道题：“甲和乙从东西两地同时出发，相对而行，两地相距10千米.甲每小时走3千米，乙每小时走2千米，几小时两人相遇？如果甲带了一只狗，和甲同时出发，狗以每小时5千米的速度向乙奔去，遇到乙后即回头向甲奔去；遇到甲又回头向乙奔去，直到甲乙两人相遇时狗才停住.问这只狗共奔跑了多少千米？”

分析：要从整体的角度看问题，狗奔跑的时间是两人相遇的时间.

解：10÷（3＋2）×5=10（千米）.

三、拓展训练，巩固提高

1.猜谜语：2、4、6、8、10（打一成语）_______________________.

2.一群整数朋友按照一定的规律排成一行，可排在  位置的数跑掉了，请帮它们把跑掉的朋友找回来:

（1）5，8，11，14，  ，20；

（2）1，3，7，15，31，63，  ；

（3）1，1，2，3，5，8，  ，21．

3.将1~8这八个整数分别填入下列括号内，使得等式成立：

【答案】1. 无独有偶

2.（1）17（2）127（3）13

3.

完成本课时对应的练习.

通过典型例题的探究，培养学生观察、思考、猜想、验证的数学思维过程，初步培养数学探究意识，提高学生数学思维能力.