专题09 巧用隐圆，妙解压轴-2022-2023学年九年级数学上学期期末分类复习满分冲刺（苏科版）

这是一份专题09 巧用隐圆，妙解压轴-2022-2023学年九年级数学上学期期末分类复习满分冲刺（苏科版），文件包含专题09巧用隐圆妙解压轴原卷版docx、专题09巧用隐圆妙解压轴解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

典例分析：
实例讲解:(包含以上多种模型)
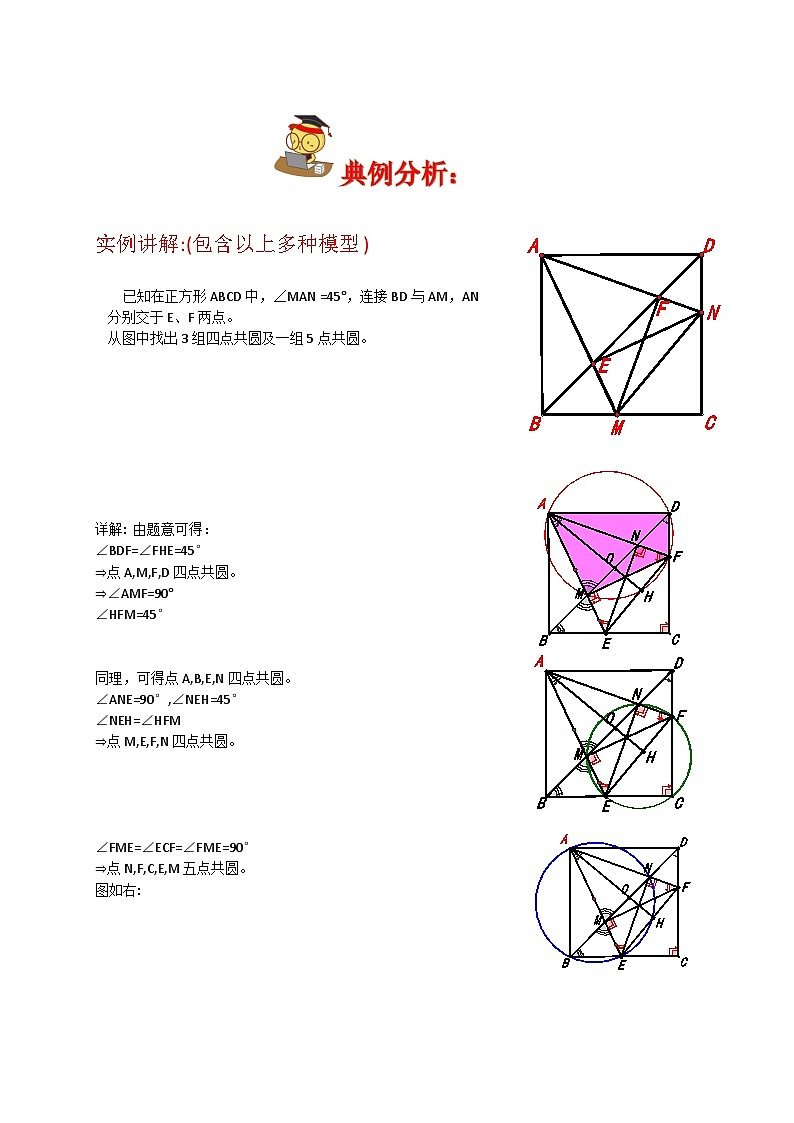
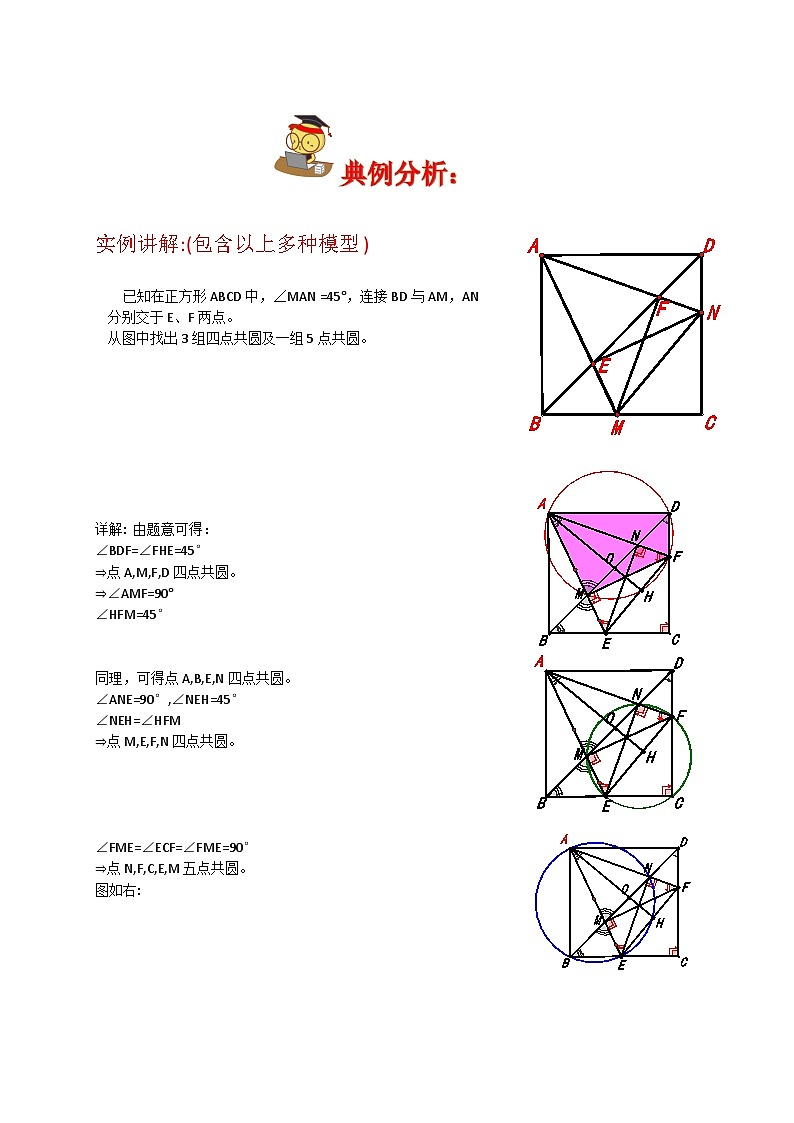
已知在正方形ABCD中，∠MAN =45°，连接BD与AM，AN
分别交于E、F两点。
从图中找出3组四点共圆及一组5点共圆。
详解: 由题意可得：
∠BDF=∠FHE=45°
⇒点A,M,F,D四点共圆。
⇒∠AMF=90°
∠HFM=45°
同理，可得点A,B,E,N四点共圆。
∠ANE=90°,∠NEH=45°
∠NEH=∠HFM
⇒点M,E,F,N四点共圆。
∠FME=∠ECF=∠FME=90°
⇒点N,F,C,E,M五点共圆。
图如右:
实战训练

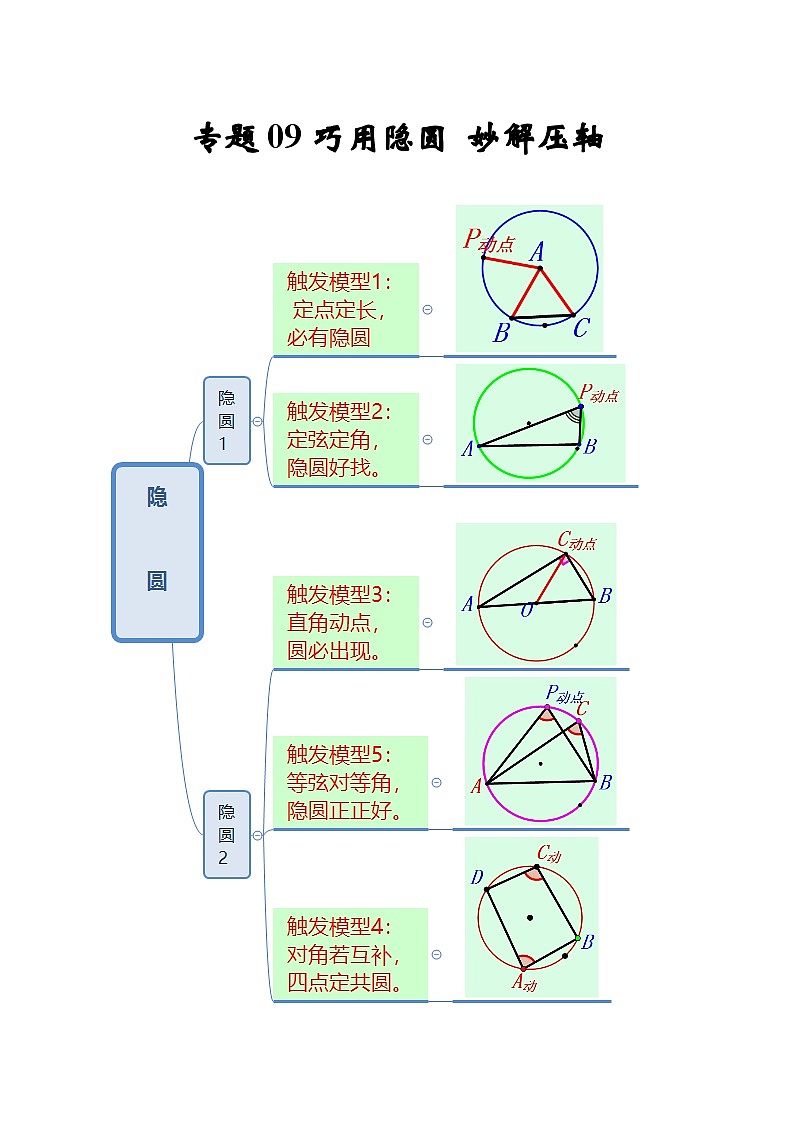
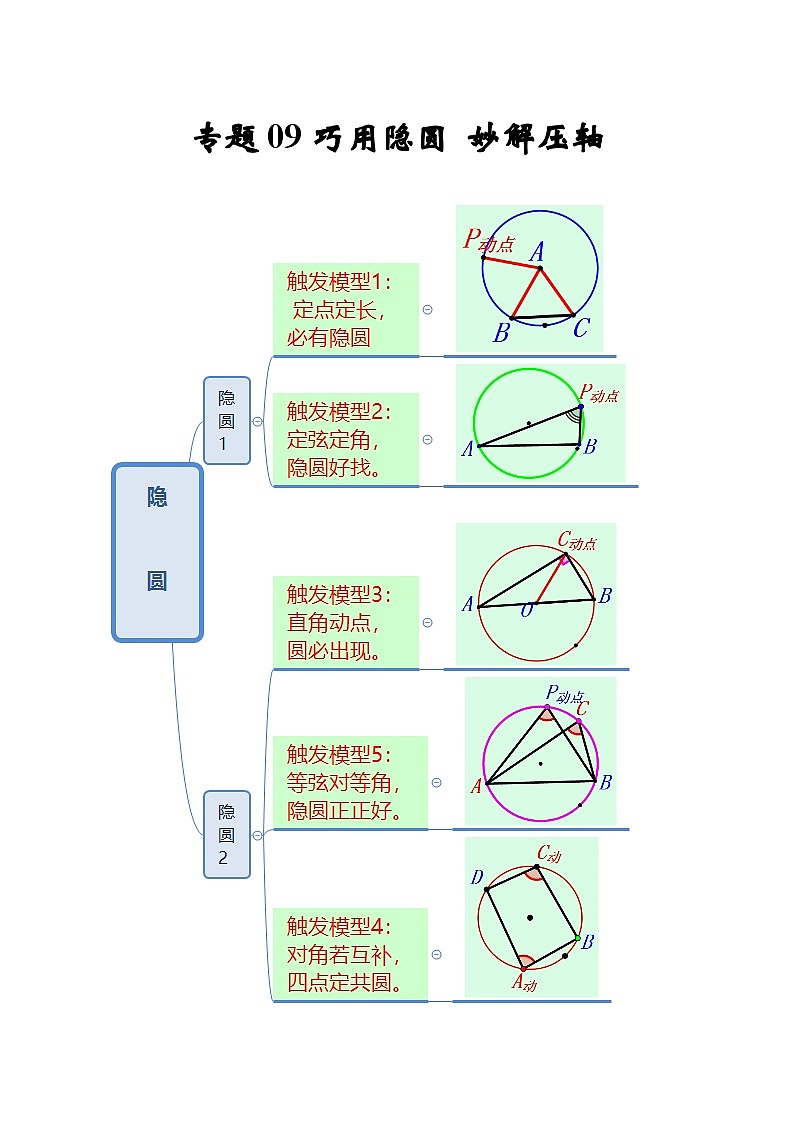
一．隐圆之定点定长
1．如图，正方形ABCD，边长为4，点P和点Q在正方形的边上运动，且PQ＝4，若点P从点B出发沿B→C→D→A的路线向点A运动，到点A停止运动；点Q从点A出发，沿A→B→C→D的路线向点D运动，到达点D停止运动．它们同时出发，且运动速度相同，则在运动过程中PQ的中点O所经过的路径长为 3π ．
试题分析：画出点O运动的轨迹，如图虚线部分，利用PQ的中点O所经过的路线长等于半径为2的圆周长的34求解即可．
答案详解：解：画出点O运动的轨迹，如图虚线部分，
则点P从B到A的运动过程中，PQ的中点O所经过的路线长等于2π×2×34=3π，
所以答案是：3π．
2．已知：如图，在正方形ABCD中，E、F分别是AD、CD的中点．
（1）线段AF与BE有何关系．说明理由；
（2）延长AF、BC交于点H，则B、D、G、H这四个点是否在同一个圆上．说明理由．
试题分析：（1）证明△ABE≌△DAF，证据全等三角形的对应边相等，以及直角三角形的两锐角互余即可证明AF相等且互相垂直；
（2）证明△ADF≌△HCF，依据直角三角形斜边上的中线等于斜边的一半，即可证得B，C，D，H四点到C的距离相等，即可证得四点共圆．
答案详解：解：（1）AF＝BE且AF⊥BE．
证明：∵E、F分别是AD、CD的中点，
∴AE=12AD，DF=12CD
∴AE＝DF
又∵∠BAD＝∠D＝90°，AB＝AD
∴△ABE≌△DAF
∴AF＝BE，∠AEB＝∠AFD
∵在直角△ADF中，∠DAF+∠AFD＝90°
∴∠DAF+∠AEB＝90°
∴∠AGE＝90°
∴AF⊥BE
（2）连接CG．
∵DF＝CF，∠D＝∠FCH＝90°，∠AFD＝∠HFC
∴△ADF≌△HCF
∴BC＝AD＝CH＝CD，
在直角△BGH中，BC＝CH，
∴GC=12BH
∴CB＝CG＝CD＝CH，
∴B，G，D，H在以C为圆心、BC长为半径的圆上．
二．隐圆之定弦定角
3．在△ABC中，AB＝4，∠C＝45°，则2AC+BC的最大值为 410 ．
试题分析：过点B作BD⊥AC于点D，则△BCD为等腰直角三角形，设BD＝CD＝a，延长AC至点F，使得CF＝a，则可求出tan∠AFB，作△ABF的外接圆⊙O，过点O作OE⊥AB于点E，则AE=12AB＝2，∠AOE＝∠AFB，则可利用tan∠AOE求出OE、OA，最后利用三角形三边关系即可求出2AC+BC的最大值为2（OA+OF），计算即可．
答案详解：解：过点B作BD⊥AC于点D，
∵∠C＝45°，
∴△BCD为等腰直角三角形，
∴BD＝CD，
设BD＝CD＝a，延长AC至点F，使得CF＝a，
∵tan∠AFB=a2a=12，
作△ABF的外接圆⊙O，过点O作OE⊥AB于点E，则AE=12AB＝2，∠AOE＝∠AFB，
∴tan∠AOE=12，
∴OE＝4，OA=22+42=25，
∴2AC+BC=2（AC+22BC）=2（AC+CF）=2AF≤2（OA+OF），
∴2AC+BC的最大值为2×45=410．
所以答案是：410．
4．如图，在矩形ABCD中，AD＝5，AB＝33，点E在AB上，AEEB=12，在矩形内找一点P，使得∠BPE＝60°，则线段PD的最小值为（ ）
A．27−2B．213−4C．4D．23
试题分析：如图，在BE的上方，作△OEB，使得OE＝OB，∠EOB＝120°，连接OD，过点O作OQ⊥BE于Q，OJ⊥AD于J．证明点P的运动轨迹是以O为圆心，OE为半径的⊙O，推出当点P落在线段OD上时，DP的值最小，想办法求出OD，OP，可得结论．
答案详解：解：如图，在BE的上方，作△OEB，使得OE＝OB，∠EOB＝120°，连接OD，过点O作OQ⊥BE于Q，OJ⊥AD于J．
∵∠BPE=12∠EOB，
∴点P的运动轨迹是以O为圆心，OE为半径的⊙O，
∴当点P落在线段OD上时，DP的值最小，
∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝33，AE：EB＝1：2，
∴BE＝23，
∵OE＝OB，∠EOB＝120°，OQ⊥EB，
∴EQ＝BQ=3，∠EOQ＝∠BOQ＝60°，
∴OQ＝1，OE＝2，
∵OJ⊥AD，OQ⊥AB，
∴∠A＝∠AJO＝∠AQO＝90°，
∴四边形AQOJ是矩形，
∴AJ＝OQ＝1，
JO＝AQ＝23，
∵AD＝5，
∴DJ＝AD﹣AJ＝4，
∴OD=JD2+OJ2=42+(23)2=27，
∴PD的最小值＝OD﹣OP＝27−2，
所以选：A．
5．问题提出
（1）如图①，已知△ABC为边长为2的等边三角形，则△ABC的面积为 3 ；
问题探究
（2）如图②，在△ABC中，已知∠BAC＝120°，BC＝63，求△ABC的最大面积；
问题解决
（3）如图③，某校学生礼堂的平面示意为矩形ABCD，其宽AB＝20米，长BC＝24米，为了能够监控到礼堂内部情况，现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测，并且要求能观测到礼堂前端墙面AB区域，同时为了观测效果达到最佳，还需要从点M出发的观测角∠AMB＝45°，请你通过所学知识进行分析，在墙面CD区域上是否存在点M满足要求？若存在，求出MC的长度；若不存在，请说明理由．
试题分析：（1）作AD⊥BC于D，由勾股定理求出AD的长，即可求出面积；
（2）作△ABC的外接圆⊙O，可知点A在BC上运动，当A'O⊥BC时，△ABC的面积最大，求出A'H的长，从而得出答案；
（3）以AB为边，在矩形ABCD的内部作一个等腰直角三角形AOB，且∠AOB＝90°，过O作HG⊥AB于H，交CD于G，利用等腰直角三角形的性质求出OA，OG的长，则以O为圆心，OA为半径的圆与CD相交，从而⊙O上存在点M，满足∠AMB＝45°，此时满足条件的有两个点M，过M1作M1F⊥AB于F，作EO⊥M1F于E，连接OF，利用勾股定理求出OE的长，从而解决问题．
答案详解：解：（1）作AD⊥BC于D，
∵△ABC是边长为2的等边三角形，
∴BD＝1，
∴AD=AB2−BD2=3，
∴△ABC的面积为12×2×3=3，
所以答案是：3；
（2）作△ABC的外接圆⊙O，
∵∠BAC＝120°，BC＝63，
∴点A在BC上运动，
当A'O⊥BC时，△ABC的面积最大，
∴∠BOA'＝60°，BH＝CH＝33，
∴OH＝3，OB＝6，
∴A'H＝OA'﹣OH＝6﹣3＝3，
∴△ABC的最大面积为12×63×3＝93；
（3）存在，以AB为边，在矩形ABCD的内部作一个等腰直角三角形AOB，且∠AOB＝90°，
过O作HG⊥AB于H，交CD于G，
∵AB＝20米，
∴AH＝OH＝10米，OA＝102米，
∵BC＝24米，
∴OG＝14米，
∵102＞14，
∴以O为圆心，OA为半径的圆与CD相交，
∴⊙O上存在点M，满足∠AMB＝45°，此时满足条件的有两个点M，
过M1作M1F⊥AB于F，作EO⊥M1F于E，连接OF，
∴EF＝OH＝10米，OM1＝102米，
∴EM1＝14米，
∴OE=OM12−M1E2=2米，
∴CM1＝BF＝8米，
同理CM2＝BH+OE＝10+2＝12（米），
∴MC的长度为8米或12米．
三．隐圆之直角动点
6．如图，在矩形ABCD中，AB＝8，BC＝5，P是矩形内部一动点，且满足∠PAB＝∠PBC，则线段CP的最小值是 41−4 ．
试题分析：首先证明点P在以AB为直径的⊙O上，连接OC与⊙O交于点P，此时PC最小，利用勾股定理求出OC即可解决问题．
答案详解：解：∵∠ABC＝90°，
∴∠ABP+∠PBC＝90°，
∵∠PAB＝∠PBC，
∴∠BAP+∠ABP＝90°，
∴∠APB＝90°，
∴OP＝OA＝OB（直角三角形斜边中线等于斜边一半），
∴点P在以AB为直径的⊙O上，连接OC交⊙O于点P，此时PC最小，
∵在矩形ABCD中，AB＝8，BC＝5，
在RT△BCO中，∵∠OBC＝90°，BC＝5，OB＝4，
∴OC=BO2+BC2=41，
∴PC＝OC﹣OP=41−4．
∴PC最小值为41−4．
所以答案是：41−4．
7．如图，等边△ABC的边长为6，D为BC边上的中点，P为直线BC上方的一个动点，且满足∠PAD＝∠PDB，则线段CP长的最大值为 37+332． ．
试题分析：首先证明点P在以AD为直径的⊙O上，连接OC，延长CO交⊙O于点P，此时PC最大，利用勾股定理求出OC即可解决问题．
答案详解：解：∵等边△ABC的边长为6，D为BC边上的中点，
∴∠ADB＝90°，
∴∠ADP+∠PDB＝90°，
∵∠PAD＝∠PDB
∴∠DAP+∠ADP＝90°，
∴∠APD＝90°，
∴点P在以AD为直径的⊙O上，连接OC，延长CO交⊙O于点P，此时PC最大，
在Rt△CDO中，∵∠ODC＝90°，DC=12BC＝3，OD=12AD=332，
∴OC=OD2+CD2=372，
∴PC＝OC+OP=372+332=37+332．
∴CP长的最大值为37+332．
所以答案是37+332．
8．如图，在矩形ABCD中，AB＝8，BC＝6，点P在矩形的内部，连接PA，PB，PC，若∠PBC＝∠PAB，则PC的最小值是（ ）
A．6B．73−3C．213−4D．413−4
试题分析：首先证明∠PAB+∠PBA＝90°，得∠APB＝90°，则点P在以AB为直径的圆上运动，设圆心为O，连接OC交⊙O于P，此时PC最小，利用勾股定理求出OC的长即可．
答案详解：解：∵四边形ABCD是矩形，
∴∠ABC＝90°，
∴∠ABP+∠PBC＝90°，
∵∠PBC＝∠PAB，
∴∠PAB+∠PBA＝90°，
∴∠APB＝90°，
∴点P在以AB为直径的圆上运动，设圆心为O，连接OC交⊙O于P，此时PC最小，
∵OC=OB2+BC2=42+62=213，
∴PC的最小值为213−4，
所以选：C．
四．隐圆之对角互补。
9．如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠ACD＝30°，AD＝2，E是AC的中点，连接DE，则线段DE长度的最小值为 3−1 ．
试题分析：先判断出A、B、C、D四点共圆，且圆心为BD中点，再连接AO、CO，取AO中点F，连接EF，DF，利用圆周角定理及等边三角形的判定可得到△OAD为等边三角形，进而得到半径长、DF、EF，最后利用三角形三边关系即可求出DE最小值．
答案详解：解：∵∠BAD＝∠BCD＝90°，
∴A、B、C、D四点共圆，且BD为直径，取BD中点O，则圆心为点O，
连接AO、CO，取AO中点F，连接EF，DF，
∵∠ACD＝30°，
∴∠AOD＝60°，
∵OA＝OD，
∴△OAD为等边三角形，
∴OA＝OD＝OC＝AD＝2，
∴∠AFD＝90°，则DF=3，
∵EF是△AOC的中位线，
∴EF=12OC＝1，
在△DEF中，DF﹣EF≤DE，
∴当D、E、F三点共线时，DE取到最小，最小值为3−1．
∴DE的最小值为3−1．
10．如图，四边形ABCD中，∠ABC＝∠ACD＝∠ADC＝45°，△DBC的面积为8，则BC长为 4 ．
试题分析：如图，作DH⊥BC交BC的延长线于H，取CD的中点O，连接OA，OB．由对角互补可证明A，C，H，D四点共圆，利用全等三角形的性质证明BC＝DH，即可解决问题．
答案详解：解：如图，作DH⊥BC交BC的延长线于H，取CD的中点O，连接OA，OB．
∵DH⊥BH，
∴∠DHC＝90°，
∴四边形DACH对角互补，
∴A，C，H，D四点共圆，
∵∠DAC＝90°，CO＝OD，
∴OA＝OD＝OC＝OH，
∴A，C，H，D四点在以O为圆心的圆上，
∵AC＝AD，
∴∠CHA＝∠AHD＝45°，（没有学习四点共圆，可以这样证明：过点A作AM⊥DH于M，过点A作AN⊥BH于N，证明△AMD≌△ANC，推出AM＝AN，推出AH平分∠MHN即可）
∵∠ABC＝45°，
∴∠BAH＝90°，
∴BA＝AH，
∵∠BAH＝∠CAD＝90°，
∴∠BAC＝∠HAD，
∵AC＝AD，AB＝AH，
∴△BAC≌△HAD（SAS），
∴BC＝DH，
∴S△BCD=12×BC×DH=12×BC2＝16，
∴BC＝4或﹣4（舍弃），
所以答案是4．
11．问题提出：
（1）如图①，半圆O的直径AB＝10，点P是半圆O上的一个动点，则△PAB的面积最大值是 25 ．
问题探究：
（2）如图②，在边长为10的正方形ABCD中，点G是BC边的中点，E、F分别是AD和CD边上的点，请探究并求出四边形BEFG的周长的最小值．
问题解决：
（3）如图③，四边形ABCD中，AB＝AD＝6，∠BAD＝60°，∠BCD＝120°，四边形ABCD的周长是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．
试题分析：（1）如图1，点P运动至半圆O的中点时，底边AB上的高最大，即P'O＝r＝5，求出此时△P'AB的面积即可；
（2）如图2，作点G关于CD的对称点G′，作点B关于AD的对称点B′，连接B′G′，B'E，FG'，根据两点之间线段最短即可解决问题；
（3）如图3，连接AC、BD，在AC上取一点，使得DM＝DC．首先证明AC＝CD+CB，再证明当AC为△ABC的外接圆的直径时，四边形ABCD的周长最大．
答案详解：解：（1）如图1，点P运动至半圆O的中点时，底边AB上的高最大，即P'O＝r＝5，
此时△PAB的面积最大值，
∴S△P'AB=12×10×5＝25，
所以答案是：25；
（2）如图2，作点G关于CD的对称点G′，作点B关于AD的对称点B′，连接B′G′，B'E，FG'，
∵EB＝EB′，FG＝FG′，
∴BE+EF+FG+BG＝B′E+EF+FG′+BG，
∵EB′+EF+FG′≥B′G′，
∴四边形BEFG的周长的最小值＝BG+B′G′，
∵BG=12BC＝5，BB′＝20，BG′＝15，
∴B′G′=BG'2+BB'2=152+202=25，
∴四边形BEFG的周长的最小值为30．
（3）如图3，连接AC、BD，在AC上取一点，使得DM＝DC．
∵∠DAB＝60°，∠DCB＝120°，
∴∠DAB+∠DCB＝180°，
∴A、B、C、D四点共圆，
∵AD＝AB，∠DAB＝60°，
∴△ADB是等边三角形，
∴∠ABD＝∠ADB＝60°，
∴∠ACD＝∠ADB＝60°
∵DM＝DC，
∴△DMC是等边三角形，
∴∠ADB＝∠MDC＝60°，CM＝DC，
∴∠ADM＝∠BDC，
∵AD＝BD，
∴△ADM≌△BDC（SAS），
∴AM＝BC，
∴AC＝AM+MC＝BC+CD，
∵四边形ABCD的周长＝AD+AB+CD+BC＝AD+AB+AC，
∵AD＝AB＝6，
∴当AC最大时，四边形ABCD的周长最大，
∴当AC为△ABC的外接圆的直径时，四边形ABCD的周长最大，
∵6AC=sin60°，
∴AC的最大值＝43，
∴四边形ABCD的周长最大值为12+43．
五．隐圆综合
12．阅读下列材料，回答问题．
材料：求圆外一定点到圆上距离最小值是安徽省中考数学较为常见的一种题型，此类题型试题有时出题者将圆隐藏，故又称为“隐圆问题”．解决这类问题，关键是要找到动点的运动轨迹，即该动点是绕哪一个定点旋转，且能保持旋转半径不变．从而找到动点所在的隐藏圆，进而转换成圆外一点到圆心的距离减半径，求得最小值．
解决问题：
（1）如图①，圆O的半径为1，圆外一点A到圆心的距离为3，圆上一动点B，当A、O、B满足条件 点B在线段AO上 时，AB有最小值为 2 ．
（2）如图②，等腰△ABC两腰长为5，底边长为6，以A为圆心，2为半径作圆，圆上动点P到BC的距离最小值为 2 ．
（3）如图③，OA⊥OB，P、Q分别是射线OA、OB上两个动点，C是线段PQ的中点，且PQ＝4，则在线段PQ滑动的过程中，求点C运动形成的路径长，并说明理由．
（4）如图④，在矩形ABCD中，AB＝4，AD＝8，点E是AB中点，点F是BC上一点，把△BEF沿着EF翻折，点B落在点B'处，求DB'的最小值，并说明理由．
（5）如图⑤，在△ABC中，AB＝10，AC＝8，BC＝6，以边AB中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，求PQ长的最小值，并说明理由．
试题分析：（1）如图①，连接OA，OB，OA，由三角形的三边关系可得AB≤AO﹣BO，则当点B在线段AO上时，AB有最小值＝3﹣1＝2；
（2）如图②中，过点A作AH⊥BC于H，交⊙A于P，此时点P到BC的距离最小．
（3）利用直角三角形斜边中线的性质，的长OC＝2，再利用弧长公式求解即可．
（4）如图④中，连接DE，DB′．利用勾股定理求出DE，根据DB′≥DE﹣EB′，可得DB′≥217−2，由此可得结论．
（5）当O、Q、P三点共线且OP⊥BC时，PQ有最小值，设AC与圆的切点为D，连接OD，分别利用三角形中位线定理可求得OD和OP的长，则可求得PQ的最小值．
答案详解：解：（1）如图①，连接OA，OB，OA，
在△ABO中，AB≤AO﹣BO，
当点B在线段AO上时，AB有最小值＝3﹣1＝2，
所以答案是：点B在线段AO上，2．
（2）如图②中，过点A作AH⊥BC于H，交⊙A于P，此时点P到BC的距离最小．
∵AB＝AC＝5，AH⊥BC，
∴BH＝CH=12BC＝3，
∴AH=AB2−BH2=52−32=4，
∵PA＝2，
∴PH＝AH﹣AP＝2，
∴圆上动点P到BC的距离最小值为2，
所以答案是：2．
（3）如图③中，连接OC．
∵∠POQ＝90°，PQ＝4，PC＝CQ，
∴OC=12PQ＝2，
∴点C的运动轨迹是圆弧，运动路径的长=90⋅π⋅2180=π．
（4）如图④中，连接DE，DB′．
∵四边形ABCD是矩形，
∴∠A＝90°，
∵AE＝EB＝2，AD＝8，
∴DE=AE2+AD2=22+82=217，
∵BE＝EB′＝2，
∴DB′≥DE﹣EB′，
∴DB′≥217−2，
∴DB′的最小值为217−2．
（5）当O、Q、P三点共线且OP⊥BC时，PQ有最小值，设AC与圆的切点为D，连接OD，如图⑤中，
∵AC为圆的切线，
∴OD⊥AC，
∵AC＝8，BC＝6，AB＝10，
∴AC2+BC2＝AB2，
∴∠ACB＝90°，
∴OD∥BC，且O为AB中点，
∴OD为△ABC的中位线，
∴OD=12BC＝3，
同理可得PO=12AC＝4，
∴PQ＝OP﹣OQ＝4﹣3＝1，
∴PQ的最小值为1．