
新高考数学一轮复习考点精讲讲练学案 平面向量的线性运算(含解析)
展开1. 向量的线性运算
2、进行向量的线性运算时,要尽可能转化到平行四边形或三角形中,选用从同一顶点出发的基本向量或首尾相接的向量,运用向量加、减法运算及数乘运算来解决.
3、加法运算的推广
(1)加法运算的推广:eq \(A1A2,\s\up6(→))+eq \(A2A3,\s\up6(→))+…+An-1An=eq \(A1An,\s\up6(→)).
(2)向量三角不等式:||a|-|b||≤|a±b|≤|a|+|b|. 两向量不共线时,可由“三角形中任意两边之和大于第三边,任意两边之差小于第三边”知“<”成立;两向量共线时,可得出“=”成立(分同向、反向两种不同情形).
4、线性运算重要结论
(1)若P为线段AB的中点,O为平面内任一点,则eq \(OP,\s\up6(→))=eq \f(1,2)(eq \(OA,\s\up6(→))+eq \(OB,\s\up6(→))).
(2)若G为△ABC的重心,则eq \(GA,\s\up6(→))+eq \(GB,\s\up6(→))+eq \(GC,\s\up6(→))=0.
(3)若eq \(OA,\s\up6(→))=λeq \(OB,\s\up6(→))+μeq \(OC,\s\up6(→))(λ,μ为实数),则点A,B,C共线的充要条件是λ+μ=1.
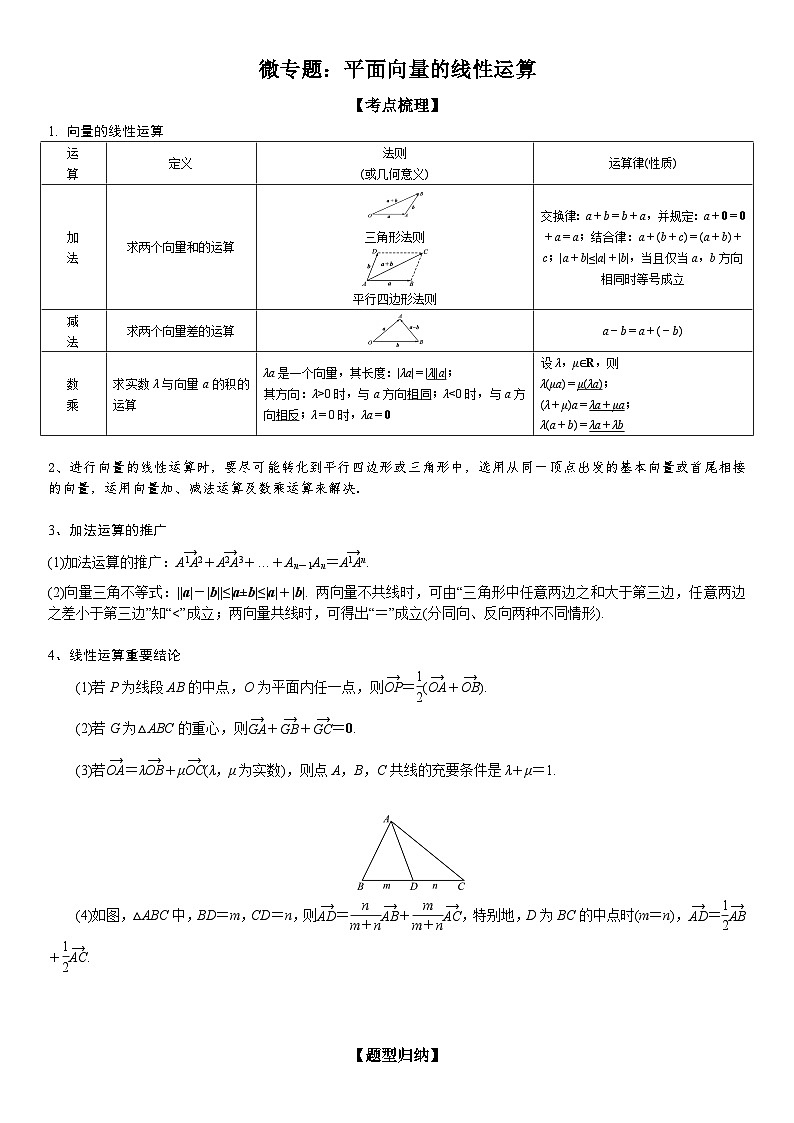
(4)如图,△ABC中,BD=m,CD=n,则eq \(AD,\s\up6(→))=eq \f(n,m+n)eq \(AB,\s\up6(→))+eq \f(m,m+n)eq \(AC,\s\up6(→)),特别地,D为BC的中点时(m=n),eq \(AD,\s\up6(→))=eq \f(1,2)eq \(AB,\s\up6(→))+eq \f(1,2)eq \(AC,\s\up6(→)).
【题型归纳】
题型一:平面向量的加法
1.正方形 中, 点 是 的中点, 点 是 的一个三等分点, 那么 ( )
A.
B.
C.
D.
2.已知等腰的直角边长为1,为斜边上一动点,则的最小值为( )
A.B.C.D.
3.如图,在正方形网格中,向量,满足,则( )
A.B.
C.D.
题型二: 平面向量的减法
4.如图,是两条对角线的交点,则下列等式成立的是( )
A.B.
C.D.
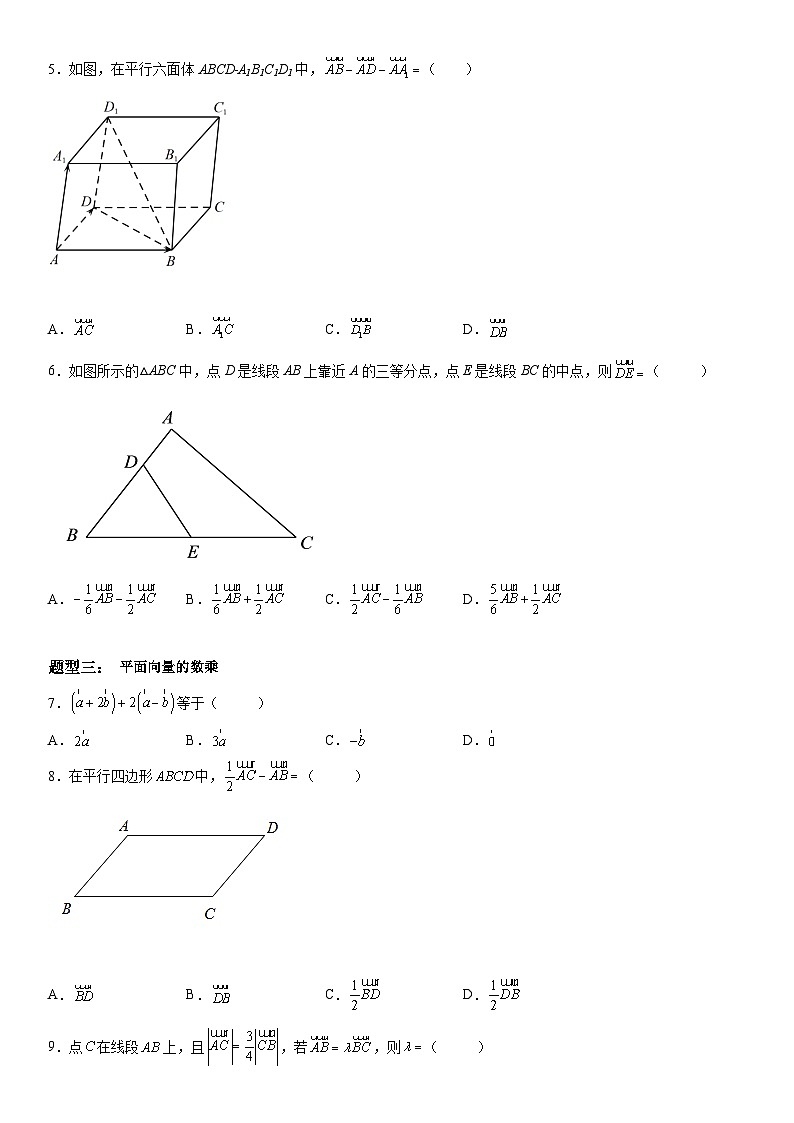
5.如图,在平行六面体ABCD﹣A1B1C1D1中,( )
A.B.C.D.
6.如图所示的△ABC中,点D是线段AB上靠近A的三等分点,点E是线段BC的中点,则( )
A.B.C.D.
题型三: 平面向量的数乘
7.等于( )
A.B.C.D.
8.在平行四边形中,( )
A.B.C.D.
9.点在线段上,且,若,则( )
A.B.C.D.
题型四:向量的线性运算的几何应用
10.如图,在中,己知,则( )
A.B.
C.D.
11.如图,在中,,则( )
A.B.C.D.
12.如图,分别是边上的中线,与交于点F,设,,,则等于( )
A.B.C.D.
【双基达标】
13.如图所示,向量等于( )
A.B.
C.D.
14.如图所示,等腰梯形中,,点为线段上靠近的三等分点,点为线段的中点,则( )
A.B.
C.D.
15.化简的结果为( )
A.B.C.D.
16.化简( )
A.B.C.D.
17.已知点为所在平面内一点,若动点满足,则点一定经过的( )
A.外心B.内心C.垂心D.重心
18.在正方形中,( )
A.B.C.D.
19.已知向量,且不是方向相反的向量,则的取值范围是( )
A.B.
C.D.
20.如图,是的边中点,则向量=( )
A.B.
C.D.
21.若,,则的取值范围是( )
A.B.
C.D.
22.在△中,为边上的中线,为的中点,则
A.B.
C.D.
23.若M为△ABC的边AB上一点,且则=( )
A.B.C.D.
24.已知非零向量,满足,则“”是“”的( )
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分又不必要条件
25.在矩形ABCD中,,则( )
A.B.C.D.
26.在平行四边形中,,若,则=( )
A.B.C.D.3
27.在中,角所对的边分别为,且点满足,若,则的最大值为( )
A.B.C.D.
28.在中,若点满足,点为的中点,则( )
A.B.
C.D.
29.向量,互为相反向量,已知,则下列结论正确的是( )
A.B.为实数0C.与方向相同D.
30.已知非零平面向量,,,下列结论中正确的是( )
(1)若,则;(2)若,则
(3)若,则(4)若,则或
A.(1)(2)B.(2)(3)C.(3)(4)D.(2)(3)(4)
【高分突破】
单选题
31.我国东汉末数学家赵夾在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若,,,则=( )
A.B.
C.D.
32.如图,在△中,点M是上的点且满足,N是上的点且满足,与交于P点,设,则( )
A.B.
C.D.
33.如图,四边形ABCD是平行四边形,则( )
A.B.C.D.
34.化简下列各式:①;②;③;④.其中结果为的个数是( )
A.1B.2C.3D.4
35.已知点P是△ABC所在平面内点,有下列四个等式:
甲:; 乙:;
丙:; 丁:.
如果只有一个等式不成立,则该等式为( )
A.甲B.乙C.丙D.丁
36.如图,点在的内部,,是边,的中点(,,三点不共线),,,则向量与的夹角大小为( )
A.105°B.120°C.135°D.150°
37.如图,向量,,,则向量可以表示为( )
A.B.C.D.
二、多选题
38.在平面直角坐标系中,以,,为顶点构造平行四边形,下列各项中能作为平行四边形第四个顶点坐标的是( )
A.B.C.D.
39.下列各式中,结果为零向量的是( )
A.B.
C.D.
40.下列说法错误的是( )
A.若,则存在唯一实数使得
B.两个非零向量,,若,则与共线且反向
C.已知,,且与的夹角为锐角,则实数的取值范围是
D.在中,,则为等腰三角形
41.等边三角形中,,AD与BE交于F,则下列结论正确的是( )
A.B.
C.D.
三、填空题
42.设为所在平面上一点,且满足,若的面积为2,则面积为_______________.
43.在菱形中,,,,则___________.
44.如图,在矩形ABCD中,M,N分别为线段BC,CD的中点,若,,则的值为________.
45.点为内一点,,则的面积之比是___________.
46.如图,在平面四边形中,.若点为边上的动点,则的最小值为_________.
47.在直角坐标系中,为原点,O、A、B不共线,,则________
四、解答题
48.如图所示,是的一条中线,点满足,过点的直线分别与射线,射线交于,两点.
(1)求证:;
(2)设,,,,求的值;
(3)如果是边长为的等边三角形,求的取值范围.
49.如图,已知正方形的边长等于单位长度1,,,,试着写出向量.
(1);
(2),并求出它的模.
50.如图,矩形与矩形全等,且.
(1)用向量与表示;
(2)用向量与表示.
51.已知中,过重心G的直线交边于P,交边于Q,设的面积为,的面积为,,.
(1)求;
(2)求证:.
(3)求的取值范围.
52.(1)化简:.
(2)已知向量为,未知向量为向量,满足关系式,求向量.
运
算
定义
法则
(或几何意义)
运算律(性质)
加
法
求两个向量和的运算
三角形法则
平行四边形法则
交换律:a+b=b+a,并规定:a+0=0+a=a;结合律:a+(b+c)=(a+b)+c;|a+b|≤|a|+|b|,当且仅当a,b方向相同时等号成立
减
法
求两个向量差的运算
a-b=a+(-b)
数
乘
求实数λ与向量a的积的运算
λa是一个向量,其长度:|λa|=|λ||a|;
其方向:λ>0时,与a方向相同;λ<0时,与a方向相反;λ=0时,λa=0
设λ,μ∈R,则
λ(μa)=μ(λa);
(λ+μ)a=λa+μa;
λ(a+b)=λa+λb
参考答案
1.D
【解析】
【分析】
根据平面向量的线性运算结合图象即可得解.
【详解】
解:∵点E是DC的中点,点F是BC的一个三等分点,
∴.
故选:D.
2.A
【解析】
【分析】
由向量的加法运算结合三角形的性质求解即可.
【详解】
,显然当为斜边中点时,,此时最小为,即的最小值为.
故选:A.
3.C
【解析】
【分析】
由向量加减法运算法则,得到所求向量为,再由向量减法的三角形法则,以及向量数乘运算,计算答案.
【详解】
由题意得,
故选:C.
4.D
【解析】
【分析】
根据向量的加减法的三角形法则及平行四边形的性质即可求解.
【详解】
由向量减法的运算可得,
又因为四边形为平行四边形,所以.
故选:D.
5.C
【解析】
【分析】
根据已知条件,结合向量的相反向量、加减法法则,即可求解.
【详解】
解:由题意可得,在平行六面体ABCD﹣A1B1C1D1中,,,所以
.
故选:C.
6.B
【解析】
【分析】
依题意可得,,根据平面向量的加减运算可得.
【详解】
由已知可得,,
所以.
故选:B.
7.B
【解析】
【分析】
利用向量的线性运算求解即可.
【详解】
依题意得:
,
故选:B.
8.C
【解析】
【分析】
利用图形进行向量的加减、数乘运算,求出答案
【详解】
连接AC,BD相交于点O,则
故选:C
9.D
【解析】
【分析】
利用平面向量共线定理进行求解
【详解】
不妨设,则,
因为点在线段上,则,
故选:D
10.C
【解析】
【分析】
根据平面向量的线性运算即可得出答案.
【详解】
解:因为,
所以,
故选:C.
11.A
【解析】
【分析】
依题意可得,再根据平面向量线性运算法则计算可得;
【详解】
解:因为,所以,
所以
.
故选:A
12.D
【解析】
【分析】
根据已知有是的重心,由重心的性质及向量加法、数乘的几何意义,用、表示,即可得结果.
【详解】
由题意,是的重心,
=,
,故.
故选:D
13.C
【解析】
把,代入中化简即可.
【详解】
解:.
故选:C
14.A
【解析】
【分析】
利用平面向量的加法和减法以及平面向量的基本定理求解.
【详解】
,
,
,
,
故选:A.
15.A
【解析】
【分析】
由向量的加减运算法则即可求解.
【详解】
解:,
故选:A.
16.B
【解析】
【分析】
根据向量加法法则即可计算.
【详解】
.
故选:B.
17.D
【解析】
【分析】
取的中点,由,得,从而可得与共线,得直线与直线重合,进而得结论
【详解】
解:取的中点,则,
因为,
所以,
所以与共线,即直线与直线重合,
所以直线一定过的重心,
故选:D
18.C
【解析】
【分析】
根据平面向量加减运算法则计算可得.
【详解】
解:.
故选:C.
19.B
【解析】
【分析】
直接由求解即可.
【详解】
由已知必有,则所求的取值范围是.
故选:B.
20.D
【解析】
【分析】
利用向量的加、减以及数乘运算即可求解.
【详解】
.
故选:D
21.C
【解析】
【分析】
利用向量模的三角不等式可求得的取值范围.
【详解】
因为,所以,,即.
故选:C.
22.A
【解析】
【分析】
分析:首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.
【详解】
根据向量的运算法则,可得
,
所以,故选A.
【点睛】
该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.
23.A
【解析】
先用向量,表示向量,再转化为用,表示即可得答案.
【详解】
解:根据题意做出图形,如图,
所以,
所以.
故选:A.
【点睛】
关键点睛:解题关键在于利用向量的线性运算进行求解,属于基础题
24.C
【解析】
由非零向量,满足,推导出“” “”,从而得到“”是“”的充分必要条件.
【详解】
非零向量,满足,
“”, “”,
“”, ,
,
,
“”是“”的充分必要条件.
故选:C..
【点睛】
该题考查充分条件、必要条件、充要条件的判断,考查向量的性质等基础知识,考查运算求解能力,属于基础题目.
25.C
【解析】
由平面向量的线性运算可得,再由平面向量数量积的运算法则计算即可得解.
【详解】
由题意作出图形,如下图,
所以
.
故选:C.
26.B
【解析】
由题意分析可知,四边形为菱形且,然后求解.
【详解】
,则平分,则四边形为菱形.
且,由,则,
故选:B.
【点睛】
关键点睛:本题考查向量的综合运用,解题的关键是要注意为上的单位向量,考查学生的逻辑推理能力与运算能力,属于基础题.
27.A
【解析】
【分析】
利用向量知识可得,两边平方可得,再利用不等式知识可求得结果.
【详解】
因为,所以,所以,
所以,
所以,整理得,
所以,
因为,所以,
所以,解得.
所以的最大值为
故选:A
【点睛】
关键点点睛:将向量条件化为,利用向量数量积的运算律运算得到是解题关键.
28.A
【解析】
利用平面向量的线性运算和平面向量基本定理即可求解.
【详解】
.
故选:A
29.D
【解析】
【分析】
根据相反向量的定义,即可判断选项.
【详解】
向量,互为相反向量,则,模相等、方向相反,所以,故A错误;
,故B错误;与方向相反,故C错误;,故D正确.
故选:D.
30.B
【解析】
根据向量的数量积运算,以及向量模的计算公式,逐项判断,即可得出结果.
【详解】
已知非零平面向量,,,
(1)若,则,所以或,即(1)错;
(2)若,则与同向,所以,即(2)正确;
(3)若,则,所以,则;即(3)正确;
(4)若,则,所以,不能得出向量共线,故(4)错;
故选:B.
【点睛】
本题主要考查向量数量积的运算,考查向量有关的判定,属于基础题型.
31.B
【解析】
【分析】
根据给定图形,利用平面向量的加法法则列式求解作答.
【详解】
因“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,且,,,
则
,解得,所以.
故选:B
32.B
【解析】
【分析】
根据三点共线有,使、,由平面向量基本定理列方程组求参数,即可确定答案.
【详解】
,,
由,P,M共线,存在,使①,
由N,P,B共线,存在,使得②,
由①② ,故.
故选:B.
33.D
【解析】
【分析】
由平面向量的加减法法则进行计算.
【详解】
由题意得,,
所以.
故选:D.
34.B
【解析】
【分析】
根据向量的加减运算法则计算,逐一判断①②③④的正确性,即可得正确答案.
【详解】
对于①:,
对于②:,
对于③:,
对于④:,
所以结果为的个数是,
故选:B
35.B
【解析】
【分析】
先根据向量等式推导出甲中P为△ABC的重心,乙中△ABC为直角三角形,丙中P为△ABC的外心,丁中P为△ABC的垂心,故得到当△ABC为等边三角形时,三心重合,此时甲丙丁均成立,乙不成立,得到答案.
【详解】
甲:,则,故P为△ABC的重心;
乙:,则,故,即△ABC为直角三角形;
丙:点P到三角形三个顶点距离相等,故P为△ABC的外心;
丁:,则,同理可得:,即P为△ABC的垂心,
当△ABC为等边三角形时,三心重合,此时甲丙丁均成立,乙不成立,满足要求,当乙成立时,其他三个均不一定成立.
故选:B.
36.B
【解析】
由,是边,的中点,得,由可得答案.
【详解】
连接,如下图所示.
因为,是边,的中点,所以,且,所以,所以
,解得.又因为,
所以.则向量与的夹角大小为120°,
故选:B.
【点睛】
本题考查向量的线性运算,数量积.
37.C
【解析】
【分析】
利用向量加法和减法的三角形法则计算即可.
【详解】
故选:C.
38.BCD
【解析】
【分析】
依次代入四个选项的坐标,求出每种情况下四边的长度,结合对边是否平行即可选出正确答案.
【详解】
解:设第四个顶点为.
对于A选项,当点的坐标为时,,,,
.∵,,∴四边形不是平行四边形.A不正确;
对于B选项,当点坐标为时,因为,即且,
故是平行四边形,B正确;
对于C选项,当点坐标为时,因为,即且,故是平行四边形,C正确;
对于D选项,当点坐标为时,因为,即且,故是平行四边形,D正确;
故选:BCD.
39.BD
【解析】
【分析】
根据向量的加法和减法运算,对四个选项逐一计算,即可得正确答案.
【详解】
对于选项:,选项不正确;
对于选项: ,选项正确;
对于选项:,选项不正确;
对于选项:
选项正确.
故选:BD
【点睛】
本题主要考查了向量的线性运算,属于基础题.
40.AC
【解析】
【分析】
若可判断A;将已知条件两边平方再进行数量积运算可判断B;求出的坐标,根据且与不共线求出的取值范围可判断C;取的中点,根据向量的线性运算可得可判断D,进而可得正确选项.
【详解】
对于A:若满足,则实数不唯一,故选项A错误;
对于B:两个非零向量,,若,则,
所以,可得,,因为,所以,所以与共线且反向,故选项B正确;
对于C:已知,,所以,若与的夹角为锐角,则,解得:,当时,,此时与的夹角为,不符合题意,所以,所以的取值范围是,故选项C不正确;
对于D:在中,取的中点,由,得,故垂直平分,所以为等腰三角形,故选项D正确.
故选:AC.
41.AC
【解析】
【分析】
可画出图形,根据条件可得出为边的中点,从而得出选项A正确;
由可得出,进而可得出,从而得出选择B错误;
可设,进而得出,从而得出,进而得出选项C正确;
由即可得出,从而得出选项D错误.
【详解】
如图,
,为的中点,,A正确;
,,
, B错误;
设,且,,三点共线,
,解得,
,C正确;
,D错误.
故选:AC
42.3
【解析】
【分析】
由已知条件可得,令,则可得,从而可得为上靠近的三等分点,由,得∥,从而有,进而可求得答案
【详解】
解:因为,
所以,
令,则,
所以,所以为上靠近的三等分点,
因为,所以∥,
所以,
所以,
故答案为:3
43.
【解析】
【分析】
利用向量加减法的几何意义可得、,再应用向量数量积的运算律及已知条件求即可.
【详解】
由题意,.
故答案为:
44.
【解析】
【分析】
利用平面向量基本定理分别把向量,用基底{,}表示出,结合得到含有系数,的的基底表示,与直接根据向量的线性运算得到的的基底表示比较,利用向量基本定理中的分解唯一性,即可求出,的关系,进而求得结论.
【详解】
解:因为,,
所以,
又因为,
且,不共线,所以,
两式相加得,
显然,所以,
故答案为:.
45.
【解析】
【分析】
先将已知的向量关系式化为,设为中点,为中点,再根据平面向量的平行四边形法则的加法运算得出,从而可知三点共线,且,进而得出,,最后利用三角形中位线的性质和三角形面积公式,即可确定面积比.
【详解】
解:因为,所以,
设为中点,为中点,为三角形的中位线,则,
因为,
可得,所以三点共线,且,
则,,
分别设,
由图可知,,,
则,所以,而,所以,
所以,,
所以,
即的面积之比等于.
故答案为:.
46.
【解析】
【分析】
设,根据条件找出,,且与的夹角为,与的夹角为,从而根据向量的加法法则和减法的定义写出,然后表示为关于的二次函数,通过求二次函数的最小值即可解决问题.
【详解】
延长交于点,因为,所以,,
在中,,,所以,
在中,,,所以,
所以,不妨设,则,且与的夹角为,与的夹角为,
则
,
所以时,取最小值.
故答案为:.
47.0
【解析】
根据向量的线性运算求出,根据对应关系求出的值即可.
【详解】
,
,
,
,,.
故答案为:0.
48.(1)见详解
(2)3
(3)
【解析】
【分析】
(1)根据题意,结合向量加减法运算,即可证明;
(2)根据题意,用和表示, 结合,,三点共线,即可求解;
(3)根据题意,结合(1)(2)用和分别表示出和,进而可以表示出,再结合均值不等式与二次函数的最值,即可求解.
(1)
证明:因,所以,又因为的中点,所以,所以.
(2)
因,,,,所以,,又因,所以,又因,,三点共线,所以,即.
(3)
设,,,,由(1)(2)可知,,即.
因,,
所以
,
又因是边长为的等边三角形,
所以,
令,因,即,当且仅当时,等号成立,所以.
因此,
又因,所以,所以.
49.(1);(2),2.
【解析】
【分析】
(1)由即得解;
(2)由即得解.
【详解】
(1);
(2).
∴.
【点睛】
本题主要考查向量的加法法则,考查向量的模的计算,意在考查学生对这些知识的理解掌握水平.
50.(1)
(2)
【解析】
【分析】
(1)平面向量基本定理,利用向量的加减与数乘运算法则进行求解;(2)建立平面直角坐标系,利用坐标运算进行解答.
(1)
.
(2)
以A为坐标原点,AE所在直线为x轴,AB所在直线为y轴建立如图所示的平面直角坐标系,
设,因为矩形与矩形全等,且,
所以,则,,,,,
所以,,,故.
51.(1);(2)证明见解析;(3)
【解析】
(1)延长交于D,则D为BC中点,可得,,即可求出;
(2)设,可得,,可得,即可建立关系求得;
(3)可得,再根结合的范围求出.
【详解】
(1)延长交于D,则D为BC中点,
,
G是重心,,
;
(2)设,
,,
,,
三点共线,
则存在,使得,即,
即,
,整理得,
即,即,即;
(3)由(2),,
,
,,可知,
,
,,
则当时,取得最小值,当时,取得最大值,
,则的取值范围为.
【点睛】
本题考查平面向量的线性运算,考查基本定理和共线定理的应用,考查面积公式的应用,属于较难题.
52.(1) ;(2) ,.
【解析】
【分析】
(1)利用向量的加减、数乘运算化简即可.
(2)联立题设向量的线性关系式,可得关于的线性表达式,进而求关于的线性表达式.
【详解】
(1).
(2)由①,②,
∴①+②,得,代入①得,即.
∴,.
新高考数学一轮复习考点精讲讲练学案 直线的对称问题(含解析): 这是一份新高考数学一轮复习考点精讲讲练学案 直线的对称问题(含解析),共37页。学案主要包含了考点梳理,题型归纳,双基达标,高分突破等内容,欢迎下载使用。
新高考数学一轮复习考点精讲讲练学案 圆的切线方程(含解析): 这是一份新高考数学一轮复习考点精讲讲练学案 圆的切线方程(含解析),共42页。学案主要包含了考点梳理,题型归纳,双基达标,高分突破等内容,欢迎下载使用。
新高考数学一轮复习考点精讲讲练学案 求导运算(含解析): 这是一份新高考数学一轮复习考点精讲讲练学案 求导运算(含解析),共28页。学案主要包含了考点梳理,题型归纳,双基达标,高分突破等内容,欢迎下载使用。