新高考数学二轮复习讲义第二讲常用逻辑用语 （含解析）

这是一份新高考数学二轮复习讲义第二讲常用逻辑用语 （含解析），共17页。
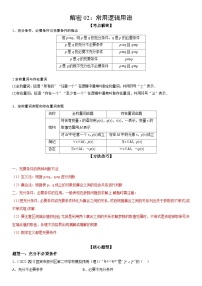
1．充分条件、必要条件与充要条件的概念
2．全称命题和特称命题(1)全称量词和存在量词
(2)全称命题和特称命题
【典型题型讲解】
考点一：充分条件与必要条件的判断
【典例例题】
例1．（2022·广东·金山中学高三期末）“ SKIPIF 1 < 0 ”是“点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 外”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
【答案】B
【详解】将 SKIPIF 1 < 0 化为标准方程，得 SKIPIF 1 < 0
当点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 外时，有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
∴“ SKIPIF 1 < 0 ”是“点 SKIPIF 1 < 0 ”在圆 SKIPIF 1 < 0 外”的必要不充分条件.
故选：B.
【方法技巧与总结】
1.要明确题中题意，找出条件 SKIPIF 1 < 0 和结论 SKIPIF 1 < 0 .
2.充分必要条件在面对集合问题时，一定是小集合推出大集合，而大集合推不出小集合.
【变式训练】
1.已知m，n是两条不重合的直线， SKIPIF 1 < 0 是一个平面， SKIPIF 1 < 0 ，则“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的（ ）
A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
【答案】A
【详解】
由线面垂直的性质知，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 成立，即充分性成立；
根据线面垂直的定义， SKIPIF 1 < 0 必须垂直平面 SKIPIF 1 < 0 内的两条相交直线，才有 SKIPIF 1 < 0 ，即必要性不成立.
故选：A.
2.已知 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，“函数 SKIPIF 1 < 0 为增函数”是“函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】C
【详解】
函数 SKIPIF 1 < 0 为增函数,则 SKIPIF 1 < 0 ,此时 SKIPIF 1 < 0 ,故函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增;当 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增时, , SKIPIF 1 < 0 ,所以 SKIPIF 1 < 0 ,故 SKIPIF 1 < 0 为增函数.
故选:C
3.在等比数列 SKIPIF 1 < 0 中，已知 SKIPIF 1 < 0 ，则“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【详解】
∵公比 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
又∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
即“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分不必要条件．
故选：A．
考点二：充分条件与必要条件的应用
【典例例题】
例1.“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，
即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 恒成立，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，
故 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，
所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0
因为 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ，
所以“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立”的充分不必要条件.
故选：A
【方法技巧与总结】
1.集合中推出一定是小集合推大集合，注意包含关系.
2.在充分必要条件求解参数取值范围时，要注意端点是否能取到问题，容易出错.
【变式训练】
1.若 SKIPIF 1 < 0 是 SKIPIF 1 < 0 成立的一个充分不必要条件，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】
由题意可得 SKIPIF 1 < 0 ，而
SKIPIF 1 < 0
SKIPIF 1 < 0
则 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
故选：D
2.（多选）“关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的一个必要不充分条件是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】BD
由题意，关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立，
则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
对于选项A中，“ SKIPIF 1 < 0 ”是“关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的充要条件；
对于选项B 中，“ SKIPIF 1 < 0 ”是“关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的必要不充分条件；
对于选项C中，“ SKIPIF 1 < 0 ”是“关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”的充分不必要条件；
对于选项D中，“ SKIPIF 1 < 0 ”是“关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 对 SKIPIF 1 < 0 恒成立”必要不充分条件.
故选：BD.
3.已知集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．若“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分条件，则实数 SKIPIF 1 < 0 的取值范围为________．
【答案】 SKIPIF 1 < 0
【详解】
函数 SKIPIF 1 < 0 的对称轴为 SKIPIF 1 < 0 ，开口向上，
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递增，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .
所以 SKIPIF 1 < 0 .
SKIPIF 1 < 0 ，
由于“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 ”的充分条件，
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
考点三：全称量词命题与存在量词命题的真假
【典例例题】
例1.已知 SKIPIF 1 < 0 ，下列四个命题：① SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，② SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，③ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，④ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
其中是真命题的有（ ）
A．①③B．②④C．①②D．③④
【答案】C
【详解】
对于①，由 SKIPIF 1 < 0 得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，①正确；
对于②， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，②正确；
对于③，函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为减函数，而 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，③错误；
对于④，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，④错误，
所以所给命题中，真命题的是①②．
故选：C
【方法技巧与总结】
1.全称量词命题与存在量词命题的真假判断既要通过汉字意思，又要通过数学结论.
2.全称量词命题和存在量词命题的真假性判断较为简单，注意细节即可.
【变式训练】
1．已知命题 SKIPIF 1 < 0 ：存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，命题 SKIPIF 1 < 0 ：对任意的 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 SKIPIF 1 < 0 ，命题 SKIPIF 1 < 0 ：存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，其中正确命题的个数是（ ）
A．0B．1C．2D．3
【答案】B
【详解】
当 SKIPIF 1 < 0 时，显然 SKIPIF 1 < 0 成立；当 SKIPIF 1 < 0 时，可知 SKIPIF 1 < 0 不成立；由辅助角得 SKIPIF 1 < 0 ，所以所以 SKIPIF 1 < 0 的最大值为5，所以 SKIPIF 1 < 0 为假.
故选：B
2．已知函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的定义域均为 SKIPIF 1 < 0 ，记 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ，则使得“ SKIPIF 1 < 0 ”成立的充要条件为（ ）
A． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 B． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0
C． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 D． SKIPIF 1 < 0 ， SKIPIF 1 < 0
【答案】C
【详解】
解：A选项表述的是 SKIPIF 1 < 0 的最小值大于 SKIPIF 1 < 0 的最大值；
B选项表述的是 SKIPIF 1 < 0 的最小值大于 SKIPIF 1 < 0 的最小值；
C选项表述的是 SKIPIF 1 < 0 的最大值大于 SKIPIF 1 < 0 的最大值成立的充要条件；
D选项是 SKIPIF 1 < 0 成立的充分不必要条件．
故选：C
3．下列命题中，真命题为（ ）
A．存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0
B．直线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 ，则平面 SKIPIF 1 < 0
C． SKIPIF 1 < 0 最小值为4
D． SKIPIF 1 < 0 ， SKIPIF 1 < 0 是 SKIPIF 1 < 0 成立的充分不必要条件
【答案】D
【详解】
对于A中，由指数函数 SKIPIF 1 < 0 的性质，可得 SKIPIF 1 < 0 恒成立，
所以不存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，所以A为假命题；
对于B中，如图所示，在正方体 SKIPIF 1 < 0 中，
设平面 SKIPIF 1 < 0 为平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 为平面 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 为直线 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 为直线 SKIPIF 1 < 0 ，
此时满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ，平面 SKIPIF 1 < 0 ，但平面 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 不垂直，
所以C为假命题.
对于C中，由 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 时，即 SKIPIF 1 < 0 时，等号成立，
显然 SKIPIF 1 < 0 不成立，所以C为假命题
对于D中，由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，即充分性成立；
反之：例如： SKIPIF 1 < 0 ，此时满足 SKIPIF 1 < 0 ，但 SKIPIF 1 < 0 不成立，即必要性不成立，
所以 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的充分不必要条件，所以D为真命题.
故选：D
4.（多选题）下列命题中的真命题是（ ）
A．∀x∈R，2x－1>0B．∀x∈N*，(x－1)2>0
C．∃x∈R，lgx