

新高考数学二轮复习考点突破讲义 第1部分 专题突破 专题4 第4讲 空间向量与距离、探究性问题(含解析)
展开
这是一份新高考数学二轮复习考点突破讲义 第1部分 专题突破 专题4 第4讲 空间向量与距离、探究性问题(含解析),共15页。
考点一 空间距离
核心提炼
(1)点到直线的距离
直线l的单位方向向量为u,A是直线l上的任一点,P为直线l外一点,设eq \(AP,\s\up6(→))=a,则点P到直线l的距离d=eq \r(a2-a·u2).
(2)点到平面的距离
平面α的法向量为n,A是平面α内任一点,P为平面α外一点,则点P到平面α的距离为d=eq \f(|\(AP,\s\up6(→))·n|,|n|).
考向1 点到直线的距离
例1 (1)(2022·广州模拟)如图,在四棱锥P-ABCD中,PB⊥平面ABCD,AB⊥BC,PB=AB=2BC=2,则点C到直线PA的距离为( )
A.eq \r(3) B.eq \r(5)
C.eq \r(2) D.2
答案 A
解析 因为PB⊥平面ABCD,AB⊂平面ABCD,BC⊂平面ABCD,
所以PB⊥AB,PB⊥BC,
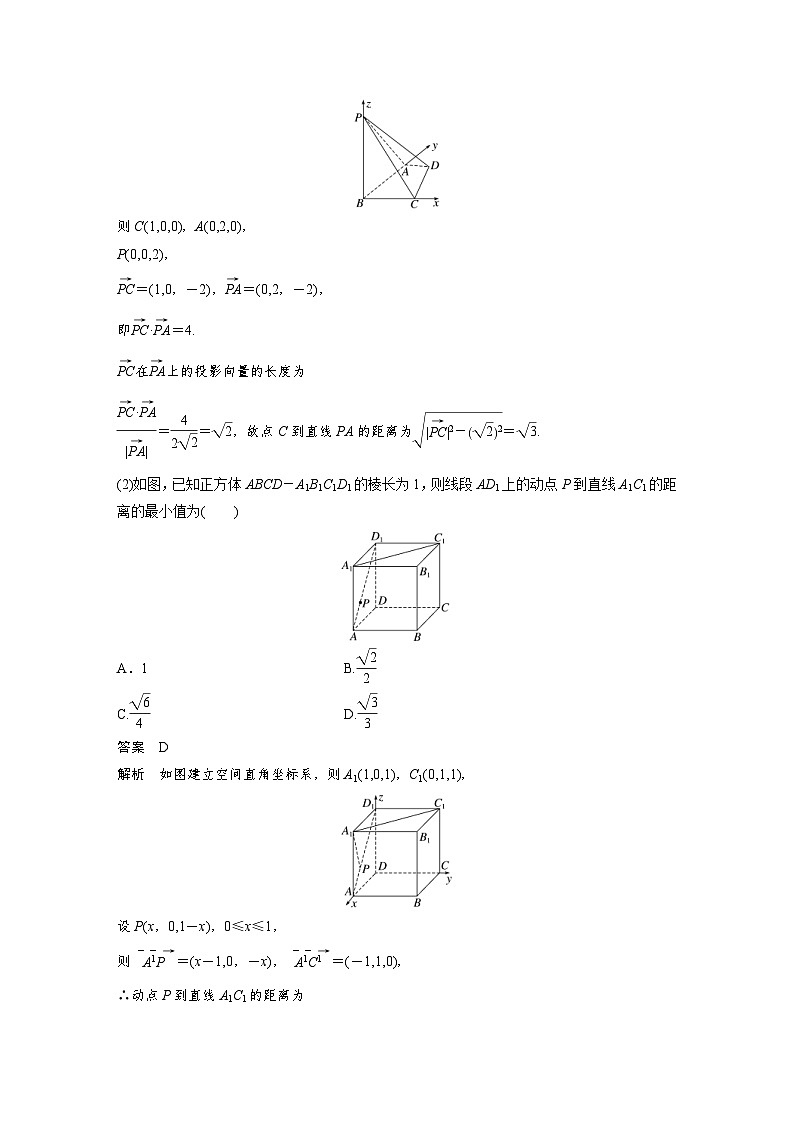
如图,以B为坐标原点,建立空间直角坐标系,
则C(1,0,0),A(0,2,0),
P(0,0,2),
eq \(PC,\s\up6(→))=(1,0,-2),eq \(PA,\s\up6(→))=(0,2,-2),
即eq \(PC,\s\up6(→))·eq \(PA,\s\up6(→))=4.
eq \(PC,\s\up6(→))在eq \(PA,\s\up6(→))上的投影向量的长度为
eq \f(\(PC,\s\up6(→))·\(PA,\s\up6(→)),|\(PA,\s\up6(→))|)=eq \f(4,2\r(2))=eq \r(2),故点C到直线PA的距离为eq \r(|\(PC,\s\up6(→))|2-\r(2)2)=eq \r(3).
(2)如图,已知正方体ABCD-A1B1C1D1的棱长为1,则线段AD1上的动点P到直线A1C1的距离的最小值为( )
A.1 B.eq \f(\r(2),2)
C.eq \f(\r(6),4) D.eq \f(\r(3),3)
答案 D
解析 如图建立空间直角坐标系,则A1(1,0,1),C1(0,1,1),
设P(x,0,1-x),0≤x≤1,
则eq \(A1P,\s\up6(--→))=(x-1,0,-x),eq \(A1C1,\s\up6(--→))=(-1,1,0),
∴动点P到直线A1C1的距离为
d=eq \r(|\(A1P,\s\up6(--→))|2-\b\lc\|\rc\|(\a\vs4\al\c1(\f(\(A1P,\s\up6(--→))·\(A1C1,\s\up6(--→)),|\(A1C1,\s\up6(--→))|)))2)
=eq \r(x-12+-x2-\b\lc\(\rc\)(\a\vs4\al\c1(\f(1-x,\r(2))))2)
=eq \r(\f(3,2)x2-x+\f(1,2))=eq \r(\f(3,2)\b\lc\(\rc\)(\a\vs4\al\c1(x-\f(1,3)))2+\f(1,3))≥eq \f(\r(3),3),
当且仅当x=eq \f(1,3)时取等号,即线段AD1上的动点P到直线A1C1的距离的最小值为eq \f(\r(3),3).
考向2 点到平面的距离
例2 (1)(2022·湖北联考)在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=PC=1,PB=PD=eq \r(2),点E为线段PD上一点,且PE=2ED,则点P到平面ACE的距离为______.
答案 eq \f(\r(78),13)
解析 如图,连接AC,BD交于点O,连接OP,以OB,OC,OP所在直线分别为x,y,z轴,建立空间直角坐标系,
设AB=2a,则OA=a,OB=eq \r(3)a,
因为PA2-OA2=PB2-OB2,
所以1-a2=2-3a2,
解得a=eq \f(\r(2),2),则OP=eq \f(\r(2),2),
所以Aeq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(\r(2),2),0)),Ceq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(\r(2),2),0)),
Peq \b\lc\(\rc\)(\a\vs4\al\c1(0,0,\f(\r(2),2))),Deq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(6),2),0,0)),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(6),3),0,\f(\r(2),6))),
则eq \(AC,\s\up6(→))=(0,eq \r(2),0),
eq \(AE,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(\r(6),3),\f(\r(2),2),\f(\r(2),6))),
eq \(AP,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(\r(2),2),\f(\r(2),2))),
设平面ACE的一个法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(AC,\s\up6(→))=\r(2)y=0,,n·\(AE,\s\up6(→))=-\f(\r(6),3)x+\f(\r(2),2)y+\f(\r(2),6)z=0,))
取x=1,得n=(1,0,2eq \r(3)),
所以点P到平面ACE的距离
d=eq \f(|n·\(AP,\s\up6(→))|,|n|)=eq \f(\r(6),\r(13))=eq \f(\r(78),13).
(2)(2022·沈阳模拟)如图,若正四棱柱ABCD-A1B1C1D1的底边长为2,∠B1AB=eq \f(π,3),E是D1D的中点,则A1C1到平面EAC的距离为________.
答案 eq \f(2\r(30),5)
解析 由棱柱的几何性质可知,A1C1∥AC,
又A1C1⊄平面EAC,AC⊂平面EAC,
所以A1C1∥平面EAC,
所以点A1到平面EAC的距离即为直线A1C1到平面EAC的距离,
因为正四棱柱ABCD-A1B1C1D1的底边长为2,∠B1AB=eq \f(π,3),则AA1=2eq \r(3),
以点A为坐标原点建立空间直角坐标系,如图所示,
则A(0,0,0),A1(0,0,2eq \r(3)),C(2,2,0),E(0,2,eq \r(3)),
所以eq \(AC,\s\up6(→))=(2,2,0),
eq \(AE,\s\up6(→))=(0,2,eq \r(3)),
eq \(AA1,\s\up6(--→))=(0,0,2eq \r(3)),
设平面EAC的一个法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(AC,\s\up6(→))=0,,n·\(AE,\s\up6(→))=0,))
即eq \b\lc\{\rc\ (\a\vs4\al\c1(2x+2y=0,,2y+\r(3)z=0,))
令x=eq \r(3),得y=-eq \r(3),z=2,
故n=(eq \r(3),-eq \r(3),2),
所以点A1到平面EAC的距离
d=eq \f(|\(AA1,\s\up6(--→))·n|,|n|)=eq \f(4\r(3),\r(3+3+4))=eq \f(2\r(30),5),
故A1C1到平面EAC的距离为eq \f(2\r(30),5).
规律方法 (1)求直线到平面的距离的前提是直线与平面平行.求直线到平面的距离可转化成直线上任一点到平面的距离.
(2)求点到平面的距离有两种方法,一是利用空间向量点到平面的距离公式,二是利用等体积法.
跟踪演练1 (1)(2022·邢台联考)PA,PB,PC是从点P出发的三条线段,每两条线段的夹角均为60°,PA=PB=PC=1,若M满足eq \(PM,\s\up6(→))=eq \(PA,\s\up6(→))+2eq \(PB,\s\up6(→))+3eq \(PC,\s\up6(→)),则点M到直线AB的距离为( )
A.eq \r(3) B.3
C.2eq \r(3) D.3eq \r(2)
答案 D
解析 eq \(AM,\s\up6(→))=eq \(PM,\s\up6(→))-eq \(PA,\s\up6(→))=2eq \(PB,\s\up6(→))+3eq \(PC,\s\up6(→)),
则|eq \(AM,\s\up6(→))|=eq \r(\(\s\up7(),\s\d5())2\(PB,\s\up6(→))+3\(PC,\s\up6(→))2)
=eq \r(\(\s\up7(),\s\d5())4\(PB,\s\up6(→))2+12\(PB,\s\up6(→))·\(PC,\s\up6(→))+9\(PC,\s\up6(→))2)
=eq \r(4+12×1×1×\f(1,2)+9)=eq \r(19),
则eq \(AM,\s\up6(→))·eq \(AB,\s\up6(→))=(2eq \(PB,\s\up6(→))+3eq \(PC,\s\up6(→)))·(eq \(PB,\s\up6(→))-eq \(PA,\s\up6(→)))
=2eq \(PB,\s\up6(→))2-2eq \(PB,\s\up6(→))·eq \(PA,\s\up6(→))+3eq \(PC,\s\up6(→))·eq \(PB,\s\up6(→))-3eq \(PC,\s\up6(→))·eq \(PA,\s\up6(→))
=2-2×1×1×eq \f(1,2)+3×1×1×eq \f(1,2)-3×1×1×eq \f(1,2)=1,
|eq \(AB,\s\up6(→))|=eq \r(\(PB,\s\up6(→))-\(PA,\s\up6(→))2)=eq \r(\(PB,\s\up6(→))2-2\(PB,\s\up6(→))·\(PA,\s\up6(→))+\(PA,\s\up6(→))2)
=eq \r(1-2×1×1×\f(1,2)+1)=1,
则点M到直线AB的距离
d=eq \r(|\(AM,\s\up6(→))|2-\b\lc\(\rc\)(\a\vs4\al\c1(\f(|\(AM,\s\up6(→))·\(AB,\s\up6(→))|,|\(AB,\s\up6(→))|)))2)=3eq \r(2).
(2)(2022·茂名模拟)如图,正方体ABCD-A1B1C1D1的棱长为1,中心为O,eq \(BF,\s\up6(→))=eq \f(1,2)eq \(BC,\s\up6(→)),eq \(A1E,\s\up6(--→))=eq \f(1,4)eq \(A1A,\s\up6(--→)),则四面体OEBF的体积为( )
A.eq \f(1,12) B.eq \f(1,24) C.eq \f(1,48) D.eq \f(1,96)
答案 D
解析 如图,以D为坐标原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,
则Oeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),\f(1,2),\f(1,2))),B(1,1,0),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(1,0,\f(3,4))),Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1,0)),
eq \(OE,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),-\f(1,2),\f(1,4))),eq \(OB,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),\f(1,2),-\f(1,2))),
eq \(BE,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-1,\f(3,4))),
则|eq \(OE,\s\up6(→))|=eq \f(3,4),|eq \(OB,\s\up6(→))|=eq \f(\r(3),2),eq \b\lc\|\rc\|(\a\vs4\al\c1(\(BE,\s\up6(→))))=eq \f(5,4),
∴cs∠BOE=eq \f(\(OB,\s\up6(→))·\(OE,\s\up6(→)),|\(OB,\s\up6(→))||\(OE,\s\up6(→))|)
=eq \f(\f(1,2)×\f(1,2)+\f(1,2)×\b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2)))-\f(1,2)×\f(1,4),\f(\r(3),2)×\f(3,4))=-eq \f(\r(3),9).
∴∠BOE∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2),π)),则sin∠BOE=eq \f(\r(78),9).
∴S△OEB=eq \f(1,2)OB·OE·sin∠BOE=eq \f(\r(26),16).
设平面OEB的一个法向量为n=(x,y,z),
由eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(OE,\s\up6(→))=\f(1,2)x-\f(1,2)y+\f(1,4)z=0,,n·\(OB,\s\up6(→))=\f(1,2)x+\f(1,2)y-\f(1,2)z=0,))取z=1,
得n=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4),\f(3,4),1)),又eq \(BF,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(-\f(1,2),0,0)),
∴F到平面OEB的距离h=eq \f(|n·\(BF,\s\up6(→))|,|n|)=eq \f(\r(26),52),
∴四面体OEBF的体积V=eq \f(1,3)×eq \f(\r(26),16)×eq \f(\r(26),52)=eq \f(1,96).
考点二 空间中的探究性问题
核心提炼
与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或两平面的夹角满足特定要求时的存在性问题.处理原则:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.
例3 (2022·汕头模拟)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD,△ABC是底面的内接正三角形,且DO=6,P是线段DO上一点.
(1)是否存在点P,使得PA⊥平面PBC,若存在,求出PO的值;若不存在,请说明理由;
(2)当PO为何值时,直线EP与平面PBC所成的角的正弦值最大.
解 (1)存在,由题意得AO=eq \f(1,2)AE=eq \f(1,2)AD,
因为AD2=DO2+AO2,
所以AD2=36+eq \f(1,4)AD2,
所以AD=4eq \r(3),AO=2eq \r(3),
因为△ABC是底面圆的内接正三角形,
所以eq \f(AB,sin 60°)=2×2eq \r(3),
所以AB=6,
又由题意得PA2=12+PO2,
假设PA⊥平面PBC,则PA⊥PB,
所以AB2=PA2+PB2,
所以36=12+PO2+12+PO2,所以PO=eq \r(6),
此时PA⊥PC,PA⊥PB,PB∩PC=P,
PB,PC⊂平面PBC,
所以当PO=eq \r(6)时,PA⊥平面PBC.
(2)如图所示,建立以点O为坐标原点的空间直角坐标系.
设PO=x,0≤x≤6,
所以P(0,0,x),E(-eq \r(3),3,0),B(eq \r(3),3,0),
C(-2eq \r(3),0,0),
所以eq \(EP,\s\up6(→))=(eq \r(3),-3,x),eq \(PB,\s\up6(→))=(eq \r(3),3,-x),
eq \(PC,\s\up6(→))=(-2eq \r(3),0,-x),
设平面PBC的法向量为n=(a,b,c),
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(PB,\s\up6(→))=\r(3)a+3b-cx=0,,n·\(PC,\s\up6(→))=-2\r(3)a-cx=0,))
所以n=(x,-eq \r(3)x,-2eq \r(3)).
设直线EP与平面PBC所成的角为θ,
由题意得sin θ=eq \f(|\r(3)x+3\r(3)x-2\r(3)x|,\r(3+9+x2)·\r(x2+3x2+12))=eq \f(2\r(3)x,\r(12+x2)·\r(4x2+12))=eq \f(\r(3),\r(x2+\f(36,x2)+15))≤eq \f(1,3).
当且仅当PO=x=eq \r(6)时等号成立,此时直线EP与平面PBC所成的角的正弦值最大.
规律方法 解决立体几何中探索性问题的基本方法
(1)通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明,否则假设不成立.
(2)探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.
跟踪演练2 (2022·武汉质检)如图,在四棱锥P-ABCD中,四边形ABCD为平行四边形,PA=PD=eq \r(2),AB=1,AD=2,PD⊥AB.
(1)证明:平面PCD⊥平面PAB;
(2)若PB=eq \r(3),试在棱PD上确定一点E,使得平面PAB与平面EAC的夹角的余弦值为eq \f(2\r(7),7).
(1)证明 因为PA=PD=eq \r(2),AD=2,
所以PA2+PD2=AD2,所以PD⊥PA,
又因为PD⊥AB,AB,PA⊂平面PAB,
且AB∩PA=A,
所以PD⊥平面PAB,
又因为PD⊂平面PCD,
所以平面PCD⊥平面PAB.
(2)解 因为PA=eq \r(2),AB=1,PB=eq \r(3),
所以PA2+AB2=PB2,所以AB⊥PA,
又因为PD⊥AB,PA,PD⊂平面PAD,
且PD∩PA=A,
所以AB⊥平面PAD,
因为AD⊂平面PAD,
所以AB⊥AD,
所以四边形ABCD为矩形.
以A为原点,eq \(AB,\s\up6(→)),eq \(AD,\s\up6(→))分别为x轴、y轴的正方向,建立空间直角坐标系,如图所示,
则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,1,1),
所以eq \(AC,\s\up6(→))=(1,2,0),eq \(AP,\s\up6(→))=(0,1,1),eq \(PD,\s\up6(→))=(0,1,-1),
由PD⊥平面PAB,可得向量eq \(PD,\s\up6(→))=(0,1,-1)是平面PAB的一个法向量.
设eq \(ED,\s\up6(→))=λeq \(PD,\s\up6(→)),0≤λ≤1,
则E(0,2-λ,λ),
所以eq \(AE,\s\up6(→))=(0,2-λ,λ).
设平面EAC的一个法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(AE,\s\up6(→))=0,,n·\(AC,\s\up6(→))=0,))所以eq \b\lc\{\rc\ (\a\vs4\al\c1(2-λy+λz=0,,x+2y=0,))
令y=-1,可得x=2,z=eq \f(2-λ,λ),
所以n=eq \b\lc\(\rc\)(\a\vs4\al\c1(2,-1,\f(2-λ,λ))),
所以|cs〈eq \(PD,\s\up6(→)),n〉|=eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(\(PD,\s\up6(→))·n,|\(PD,\s\up6(→))||n|)))=eq \f(2\r(7),7),
可得12λ2-8λ+1=0,
解得λ=eq \f(1,2)或λ=eq \f(1,6),
即当点E满足eq \(ED,\s\up6(→))=eq \f(1,2)eq \(PD,\s\up6(→))或eq \(ED,\s\up6(→))=eq \f(1,6)eq \(PD,\s\up6(→))时,平面PAB与平面EAC的夹角的余弦值为eq \f(2\r(7),7).
专题强化练
1.(2022·山东联考)如图,在正四棱柱ABCD-A1B1C1D1中,AB=1,E为CC1的中点.
(1)当AA1=2时,证明:平面BDE⊥平面A1B1E.
(2)当AA1=3时,求A1到平面BDE的距离.
(1)证明 当AA1=2时,B1E=eq \r(2),BE=eq \r(2),
所以B1E2+BE2=BBeq \\al(2,1),所以B1E⊥BE.
又A1B1⊥平面BCC1B1,则A1B1⊥BE.
因为A1B1∩B1E=B1,A1B1,B1E⊂平面A1B1E,
所以BE⊥平面A1B1E,
又BE⊂平面BDE,
所以平面BDE⊥平面A1B1E.
(2)解 以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),B(1,1,0),
A1(1,0,3),Eeq \b\lc\(\rc\)(\a\vs4\al\c1(0,1,\f(3,2))).
所以eq \(DB,\s\up6(→))=(1,1,0),eq \(DE,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(0,1,\f(3,2))),eq \(DA1,\s\up6(--→))=(1,0,3).
设平面BDE的一个法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(DB,\s\up6(→))=0,,n·\(DE,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(x+y=0,,y+\f(3,2)z=0,))
不妨令z=2,则y=-3,x=3,
得n=(3,-3,2).故A1到平面BDE的距离
d=eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(n·\(DA1,\s\up6(--→)),\b\lc\|\rc\|(\a\vs4\al\c1(n)))))=eq \f(9,\r(22))=eq \f(9\r(22),22).
2.(2022·聊城质检)如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2AB=2,E,F分别为棱AA1,CC1的中点,G为棱DD1上的动点.
(1)求证:B,E,D1,F四点共面;
(2)是否存在点G,使得平面GEF⊥平面BEF?若存在,求出DG的长度;若不存在,说明理由.
(1)证明 如图所示,连接D1E,D1F,取BB1的中点为M,连接MC1,ME,
因为E为AA1的中点,
所以EM∥A1B1∥C1D1,
且EM=A1B1=C1D1,
所以四边形EMC1D1为平行四边形,所以D1E∥MC1,
又因为F为CC1的中点,
所以BM∥C1F,且BM=C1F,
所以四边形BMC1F为平行四边形,
所以BF∥MC1,所以BF∥D1E,
所以B,E,D1,F四点共面.
(2)解 以D为坐标原点,DA,DC,DD1分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,
假设存在满足题意的点G(0,0,t)(0≤t≤2),
由已知B(1,1,0),E(1,0,1),F(0,1,1),
则eq \(EF,\s\up6(→))=(-1,1,0),eq \(EB,\s\up6(→))=(0,1,-1),
eq \(EG,\s\up6(→))=(-1,0,t-1),
设平面BEF的一个法向量为n1=(x1,y1,z1),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n1·\(EF,\s\up6(→))=0,,n1·\(EB,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(-x1+y1=0,,y1-z1=0,))
取x1=1,则n1=(1,1,1);
设平面GEF的一个法向量为n2=(x2,y2,z2),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n2·\(EF,\s\up6(→))=0,,n2·\(EG,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(-x2+y2=0,,-x2+t-1z2=0,))
取x2=t-1,则n2=(t-1,t-1,1).
因为平面GEF⊥平面BEF,
所以n1·n2=0,
即t-1+t-1+1=0,解得t=eq \f(1,2).
所以存在满足题意的点G,使得平面GEF⊥平面BEF,DG的长度为eq \f(1,2).
3.(2022·湖北七市联考)如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,PA=AB,E,F分别为线段PB,BC上的动点.
(1)若E为线段PB的中点,证明:平面AEF⊥平面PBC;
(2)若BE=eq \r(2)BF,且平面AEF与平面PBC夹角的余弦值为eq \f(\r(7),14),试确定点F的位置.
(1)证明 由PA⊥底面ABCD,可得PA⊥BC,
又在正方形ABCD中,BC⊥AB,
且PA∩AB=A,PA,AB⊂平面PAB,
则BC⊥平面PAB,
又AE⊂平面PAB,
所以BC⊥AE.
由PA=AB,E为PB中点,可得AE⊥PB,
又PB∩BC=B,PB,BC⊂平面PBC,
则AE⊥平面PBC,又AE⊂平面AEF,从而平面AEF⊥平面PBC.
(2)解 以A为坐标原点,AB,AD,AP分别为x,y,z轴,建立如图所示的空间直角坐标系.设AB=1,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),P(0,0,1).
由(1)可知n1=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),0,\f(1,2)))为平面PBC的一个法向量.
由BE=eq \r(2)BF,可知EF∥PC,
设eq \(BF,\s\up6(→))=λeq \(BC,\s\up6(→)),eq \(BE,\s\up6(→))=λeq \(BP,\s\up6(→)),
则eq \(BF,\s\up6(→))=(0,λ,0),eq \(BE,\s\up6(→))=(-λ,0,λ),
可得eq \(AF,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(BF,\s\up6(→))=(1,λ,0),
eq \(AE,\s\up6(→))=eq \(AB,\s\up6(→))+eq \(BE,\s\up6(→))=(1-λ,0,λ).
设平面AEF的一个法向量为n2=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n2·\(AF,\s\up6(→))=0,,n2·\(AE,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(x+λy=0,,1-λx+λz=0,))
取y=1,则x=-λ,z=1-λ,
即n2=(-λ,1,1-λ).
从而,由eq \b\lc\|\rc\|(\a\vs4\al\c1(cs〈n1,n2〉))=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(n1·n2)),\b\lc\|\rc\|(\a\vs4\al\c1(n1))\b\lc\|\rc\|(\a\vs4\al\c1(n2)))
=eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(1-2λ)),\r(2)·\r(2λ2-2λ+2))=eq \f(\r(7),14),
解得λ=eq \f(1,3)或λ=eq \f(2,3),即F在BC的三等分点处.
4.(2022·长沙十六校联考)如图,在四棱锥P-ABCD中,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,AB⊥AD,AD=2AB=2BC=2,PC=eq \r(2),E为PD的中点.
(1)求直线PB与平面PAC所成角的正弦值;
(2)设F是BE的中点,判断点F是否在平面PAC内,并证明结论.
解 (1)在直角梯形ABCD中,
由已知可得AC=eq \r(2),CD=eq \r(2),
∴AC2+CD2=AD2,∴AC⊥CD,
又△ADP是以AD为斜边的等腰直角三角形,
∴PA=PD=eq \r(2),
如图,取AD的中点O,连接OC,OP,
则OC=OA=OD=1,OP=1,
则△OAP≌△OCP≌△ODP,
∴∠POA=∠POC=∠POD=90°,
∴OP⊥AD,OP⊥OC,
而OC∩AD=O,OC,AD⊂平面ABCD,
∴OP⊥平面ABCD,
因此以AB,AD为x轴、y轴,过点A作平行于OP的直线为z轴建立空间直角坐标系,如图,
则A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),
P(0,1,1),eq \(AP,\s\up6(→))=(0,1,1),eq \(AC,\s\up6(→))=(1,1,0),
设平面PAC的一个法向量为n=(x,y,z),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(AP,\s\up6(→))=0,,n·\(AC,\s\up6(→))=0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(y+z=0,,x+y=0,))
取y=-1,则x=z=1,即n=(1,-1,1),
又eq \(BP,\s\up6(→))=(-1,1,1),
设直线PB与平面PAC所成角为θ,
∴sin θ=|cs〈eq \(BP,\s\up6(→)),n〉|
=eq \f(|\(BP,\s\up6(→))·n|,|\(BP,\s\up6(→))||n|)=eq \f(|-1-1+1|,\r(3)×\r(3))=eq \f(1,3),
∴直线PB与平面PAC所成角的正弦值为eq \f(1,3).
(2)点F在平面PAC内,证明如下:
由(1)可得Eeq \b\lc\(\rc\)(\a\vs4\al\c1(0,\f(3,2),\f(1,2))),Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),\f(3,4),\f(1,4))),
eq \(AF,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),\f(3,4),\f(1,4))),设eq \(AF,\s\up6(→))=xeq \(AC,\s\up6(→))+yeq \(AP,\s\up6(→)),
则eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),\f(3,4),\f(1,4)))=x(1,1,0)+y(0,1,1),
则eq \b\lc\{\rc\ (\a\vs4\al\c1(x=\f(1,2),,x+y=\f(3,4),,y=\f(1,4),))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(x=\f(1,2),,y=\f(1,4),))
∴eq \(AF,\s\up6(→))=eq \f(1,2)eq \(AC,\s\up6(→))+eq \f(1,4)eq \(AP,\s\up6(→)),∴eq \(AF,\s\up6(→))与eq \(AC,\s\up6(→)),eq \(AP,\s\up6(→))共面,
∴F在平面PAC内.
相关试卷
这是一份新高考数学二轮复习考点突破讲义 第1部分 专题突破 专题6 第4讲 母题突破4 探索性问题(含解析),共8页。
这是一份新高考数学二轮复习考点突破讲义 第1部分 专题突破 专题6 第4讲 母题突破3 定值问题(含解析),共8页。
这是一份新高考数学二轮复习考点突破讲义 第1部分 专题突破 专题6 第4讲 母题突破2 定点问题(含解析),共7页。









