苏科版九年级上册3.4 方差学案

这是一份苏科版九年级上册3.4 方差学案，共4页。学案主要包含了学习目标等内容，欢迎下载使用。

【学习目标】:二次备课
1.经历刻画数据离散程度的过程，了解极差、方差是刻画数据离散程度的统计量，并在具体情境中加以应用；
2.掌握极差、方差的概念，会计算极差、方差，理解它们的统计意义.
【重难点】:方差的计算
一、情境创设
乒乓球的标准直径为40mm。质检部门抽取了A厂生产的10只乒乓球，对其直径进行检测，结果如下（单位：mm）：
A厂：40.0，39.9，40.0，40.1，40.2， 39.8，40.0，39.9，40.0，40.1；
上述数据的变化范围是多少？
上述数据中 “A厂中”最大值为 ，最小值为 。
最大值与最小值的差为 我们把这样的差叫做极差。
极差＝ 最大值-最小值
极差反映了一组数据的变化范围，在一定程度上描述了这组数据的离散程度。
新知探究
质检部门又抽取了B厂生产的10只乒乓球，对其直径进行检测，结果如下（单位：mm）：
40.0 ， 40.2 ， 39.8 ， 40.1 ， 39.9 ，
40.1 ， 39.9 ， 40.2 ， 39.8 ， 40.0
问：1、这组数据的极差是多少？
2、怎样比较这两组数据的离散程度呢？
用一组数据、、…、与它们的平均数的差的平方的平均数，即s2=1n[（x1−x）2+（x2−x）2+…+（xn−x）2]来描述这组数据的离散程度，并把它叫做这组数据的方差.
一组数据的方差越大，说明这组数据的离散程度越 ；
一组数据的方差越小，说明这组数据的离散程度越 .
三、新知巩固
1．（2021秋•徐州期末）抽查甲、乙两种消毒用品的净含量，若其方差分别为S甲2＝1.5ml2，S乙2＝1.1ml2，则净含量较为稳定的是 ．（填“甲”或“乙”）
2.一组数据的方差计算公式为：s2=14[(6−x)2+(6−x)2+(7−x)2+(9−x)2]，下列关于这组数据的说法错误的是（ ）
A．平均数是7 B．中位数是6.5 C．众数是6 D．方差是1
3.将数据a、b、e、d、e、f的每一个数据都增加5，则下列说法中错误的是（ ）
A．平均数增加5 B．中位数增加5C．有众数则增加5 D．方差增加5
例题讲评
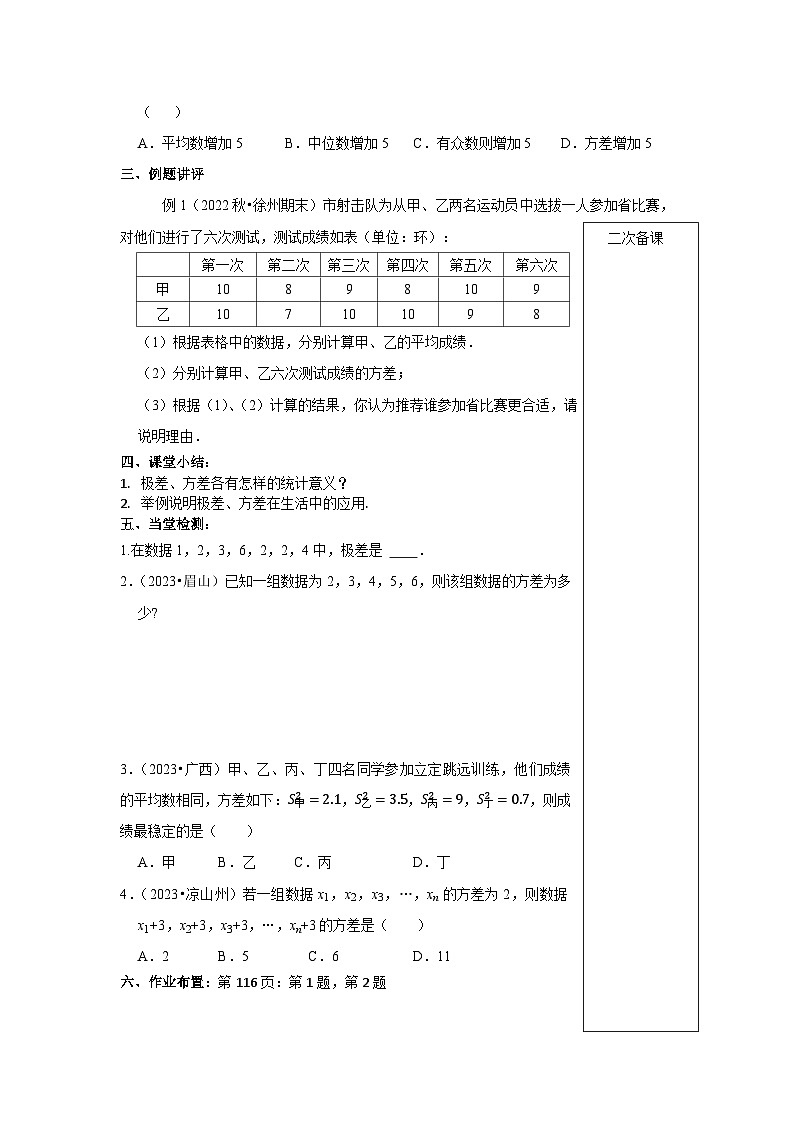
例1（2022秋•徐州期末）市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如表（单位：环）：二次备课
（1）根据表格中的数据，分别计算甲、乙的平均成绩．
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由．
四、课堂小结：
极差、方差各有怎样的统计意义？
举例说明极差、方差在生活中的应用.
五、当堂检测：
1.在数据1，2，3，6，2，2，4中，极差是 ．
2．（2023•眉山）已知一组数据为2，3，4，5，6，则该组数据的方差为多少?
3．（2023•广西）甲、乙、丙、丁四名同学参加立定跳远训练，他们成绩的平均数相同，方差如下：S甲2=2.1，S乙2=3.5，S丙2=9，S丁2=0.7，则成绩最稳定的是（ ）
A．甲 B．乙 C．丙D．丁
4．（2023•凉山州）若一组数据x1，x2，x3，…，xn的方差为2，则数据x1+3，x2+3，x3+3，…，xn+3的方差是（ ）
A．2 B．5 C．6D．11
六、作业布置：第116页：第1题，第2题
教学反思：
六、作业布置：第87页：第1题，第3题
教学反思：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8