


还剩27页未读,
继续阅读
2023八年级数学上册第12章整式的乘除本章归纳总结课件(华东师大版)
展开
这是一份2023八年级数学上册第12章整式的乘除本章归纳总结课件(华东师大版),共35页。
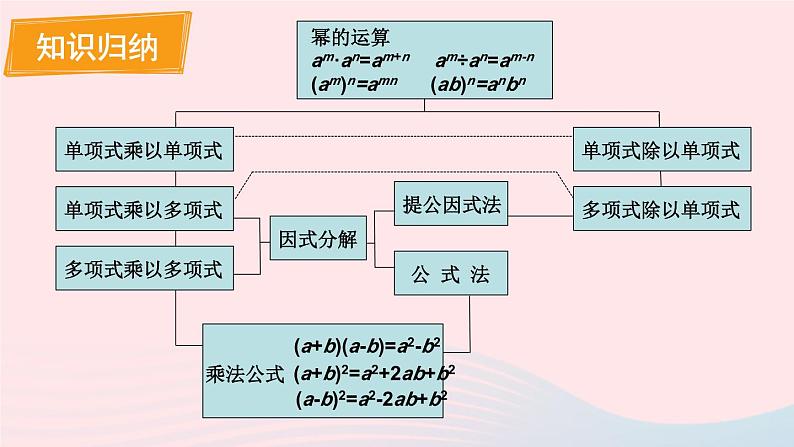
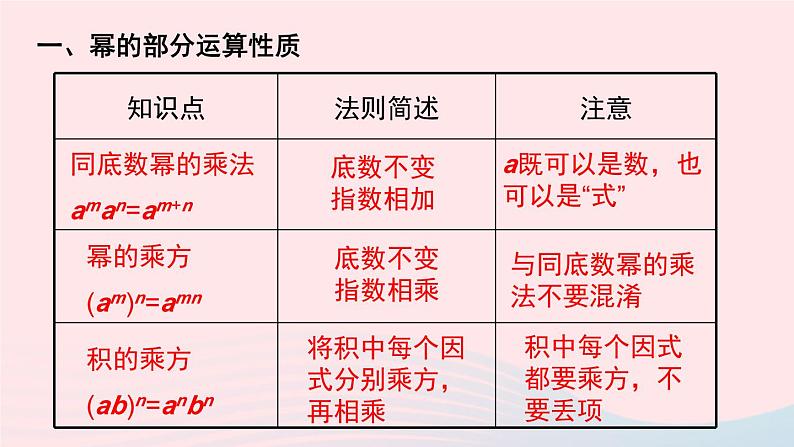
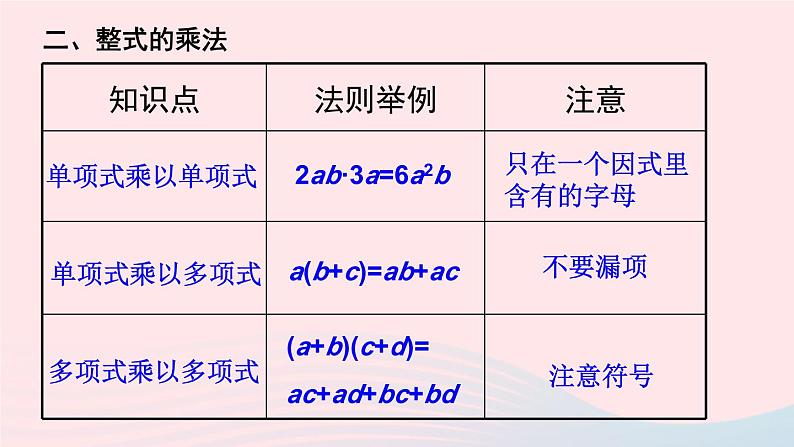
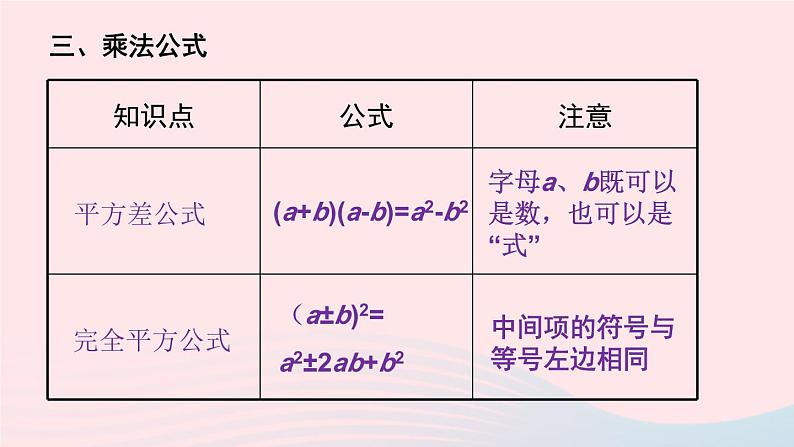
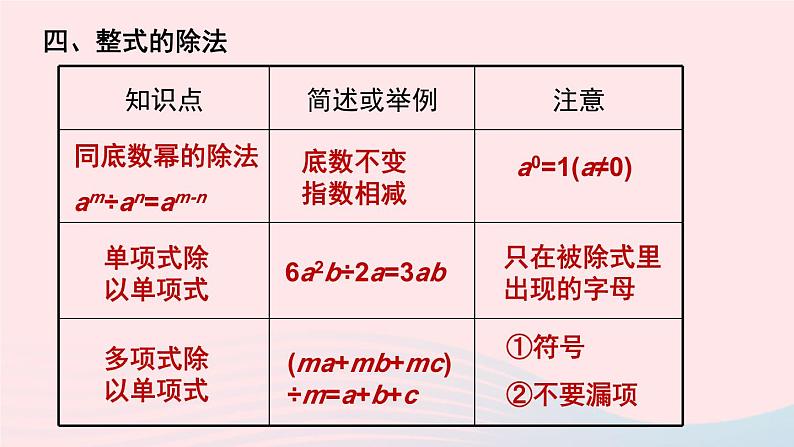
章末复习华东师大版 八年级数学上册同底数幂的乘法aman=am+n幂的乘方(am)n=amn积的乘方(ab)n=anbn底数不变指数相加a既可以是数,也可以是“式”底数不变指数相乘与同底数幂的乘法不要混淆将积中每个因式分别乘方,再相乘 积中每个因式都要乘方,不要丢项一、幂的部分运算性质单项式乘以单项式单项式乘以多项式多项式乘以多项式2ab·3a=6a2b只在一个因式里含有的字母a(b+c)=ab+ac不要漏项(a+b)(c+d)=ac+ad+bc+bd注意符号二、整式的乘法三、乘法公式平方差公式完全平方公式(a+b)(a-b)=a2-b2(a±b)2=a2±2ab+b2字母a、b既可以是数,也可以是“式”中间项的符号与等号左边相同同底数幂的除法am÷an=am-n单项式除以单项式多项式除以单项式底数不变指数相减a0=1(a≠0)6a2b÷2a=3ab只在被除式里出现的字母(ma+mb+mc) ÷m=a+b+c①符号②不要漏项四、整式的除法1.计算:(1)a10·a8(2)(xy)2·(xy)3(3)[(-x)3]2(4)[(-x)2]3(5)(-2mn2)3(6)(y3)2·(y2)4=a10+8=a18=(xy)2+3=(xy)5=x5y5=(-x)6=x6=(-x)6=x6=-8m3n6=y6·y8=y14A组2.计算:(1)2a·3a2(2)(-3xy)·(-4yz)(3)(-2a2)2·(-5a3)(4)(-3x)·(2x2-x-1)=2·3a·a2=6a3=(-3)×(-4)xy·yz=12xy2z=4a4·(-5a3)=4×(-5)a4·a3=-20a7=(-3x)·2x2-(-3x)x-(-3x)=-6x3+3x2+3x2.计算:(5)(x-2)(x-6)(6)(2x-1)(3x+2)(7)(y-2)(y2-6y-9)(8)(p-6q)(p2+pq+q2)=(x-2)x-6(x-2)=x2-2x-6x+12=x2-8x+12=2x(3x+2)-(3x+2)=6x2+4x-3x-2=6x2+x-2=y(y2-6y-9)-2(y2-6y-9)=y3-6y2-9y-2y2+12y+18=y3-8y2+3y+18=p(p2+pq+q2)-6q(p2+pq+q2)=p3+p2q+pq2-6p2q-6pq2-6q3=p3-5p2q-5pq2-6q33.计算:(1)(x+2)(x-2)(2)(m+n)(m-n)(3)(-m-n)(-m+n)(4)(-m-n)(m+n)=x2-4=m2-n2=-(m+n)(n-m)=-(n2-m2)=-n2+m2=-(m+n)(m+n)=-(m2+2mn+n2)=-m2-2mn-n2(5)(-m+n)(m-n)=-(m-n)(m-n)=-(m2-2mn+n2)=-m2+2mn-n24.计算:(1)20132-2014×2012(2)(4×104)×(2×103)-(6.5×103)×(6×103)=20132-(2013+1)×(2013-1)=20132-20132+1=1=8×104×103-39×103×103=8×107-3.9×107=4.1×1074.计算:(3)(2x+5)2-(2x-5)2=(2x+5-2x+5)(2x+5+2x-5)=10·4x=40x= -4x4.计算:(6)(-6x2)2+(-3x)3·x=2x2y+3xy-x2y=3xy+x2y=36x4-27x3·x=9x45.计算:(1)a·a4÷a3(2)(-x)6÷(-x)2·(-x)3(3)27x8÷3x4(4)-12m3n3÷4m2n3=a5÷a3=a2= (-x)6-2+3=-x7=9x8-4=9x4=-3m3-2n3-3=-3m5.计算:(5)(6x2y3z2)2÷4x3y4(6)(-6a2b5c)÷(-2ab2)2=36x4y6z4÷4x3y4=9x4-3y6-4z4=9xy2z4=(-6a2b5c)÷4a2b4=-1.5a2-2b5-4c=-1.5bc6.计算:(1)(6a4-4a3-2a2)÷(-2a2)(2)(4x3y+6x2y2-xy3)÷2xy=6a4÷(-2a2)-4a3÷(-2a2)-2a2÷(-2a2)=-3a2+2a+1=4x3y÷2xy+6x2y2÷2xy-xy3÷2xy=2x2+3xy-0.5y26.计算:(4)(2ab2-b3)2÷2b3=4x2+8x-2=(4a2b4-4ab5+b6)÷2b3=4a2b4÷2b3-4ab5÷2b3+b6÷2b3=2a2b-2ab2+0.5b37.计算:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x.解: [(x-2y)[(x-2y)+(x+2y)]-2x(2x-y)]÷2x.=[2x(x-2y)-2x(2x-y)]÷2x.=2x(x-2y-2x+y)÷2x.=-x-y8.把下列多项式分解因式:(1)x2-25x(2)2x2y2-4y3z(3)am-an+ap(4)x3-25x=x(x-25)=2y2(x2-2yz)=a(m-n+p)=x(x2-25)=x(x+5)(x-5)8.把下列多项式分解因式:(5)1-4x2(6)25x2+20xy+4y2(7)x3-4x2+4x=(1-2x)(1+2x)=(5x+2y)2=x(x2-4x+4)=x(x-2)29.先化简,再求值:(1)3a(2a2-4a+3)-2a2(3a+4),其中a=-2;解: 3a(2a2-4a+3)-2a2(3a+4)=6a3-12a2+9a-6a3-8a2=-20a2+9a当a=-2时,原式=-20×(-2)2+9×(-2)=-80-18=-98(2)(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6;解 (a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2=(a2-6ab+9b2)+(9a2+6ab+b2) – (a2 +10ab+25b2) +(a2-10ab+25b2)=a2-6ab+9b2 +9a2+6ab+b2 – a2 -10ab-25b2+a2-10ab+25b2=10a2+10b2-20ab=10(a-b)2当a=-8,b=-6时,原式=10×(-8+6)2=40.10.求下列各式的值:(1)(3x4-2x3)÷(-x)-(x-x2)·3x,其中x= .解:(3x4-2x3)÷(-x)-(x-x2)·3x=-3x3+2x2-(3x2-3x3)=-3x3+2x2-3x2+3x3=-x2B组10.求下列各式的值:(2)[(ab+1)(ab-2)-2a2b2+2]÷(-ab),其中a= ,b= ;解: [(ab+1)(ab-2)-2a2b2+2]÷(-ab)=[(ab+1)(ab-2)-2(a2b2-1)]÷(-ab)=ab+1=[(ab+1)(ab-2)-2(ab+1)(ab-1)]÷(-ab)=[(ab+1)[(ab-2)-2(ab-1)]]÷(-ab)=(ab+1)(-ab)÷(-ab)11.已知(x+y)2=1, (x-y)2=49,求x2+y2 与xy的值.解: ∵ (x+y)2=1∴x2+2xy+y2=1∵ (x-y)2=49∴x2-2xy+y2=49∴解得x2+y2=25,xy=-1212.已知a+b=3, ab=2,求a2+b2 的值.解: a2+b2=a2+b2+2ab-2ab=(a+b)2-2ab=32-2×2=513.已知a-b=1, a2+b2=25,求ab的值.解: ab=[-(a-b)2+a2+b2]÷2=(-12+25)÷2=1214.把下列多项式分解因式:(1)x(x+y)-y(x+y)(2)(a+b)2+2(a+b)+1(3)4x4+4x3+x2(4)x2-16ax+64a2=(x-y)(x+y)=(a+b+1)2=x2(4x2+4x+1)=x2(2x+1)2=(x2-8a)214.把下列多项式分解因式:(5)(x-1)(x-3)+1(6)(ab+a)+(b+1)=(x2-4x+3)+1=x2-4x+4=(x-2)2=a(b+1)+(b+1)=(a+1)(b+1)15.(1)一个正方形的边长增加3cm,它的面积增加了45cm2,求原来这个正方形的边长.(2)一个正方形的边长减少3cm,它的面积减少了45cm2,原来这个正方形的边长是多少呢?它和题(1)的答案相同吗?解:(1)设原边长为xcm,则(x+3)2-x2=45解得 x=6(cm)(2)设原边长为xcm,则x2-(x-3)2=45解得 x=9(cm)答案不相同16.已知一个长方形,若它的长增加4cm,宽减少1cm,则面积保持不变;若它的长减少2cm,宽增加1cm,则面积仍保持不变.求这个长方形的面积.解:设这个长方形的长与宽分别为acm和bcm依题意,得解得即长方形的面积为ab=8×3=24(cm2)C组17.已知M是含字母x的单项式,要使多项式4x2+M+1是某一个多项式的平方,求M.解:当M=±4x时或M=4x4时,4x2+M+1是一个多项式的平方.18.判断下列说法是否正确,并说明理由:(1)两个连续整数的平方差必是奇数;解:(1)正确.设两个连续的数分别为x,x+1,则它们的平方差表示为(x+1)2-x2=2x+1. 而当x为整数时,2x+1总是一个奇数.18.判断下列说法是否正确,并说明理由:(2)若a为整数,则a3-a能被6整除.解:(2)正确.因为a3-a=a(a+1)(a-1) 当a为整数时,a-1,a,a+1恰好为三个连续的整数,而任何三个连续整数中,必有一个能被3整除,且至少有一个偶数,能被2整除,故三个连续整数的乘积必能被6整除,即a3-a能被6整除.
章末复习华东师大版 八年级数学上册同底数幂的乘法aman=am+n幂的乘方(am)n=amn积的乘方(ab)n=anbn底数不变指数相加a既可以是数,也可以是“式”底数不变指数相乘与同底数幂的乘法不要混淆将积中每个因式分别乘方,再相乘 积中每个因式都要乘方,不要丢项一、幂的部分运算性质单项式乘以单项式单项式乘以多项式多项式乘以多项式2ab·3a=6a2b只在一个因式里含有的字母a(b+c)=ab+ac不要漏项(a+b)(c+d)=ac+ad+bc+bd注意符号二、整式的乘法三、乘法公式平方差公式完全平方公式(a+b)(a-b)=a2-b2(a±b)2=a2±2ab+b2字母a、b既可以是数,也可以是“式”中间项的符号与等号左边相同同底数幂的除法am÷an=am-n单项式除以单项式多项式除以单项式底数不变指数相减a0=1(a≠0)6a2b÷2a=3ab只在被除式里出现的字母(ma+mb+mc) ÷m=a+b+c①符号②不要漏项四、整式的除法1.计算:(1)a10·a8(2)(xy)2·(xy)3(3)[(-x)3]2(4)[(-x)2]3(5)(-2mn2)3(6)(y3)2·(y2)4=a10+8=a18=(xy)2+3=(xy)5=x5y5=(-x)6=x6=(-x)6=x6=-8m3n6=y6·y8=y14A组2.计算:(1)2a·3a2(2)(-3xy)·(-4yz)(3)(-2a2)2·(-5a3)(4)(-3x)·(2x2-x-1)=2·3a·a2=6a3=(-3)×(-4)xy·yz=12xy2z=4a4·(-5a3)=4×(-5)a4·a3=-20a7=(-3x)·2x2-(-3x)x-(-3x)=-6x3+3x2+3x2.计算:(5)(x-2)(x-6)(6)(2x-1)(3x+2)(7)(y-2)(y2-6y-9)(8)(p-6q)(p2+pq+q2)=(x-2)x-6(x-2)=x2-2x-6x+12=x2-8x+12=2x(3x+2)-(3x+2)=6x2+4x-3x-2=6x2+x-2=y(y2-6y-9)-2(y2-6y-9)=y3-6y2-9y-2y2+12y+18=y3-8y2+3y+18=p(p2+pq+q2)-6q(p2+pq+q2)=p3+p2q+pq2-6p2q-6pq2-6q3=p3-5p2q-5pq2-6q33.计算:(1)(x+2)(x-2)(2)(m+n)(m-n)(3)(-m-n)(-m+n)(4)(-m-n)(m+n)=x2-4=m2-n2=-(m+n)(n-m)=-(n2-m2)=-n2+m2=-(m+n)(m+n)=-(m2+2mn+n2)=-m2-2mn-n2(5)(-m+n)(m-n)=-(m-n)(m-n)=-(m2-2mn+n2)=-m2+2mn-n24.计算:(1)20132-2014×2012(2)(4×104)×(2×103)-(6.5×103)×(6×103)=20132-(2013+1)×(2013-1)=20132-20132+1=1=8×104×103-39×103×103=8×107-3.9×107=4.1×1074.计算:(3)(2x+5)2-(2x-5)2=(2x+5-2x+5)(2x+5+2x-5)=10·4x=40x= -4x4.计算:(6)(-6x2)2+(-3x)3·x=2x2y+3xy-x2y=3xy+x2y=36x4-27x3·x=9x45.计算:(1)a·a4÷a3(2)(-x)6÷(-x)2·(-x)3(3)27x8÷3x4(4)-12m3n3÷4m2n3=a5÷a3=a2= (-x)6-2+3=-x7=9x8-4=9x4=-3m3-2n3-3=-3m5.计算:(5)(6x2y3z2)2÷4x3y4(6)(-6a2b5c)÷(-2ab2)2=36x4y6z4÷4x3y4=9x4-3y6-4z4=9xy2z4=(-6a2b5c)÷4a2b4=-1.5a2-2b5-4c=-1.5bc6.计算:(1)(6a4-4a3-2a2)÷(-2a2)(2)(4x3y+6x2y2-xy3)÷2xy=6a4÷(-2a2)-4a3÷(-2a2)-2a2÷(-2a2)=-3a2+2a+1=4x3y÷2xy+6x2y2÷2xy-xy3÷2xy=2x2+3xy-0.5y26.计算:(4)(2ab2-b3)2÷2b3=4x2+8x-2=(4a2b4-4ab5+b6)÷2b3=4a2b4÷2b3-4ab5÷2b3+b6÷2b3=2a2b-2ab2+0.5b37.计算:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x.解: [(x-2y)[(x-2y)+(x+2y)]-2x(2x-y)]÷2x.=[2x(x-2y)-2x(2x-y)]÷2x.=2x(x-2y-2x+y)÷2x.=-x-y8.把下列多项式分解因式:(1)x2-25x(2)2x2y2-4y3z(3)am-an+ap(4)x3-25x=x(x-25)=2y2(x2-2yz)=a(m-n+p)=x(x2-25)=x(x+5)(x-5)8.把下列多项式分解因式:(5)1-4x2(6)25x2+20xy+4y2(7)x3-4x2+4x=(1-2x)(1+2x)=(5x+2y)2=x(x2-4x+4)=x(x-2)29.先化简,再求值:(1)3a(2a2-4a+3)-2a2(3a+4),其中a=-2;解: 3a(2a2-4a+3)-2a2(3a+4)=6a3-12a2+9a-6a3-8a2=-20a2+9a当a=-2时,原式=-20×(-2)2+9×(-2)=-80-18=-98(2)(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6;解 (a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2=(a2-6ab+9b2)+(9a2+6ab+b2) – (a2 +10ab+25b2) +(a2-10ab+25b2)=a2-6ab+9b2 +9a2+6ab+b2 – a2 -10ab-25b2+a2-10ab+25b2=10a2+10b2-20ab=10(a-b)2当a=-8,b=-6时,原式=10×(-8+6)2=40.10.求下列各式的值:(1)(3x4-2x3)÷(-x)-(x-x2)·3x,其中x= .解:(3x4-2x3)÷(-x)-(x-x2)·3x=-3x3+2x2-(3x2-3x3)=-3x3+2x2-3x2+3x3=-x2B组10.求下列各式的值:(2)[(ab+1)(ab-2)-2a2b2+2]÷(-ab),其中a= ,b= ;解: [(ab+1)(ab-2)-2a2b2+2]÷(-ab)=[(ab+1)(ab-2)-2(a2b2-1)]÷(-ab)=ab+1=[(ab+1)(ab-2)-2(ab+1)(ab-1)]÷(-ab)=[(ab+1)[(ab-2)-2(ab-1)]]÷(-ab)=(ab+1)(-ab)÷(-ab)11.已知(x+y)2=1, (x-y)2=49,求x2+y2 与xy的值.解: ∵ (x+y)2=1∴x2+2xy+y2=1∵ (x-y)2=49∴x2-2xy+y2=49∴解得x2+y2=25,xy=-1212.已知a+b=3, ab=2,求a2+b2 的值.解: a2+b2=a2+b2+2ab-2ab=(a+b)2-2ab=32-2×2=513.已知a-b=1, a2+b2=25,求ab的值.解: ab=[-(a-b)2+a2+b2]÷2=(-12+25)÷2=1214.把下列多项式分解因式:(1)x(x+y)-y(x+y)(2)(a+b)2+2(a+b)+1(3)4x4+4x3+x2(4)x2-16ax+64a2=(x-y)(x+y)=(a+b+1)2=x2(4x2+4x+1)=x2(2x+1)2=(x2-8a)214.把下列多项式分解因式:(5)(x-1)(x-3)+1(6)(ab+a)+(b+1)=(x2-4x+3)+1=x2-4x+4=(x-2)2=a(b+1)+(b+1)=(a+1)(b+1)15.(1)一个正方形的边长增加3cm,它的面积增加了45cm2,求原来这个正方形的边长.(2)一个正方形的边长减少3cm,它的面积减少了45cm2,原来这个正方形的边长是多少呢?它和题(1)的答案相同吗?解:(1)设原边长为xcm,则(x+3)2-x2=45解得 x=6(cm)(2)设原边长为xcm,则x2-(x-3)2=45解得 x=9(cm)答案不相同16.已知一个长方形,若它的长增加4cm,宽减少1cm,则面积保持不变;若它的长减少2cm,宽增加1cm,则面积仍保持不变.求这个长方形的面积.解:设这个长方形的长与宽分别为acm和bcm依题意,得解得即长方形的面积为ab=8×3=24(cm2)C组17.已知M是含字母x的单项式,要使多项式4x2+M+1是某一个多项式的平方,求M.解:当M=±4x时或M=4x4时,4x2+M+1是一个多项式的平方.18.判断下列说法是否正确,并说明理由:(1)两个连续整数的平方差必是奇数;解:(1)正确.设两个连续的数分别为x,x+1,则它们的平方差表示为(x+1)2-x2=2x+1. 而当x为整数时,2x+1总是一个奇数.18.判断下列说法是否正确,并说明理由:(2)若a为整数,则a3-a能被6整除.解:(2)正确.因为a3-a=a(a+1)(a-1) 当a为整数时,a-1,a,a+1恰好为三个连续的整数,而任何三个连续整数中,必有一个能被3整除,且至少有一个偶数,能被2整除,故三个连续整数的乘积必能被6整除,即a3-a能被6整除.
相关资料
更多









