华师大版九年级上册3.列举所有机会均等的结果精品ppt课件

这是一份华师大版九年级上册3.列举所有机会均等的结果精品ppt课件，共16页。PPT课件主要包含了第①枚，树状图，第1次摸出球，第2次摸出球，画出如图的树状图等内容，欢迎下载使用。

学习目标： 理解并掌握列表法和树状图法求随机事件的概率，并利用它们解决问题，正确认识在什么条件下使用列表法，什么条件下使用树状图法.
学习重点：会用列表法和树状图法求随机事件的概率.区分什么时候用列表法，什么时候用树状图法求概率.
学习难点：列表法是如何列表，树状图的画法.列表法和树状图的选取方法.
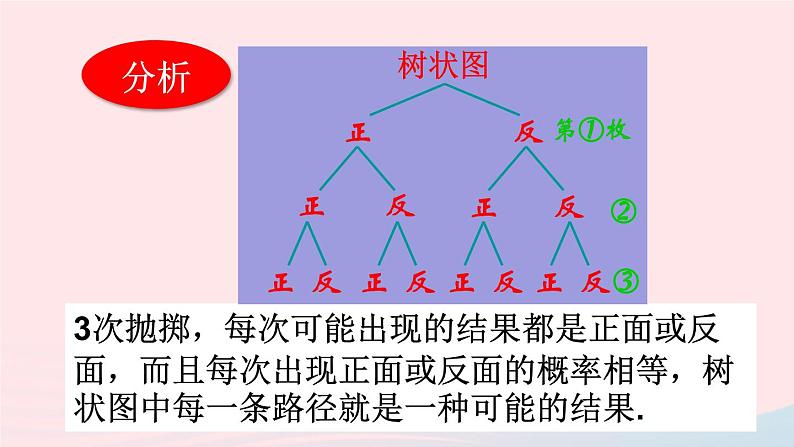
抛掷一枚普通硬币3次.有人说“连续掷出三个正面”和“先掷出两个正面，再掷出一个反面”的概率是一样的.你同意吗？
3次抛掷，每次可能出现的结果都是正面或反面，而且每次出现正面或反面的概率相等，树状图中每一条路径就是一种可能的结果.
有的同学认为：抛掷三枚普通硬币，硬币落地后只可能出现4种结果：(1)全是正面；(2)两正一反；(3)两反一正；(4)全是反面.因此这四个事件出现的概率相等.你同意这种说法吗？为什么？
不同意；四种情况出现的概率并不均等，(1)(4)出现的几率要小于(2)(3).
口袋中装有1个红球和2个白球，搅匀后从中摸出1个球，放回搅匀，再摸出第2个球，两次摸球就可能出现3种结果：(1)都是红球；(2)都是白球；(3)一红一白.这三个事件发生的概率相等吗?
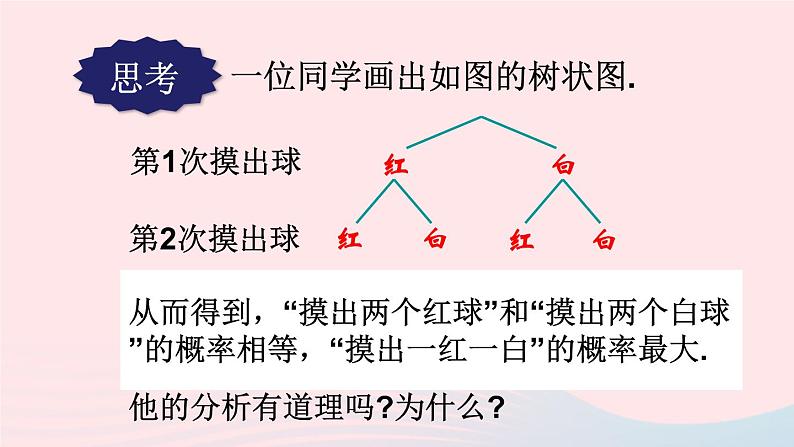
一位同学画出如图的树状图.
从而得到，“摸出两个红球”和“摸出两个白球”的概率相等，“摸出一红一白”的概率最大.
他的分析有道理吗?为什么?
把两个白球分别记作白1和白2，画出如下的树状图.
从图中可以看出，一共有9种等可能的结果.
投掷两枚普通的正方体骰子.掷得的点数之积有多少种可能？点数之积为多少的概率最大，其概率是多少?
用列举法来得出所有可能的点数之积.
“石头、剪刀、布”的游戏中，假定甲乙两人每次都是等可能地做这三种手势，那么一次比赛两人做同种手势(即不分胜负)的概率是多少?
1.同时投掷两枚普通的正四面体骰子，求下列事件的概率:(1)所得点数之和恰为偶数；(2)所得点数之和恰为奇数；(3)所得点数之和恰为质数；
2.在九九乘法表的45个运算结果中随意抽取1个，将下列事件的概率从小到大排序：(1)恰为偶数；(2)恰为奇数；(3)小于10；(4)大于100；(5)个位数是0；(6)3的倍数.
1.一次试验中可能出现的结果是有限多个，各种结果发生的可能性是相等的.通常可用列表法和树状图法求得各种可能结果. 2.注意第二次放回与不放回的区别. 3.一次实验中涉及3个或更多个因素时，不重不漏地求出所有可能的结果，通常采用树状图法.