湖南省岳阳市岳阳楼区湘一南湖学校2022-2023学年八年级下学期第二次月考数学试题(无答案)

这是一份湖南省岳阳市岳阳楼区湘一南湖学校2022-2023学年八年级下学期第二次月考数学试题(无答案)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
时量：90分钟 命题人：胡竞宇 审题人：谢凤芳
一、选择题（本大题共8小题，在每小题给出的四个选项中，只有一个选项符合题意。）
1．下列各组数中，是勾股数的一组是（ ）
A．1，1，2 B．5，7，9 C．6，8，10 D．6，12，14
2．中华文化底蕴深厚，地方文化活动丰富多彩．下面的四幅简笔画是从我国地方文化活动中抽象出来的，其中是中心对称图形的是（ ）
A． B． C． D．
3．一次函数y＝﹣3x+1的图象经过（ ）
A．一、二、三象限 B．一、三、四象限 C．一、二、四象限 D．二、三、四象限
4．下列5个数：、 、 、、（﹣1）2021中，无理数出现的频数是（ ）
A．2 B．3 C．0.4 D．0.6
5．在平面直角坐标系内，已知点A（m+1，﹣2）和点B（3，m﹣1），且AB∥x轴，则m的值为（ ）
A．2 B．﹣1 C．﹣4 D．3
6．如图，在△ABC中，∠A＝90°，BE是△ABC的角平分线，ED⊥BC于点D，CD＝4，△CDE周长为12，则AC的长是（ ）
A．14 B．8 C．16 D．6
7．下列命题为真命题的是（ ）
A．一组对边平行的四边形是平行四边形
B．平行四边形的对角线平分每一组对角
C．平行四边形既是轴对称图形，又是中心对称图形
D．平行四边形的对角线互相平分
8．已知过点（2，3）的直线y＝ax+b（a≠0）不经过第四象限，设S＝a+2b，则S的取值范围为（ ）
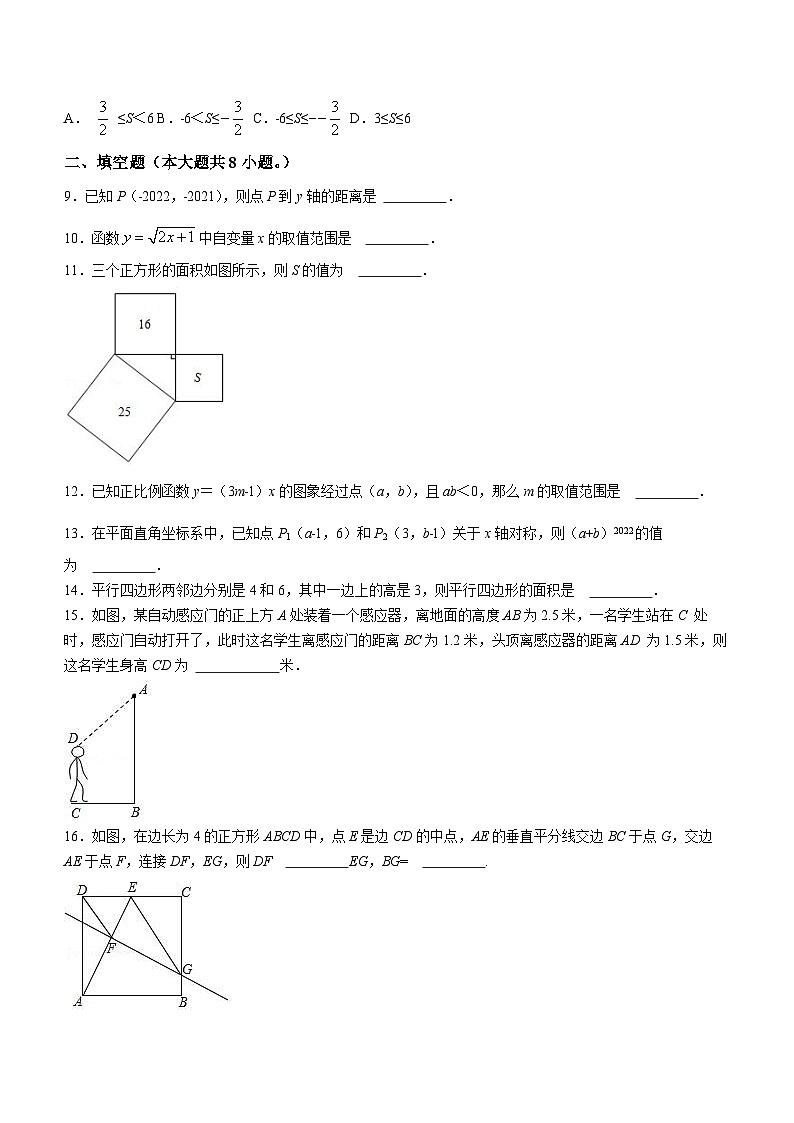
A． ≤S＜6 B．﹣6＜S≤ C．﹣6≤S≤− D．3≤S≤6
二、填空题（本大题共8小题。）
9．已知P（﹣2022，﹣2021），则点P到y轴的距离是 ．
10．函数中自变量x的取值范围是 ．
11．三个正方形的面积如图所示，则S的值为 ．

12．已知正比例函数y＝（3m﹣1）x的图象经过点（a，b），且ab＜0，那么m的取值范围是 ．
13．在平面直角坐标系中，已知点P1（a﹣1，6）和P2（3，b﹣1）关于x轴对称，则（a+b）2022的值为 ．
14．平行四边形两邻边分别是4和6，其中一边上的高是3，则平行四边形的面积是 ．
15．如图，某自动感应门的正上方A处装着一个感应器，离地面的高度AB为2.5米，一名学生站在C 处时，感应门自动打开了，此时这名学生离感应门的距离BC为1.2米，头顶离感应器的距离AD 为1.5米，则这名学生身高CD为 米．

16．如图，在边长为4的正方形ABCD中，点E是边CD的中点，AE的垂直平分线交边BC于点G，交边AE于点F，连接DF，EG，则DF EG，BG= .
三、解答题（本大题共8小题。）
17．计算：．
18．如图，平行四边形ABCD对角线上有两点E，F，AE＝CF， ，连接BD交AC于点O，EB，ED，FB，FD．
（1）请在横线上添加一个合适的条件（不另加辅助线），使得四边形EBFD为菱形；
（2）添加条件后，证明四边形EBFD为菱形．
19．如图，已知一次函数y=x+3的图象与x轴，y轴分别交于A，B两点．点C（4，n）在该函数的图象上，连接OC．
（1）直接写出点A，B的坐标为：A（ ），B（ ）；
（2）求△OAC的面积．
20．某学校为了解学生关于新冠病毒防疫常识的掌握情况，特开展了网络防疫测试．某小组随机抽取部分学生的测试成绩x（满分100分），并进行整理分析，绘制了如下尚不完整的统计图表．
学生测试成绩频数分布表
根据以上信息，回答下列问题：（1）本次共抽取了 名学生的测试成绩．
（2）m＝ ，n＝ ．
（3）若成绩低于80分，视为对防疫常识了解不到位，根据以上信息，分析学生对防疫常识的了解情况，并向学校提出合理化建议．
21．为激发同学们对航天事业的兴趣，学校打算购买一些“飞天”装饰挂件与专属航天印章送给学生留作纪念．已知每盒挂件有30个，每盒印章有20个，且都只能整盒购买，每盒挂件的价钱比每盒印章的价钱多10元；用200元购买挂件的盒数与用150元购买印章的盒数相同．
（1）求每盒挂件和每盒印章的价格分别为多少元？
（2）如果给每位学生分发2个挂件与2个印章．设购买挂件a盒，购买印章b盒恰好能配套分发，请用含a的代数式表示b；
（3）累计购买超过850元后，超出850元的部分有6折的优惠．学校以（2）中的配套方式购买，共需要花费w元，求w关于a的函数关系式．该校有750名学生，需要购买挂件与印章各多少盒？共需要多少费用？
22．图1是超市购物车，图2为超市购物车侧面示意图，测得∠ACB＝90°，支架AC＝4.8dm，CB＝3.6dm．
（1）两轮中心AB之间的距离为 dm；
（2）若OF的长度为 dm，支点F到底部DO的距离为5dm，试求∠FOD的度数．
23．在边长为5的正方形ABCD中，点E在边CD所在直线上，连接BE，以BE为边，在BE的下方作正
方形BEFG，并连接AG．
（1）如图1，当点E与点D重合时，AG＝ ；
（2）如图2，当点E在线段CD上时，DE＝2，求AG的长；
（3）若AG= ，请直接写出此时DE的长．
24.如图，直线y＝kx+k分别交x轴、y轴于点A，C，直线BC过点C交x轴于点B，且OA= OC，∠CBA ＝45°，点P是直线BC上的一点．
（1）求直线BC的解析式；
（2）若动点P从点B出发沿射线BC方向匀速运动，速度为 个单位长度/秒，连接AP，设△PAC 的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出t的取值范围；
（3）若点Q是直线AC上且位于第三象限图象上的一个动点，点M是y轴上的一个动点，当以点B、 M、Q为顶点的三角形为等腰直角三角形时，求点Q和点M的坐标．
组别
成绩x/分
人数
A
60≤x＜70
n
B
70≤x＜80
9
C
80≤x＜90
12
D
90≤x≤100
6