精品解析：广东省深圳市南山区前海港湾学校2022-2023学年八年级上学期期中考试数学试卷

南山区前海港湾学校2022-2023学年第一学期八年级期中考试数学试卷

一．选择题（每题3分，共30分）

1. 下列各数组中，能作为直角三角形三边长的是（　　）

A. 9，13，15 B. 3，3， C. 15，9，17 D. 3，4，5

【答案】D

【解析】

【分析】根据勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．

详解】解：A． ，不能构成直角三角形，故本选项不符合题意；

B． ，不能构成直角三角形，故本选项不符合题意；

C． ，不能构成直角三角形，故本选项不符合题意；

D． ，能构成直角三角形，故本选项符合题意；

故选：D．

【点睛】本题主要考查利用勾股定理的逆定理判断能否构成直角三角形，熟练掌握勾股定理逆定理是解题的关键．

2. 下列各数中是无理数的是（　　）

A.  B.  C. 0 D.

【答案】A

【解析】

【分析】根据无理数的定义（无限不循环小数是无理数）逐项判断即可得．

【详解】解：A、是无理数，则此项符合题意；

B、是无限循环小数，属于有理数，则此项不符合题意；

C、0是整数，属于有理数，则此项不符合题意；

D、是有限小数，属于有理数，则此项不符合题意；

故选：A．

【点睛】本题考查了无理数，熟记无理数定义是解题关键．

3.  等于（　　）

A. ±4 B. 4 C. ±4 D. 4

【答案】D

【解析】

【分析】根据立方根的定义计算即可．

【详解】因为，

所以A、B、C都错误，D正确，

故选D．

【点睛】本题考查了求一个数的立方根，熟练掌握立方根的计算是解题的关键．

4. 下列计算中，正确的是（　　）

A.  B.  C.  D.

【答案】B

【解析】

【分析】根据算术平方根和二次根式的运算法则去判断即可．

【详解】解：A、，故此选项不符合题意；

B、，故此选项符合题意；

C、，故此选项不符合题意；

D、，故此选项不符合题意．

故选：B．

【点睛】此题主要考查了二次根式的运算，熟练掌握二次根式的运算法则是解题的关键．

5. 若点P（m，2）与点Q（3，n）关于y轴对称，则m，n值分别为（　　）

A. ﹣3，2 B. 3，﹣2 C. ﹣3，﹣2 D. 3，2

【答案】A

【解析】

【分析】根据平面直角坐标系中关于y轴对称的点的坐标特点即可求m，n的值．

【详解】∵点与点关于y轴对称，

∴m+3=0，n=2，

∴m=-3，n=2，

故选：A．

【点睛】本题考查平面直角坐标系中关于y轴对称的点的坐标特点，如果两个点关于y轴对称，则横坐标互为相反数，纵坐标相等．

6. 若二次根式有意义，则字母a应满足的条件是（　　）

A.  B.  C.  D.

【答案】D

【解析】

【分析】根据二次根式有意义的条件，得到，解不等式即可．

【详解】因为二次根式有意义，

所以，

解得，

故选D．

【点睛】本题考查了二次根式有意义的条件，熟练掌握有意义的基本条件是解题的关键．

7. 下列二次根式中，与是同类二次根式的是（　　）

A.  B.  C.  D.

【答案】B

【解析】

【分析】直接利用同类二次根式的定义分别化简二次根式求出答案．

【详解】解：A、，与不是同类二次根式，故该选项不符合题意；

B、，与，是同类二次根式，故该选项符合题意；

C、，与不是同类二次根式，故该选项不符合题意；

D、，与不是同类二次根式，故该选项不符合题意；

故选：B．

【点睛】此题主要考查了同类二次根式，解题的关键是正确化简二次根式．

8. 下列函数中，是一次函数的是（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据一次函数的一般形式对各选项依次进行判断．

【详解】解：一次函数的一般形式为：，（、是常数，）

选项C符合题意

故选：C

【点睛】本题考查了一次函数的识别，一次函数的一般形式为，（、是常数，），掌握一次函数的一般形式是解题关键．

9. 若点在第一象限，则点在（　　）

A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

【答案】D

【解析】

【分析】先根据所在象限判断出、与零的大小关系，然后再判断的横纵坐标的正负情况即可．

【详解】解：∵在第一象限

∴

则

故点的横坐标为正数，纵坐标为负数，点在第四象限

故选：D

【点睛】本题考查了判断坐标轴中的点所在象限，正确判断点的横、纵坐标正负号是解题关键．

10. 细心观察图形，可以计算出：

，

，

，

……

．则的周长为（　　）

A.  B.  C.  D.

【答案】B

【解析】

【分析】观察题目中的规律可得，，即可求解．

【详解】解：根据题意得：，，

∴的周长为．

故选B．

【点睛】本题主要考查了勾股定理的应用，明确题意，准确得到线段的变化规律是解题的关键．

二．填空题（每题3分，共15分）

11. 的平方根是       ．

【答案】±2

【解析】

【详解】解：∵

∴的平方根是±2．

故答案为±2．

12. 比较大小：_____．（填＞，＜，＝）

【答案】

【解析】

【分析】根据实数比较大小的方法求解即可．

【详解】解：∵，

∴，

故答案：．

【点睛】本题主要考查了实数比较大小，熟知实数比较大小的方法是解题的关键．

13. 有一个水池，水面是一个边长为10 m的正方形，在水池正中央有一根新生的芦苇，它高出水面1m，如果将这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．这个水池的深度是_____m．

【答案】12

【解析】

【分析】首先设水池的深度为m，则这根芦苇的长度为m，根据勾股定理可得方程，求解即可．

【详解】解：设水池的深度为m，由题意得：

，

解得：，

故答案为：12．

【点睛】本题主要考查了勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，能从题中抽象出勾股定理这一数学模型是解题的关键．

14. 在平面直角坐标系中，点到轴的的距离与到y轴的距离相等，则_______．

【答案】-1或-2

【解析】

【分析】根据点A到x轴的距离与到y轴的距离相等可得2a+3=1或2a+3=-1，据此解出a的值．

【详解】解：∵A到x轴的距离与到y轴的距离相等，
∴2a+3=1或2a+3=-1，
解得a=-1或a=-2．
故答案为：-1或-2．

【点睛】本题考查了点的坐标，关键是掌握到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值．

15. 观察下列运算过程：

……

请运用上面的运算方法计算：

＝_____．

【答案】

【解析】

【分析】根据运算方法可得到，然后按照规律计算即可．

【详解】解：∵

∴

=

=

=

故答案为：

【点睛】本题考查了计算规律探究、分母有理化、平方差公式，发现计算规律并正确运用是解题关键．

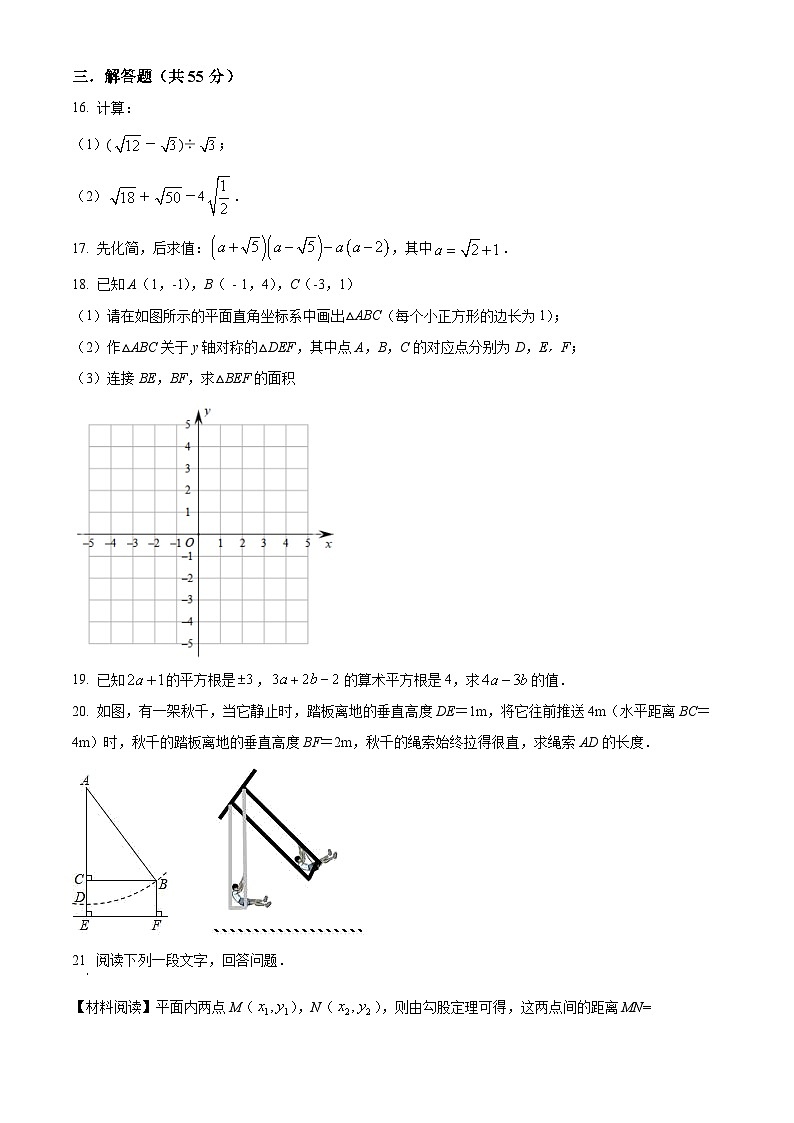
三．解答题（共55分）

16. 计算：

（1）(－)÷；

（2）＋－4．

【答案】（1）1    （2）

【解析】

【分析】（1）根据二次根式的性质和混合运算进行解答即可；

（2）根据二次根式的性质和加减混合运算进行解答即可．

【小问1详解】

解：原式；

【小问2详解】

解：原式＝3＋5－2＝．

【点睛】本题考查二次根式的化简及混合运算，熟练掌握二次根式混合运算的法则是解题的关键．

17. 先化简，后求值：，其中．

【答案】，

【解析】

【分析】先按照整式乘法运算法则化简，然后将代入计算即可．

详解】解：

=

=

将代入得

=

【点睛】本题考查了整式化简求值、平方差公式计算，掌握整式乘法运算法则是解题关键．

18. 已知A（1，-1），B（ - 1，4），C（-3，1）

（1）请在如图所示的平面直角坐标系中画出△ABC（每个小正方形的边长为1）；

（2）作△ABC关于y轴对称的△DEF，其中点A，B，C的对应点分别为D，E，F；

（3）连接BE，BF，求△BEF的面积

【答案】（1）画图见解析；（2）画图见解析；（3）3

【解析】

【分析】（1）根据A（1，-1），B（ - 1，4），C（-3，1）在坐标系内描出A，B，C，再顺次连接A，B，C即可；

（2）分别确定A，B，C关于轴的对称点D，E，F，再顺次连接D，E，F即可；

（3）利用三角形的面积公式直接计算即可得到答案.

【详解】解：（1）如图，即为所求作的三角形，

（2）如图，即为所求作的三角形，

（3）△BEF的面积

【点睛】本题考查的是坐标与图形，画关于轴对称的三角形，三角形面积的计算，掌握轴对称图形的性质是解题的关键.

19. 已知的平方根是，的算术平方根是4，求的值．

【答案】7

【解析】

【分析】根据平方根，算术平方根的定义，列式确定a，b的值，代入计算即可．

【详解】∵，

∴，

解得，

∴．

故答案为：7．

【点睛】本题考查了平方根即，称x是a的平方根，算术平方根即正的平方根，熟练掌握定义是解题的关键．

20. 如图，有一架秋千，当它静止时，踏板离地的垂直高度DE＝1m，将它往前推送4m（水平距离BC＝4m）时，秋千的踏板离地的垂直高度BF＝2m，秋千的绳索始终拉得很直，求绳索AD的长度．

【答案】绳索AD的长度为8.5m

【解析】

【分析】设秋千的绳索长为xm，根据题意可得AC＝（x﹣1）m，利用勾股定理可得x2＝42+（x﹣1）2，解方程即可．

【详解】解：在Rt△ACB中AC2+BC2＝AB2，

设秋千的绳索长为xm，则AC＝（x﹣1）m，

故x2＝42+（x﹣1）2，

解得：x＝8.5，

答：绳索AD的长度是8.5m．

【点睛】本题考查了勾股定理的实际应用中的秋千问题，根据题意作出秋千运动前后的图形，构造直角三角形运用勾股定理解答是关键．

21. 阅读下列一段文字，回答问题．

【材料阅读】平面内两点M（），N（），则由勾股定理可得，这两点间的距离MN=．例如，M（3，1），N（1，－2），则MN=

【直接应用】

（1）已知P（2，－3），Q（－1，3），求P、Q两点间的距离；

（2）如图，在平面直角坐标系中，A（－1，－3），OB=，OB与轴正半轴的夹角是45°．

①求点B的坐标；

②试判断△ABO的形状．

【答案】（1）   

（2）①B（1，−1）；△ABO是直角三角形．

【解析】

【分析】（1）由两点间的距离公式可求出答案；

（2）①过点B作BF⊥y轴于点F，求出OF＝BF＝1，则可求出答案；

②求出OA和AB的长，由勾股定理的逆定理可得出结论．

【小问1详解】

解：∵P（2，−3），Q（−1，3），

∴PQ＝；

【小问2详解】

①过点B作BF⊥y轴于点F，

∵OB与x轴正半轴的夹角是45°，

∴∠FOB＝∠OBF＝45°，

∵OB＝，

∴OF＝BF＝1，

∴B（1，−1）；

②∵A（−1，−3），B（1，−1），

∴OA＝

，AB＝，

∵AB2＋OB2＝8＋2＝10，OA2＝10，

∴AB2＋OB2＝OA2，

∴△ABO是直角三角形．

【点睛】本题考查了勾股定理，直角三角形的性质，坐标与图形的性质，两点间的距离公式，熟练掌握勾股定理是解题的关键．

22. 在平面直角坐标系中，O为坐标原点，过点A（8,6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．

（1）直接写出点B和点C的坐标：B（       ，        ）C（       ，         ）．

（2）当点P运动时，用含t的代数式表示线段AP的长，并写出t的取范围；

（3）点D（2,0），连结PD、AD，在（2）的条件下是否存在这样的t值，使S△APD=S四边形ABOC，若存在，请求t值，若不存在，请说明理由．

【答案】（1）B（0,6）C（8,0）

（2）

 （3）3,5

【解析】

【分析】（1）根据题意即可得到结论；

（2）当点P在线段BA上时，根据A（8，6），B（0，6），C（8，0），得到AB=8，AC=6当点P在线段AC上时，于是得到结论；

（3）当点P在线段BA上时，当点P在线段AC上时，根据三角形的面积公式即可得到结论．

【详解】（1）B（0，6），C（8，0），

故答案为0、6，8、0；

（2）当点P在线段BA上时，

由A（8，6），B（0，6），C（8，0）可得：AB=8，AC=6，

∵AP=AB-BP，BP=2t，

∴AP=8-2t（0≤t＜4）；

当点P在线段AC上时，

∵AP=点P走过的路程-AB=2t-8（4≤t≤7）；

（3）存在两个符合条件的t值，

当点P在线段BA上时，

∵S△APD=AP•AC，SABOC=AB•AC，

∴•（8-2t）×6=×8×6，

       解得：t=3＜4，

当点P在线段AC上时，

∵S△APD=AP•CD，CD=8-2=6，

∴•（2t-8）×6=×8×6，

解得：t=5＜7，综上所述：当t为3秒和5秒时S△APD=SABOC，

【点睛】本题考查了坐标与图形性质，矩形的性质，三角形面积的计算，正确的作出图形是解题的关键．