精品解析：广东省深圳市南山区太子湾学校2022-2023学年八年级上学期期中考试数学试题

2022-2023学年度第一学期太子湾学校期中教学质量监测

八年级数学试题

一、选择题（共10小题，30分）

1. 使有意义的x的取值范围是（　　）

A.  B.  C.  D.

2. 下列数据不能确定物体位置的是（    ）

A 4行5列 B. 东北方向

C. 青年东路25号 D. 东经118°，北纬40°

3. 下列运算中错误的是（        ）

①；②；③；④；⑤

A ②③ B. ①④ C. ②④ D. ③⑤

4. 新冠疫情防控形势下，学校要求学生每日测量体温．某同学连续一周的体温情况如表所示，则该同学这一周的体温数据的众数和中位数分别是（　　）

A 36.3和36.2 B. 36.2和36.3 C. 36.3和36.3 D. 36.2和36.1

5. 如图，若AB∥CD，则α、β、γ之间的关系为（    ）

A. α+β+γ=360° B. α﹣β+γ=180° C. α+β﹣γ=180° D. α+β+γ=180°

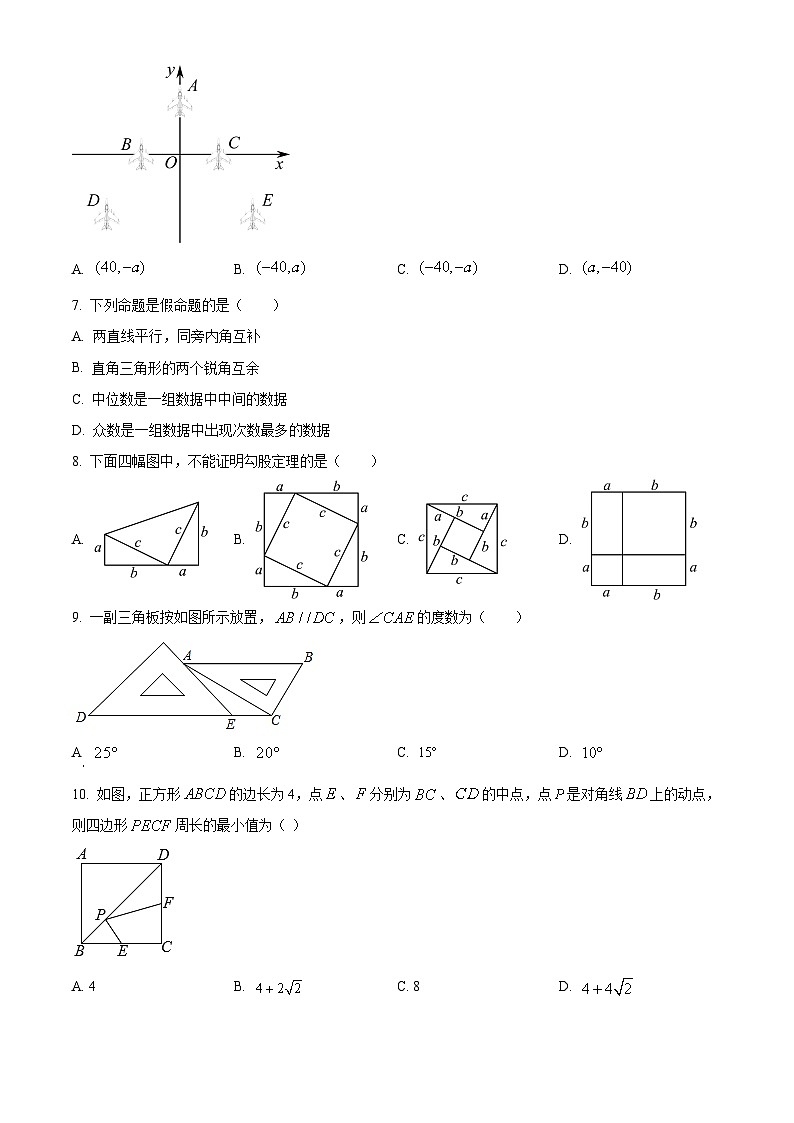
6. 如图是战机在空中展示的轴对称队形．以飞机B，C所在直线为x轴、队形的对称轴为y轴，建立平面直角坐标系．若飞机E的坐标为(40，a)，则飞机D的坐标为（    ）

A.  B.  C.  D.

7. 下列命题是假命题的是（　　）

A. 两直线平行，同旁内角互补

B. 直角三角形的两个锐角互余

C. 中位数是一组数据中中间的数据

D. 众数是一组数据中出现次数最多的数据

8. 下面四幅图中，不能证明勾股定理的是（    ）

A.  B.  C.  D.

9. 一副三角板按如图所示放置，，则的度数为（    ）

A  B.  C.  D.

10. 如图，正方形的边长为4，点、分别为、的中点，点是对角线上的动点，则四边形周长的最小值为（ ）

A. 4 B.  C. 8 D.

二、填空题（共5小题，共15分）

11. 比较大小：__________； ___________1．（填“>”“＜”或“=”）

12. 一个正数a的两个平方根分别是与，则a的值为_________．

13. 点A（3，﹣4）到x轴的距离是_________

14. 《九章算术》中一道“引葭赴岸”问题：“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个池塘，其地面是边长为10尺的正方形，一棵芦苇AC生长在它的中央，高出水面部分BC为1尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部C恰好碰到岸边的处（如图），水深和芦苇长各多少尺？则该问题的水深是___________尺．

15. 如图，一只蚂蚁从长为、宽为、高为的长方体纸箱外壁的A点沿纸箱爬到纸箱内壁的B点，，那么它所行的最短路线长是___________．

三、解答题（共7小题，55分）

16. 计算：

（1）；

（2）

17. 如图，，，点B在x轴上，且．

（1）求点B的坐标；

（2）求的面积；

（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为7？若存在，请直接写出点P的坐标；若不存在，请说明理由．

18. 某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：

(1)本次接受随机抽样调查的学生人数为___，图①中m的值是___；

(2)求本次你调查获取的样本数据的平均数、众数和中位数；

(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数．

19. 如图，每个小正方形的边长都为1．

（1）求四边形ABCD的周长及面积；

（2）求∠BCD的度数．

20. 如图，△ABC中，∠A=40°，

(1)若点P是∠ABC与∠ACB平分线的交点，求∠P的度数；

(2)若点P是∠CBD与∠BCE平分线的交点，求∠P的度数；

(3)若点P是∠ABC与∠ACF平分线的交点，求∠P的度数；

(4)若∠A=β，求(1)(2)(3)中∠P的度数(用含β的代数式表示，直接写出结果)

21. 小明在解决问题：已知，求的值．他是这样分析与解的：

∵，

∴，

∴，

∴，

∴．

请你根据小明的分析过程，解决如下问题：

（1）化简

（2）若，

①求的值；

②直接写出代数式的值___________．

22. 如图1，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s．

（1）连接AQ、CP交于点M，则在P、Q运动的过程中，∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数；

（2）何时△PBQ是直角三角形？

（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠CMQ变化吗？若变化，则说明理由，若不变，则求出它的度数．