精品解析：广东省深圳市宝安区2022-2023学年九年级上学期数学期中考试模拟试卷

这是一份精品解析：广东省深圳市宝安区2022-2023学年九年级上学期数学期中考试模拟试卷，文件包含精品解析广东省深圳市宝安区2022-2023学年九年级上学期数学期中考试模拟试卷原卷版docx、精品解析广东省深圳市宝安区2022-2023学年九年级上学期数学期中考试模拟试卷解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
广东省深圳市宝安区2022-2023学年第一学期九年级数学期中考试模拟试卷一、选择题（共10题；共30分）1. 一元二次方程的解是（ ）A. x1=0，x2=1 B. x=0C. x=2 D. x1=0，x2=2【答案】D【解析】【分析】先把方程直接开平方得到x-1=±1，再求x值即可.【详解】∵∴x−1=±1，∴x1=0,x2=2.故选：D.【点睛】考查一元二次方程的解法—直接开方法，熟练掌握一元二次方程的解法是解题的关键.2. 如图所示，该几何体的俯视图是（    ）A.  B.  C.  D. 【答案】B【解析】【分析】根据俯视图的定义判断即可．【详解】俯视图即从上往下看的视图,因此题中的几何体从上往下看是左右对称的两个矩形．故选B．【点睛】本题考查俯视图的定义,关键在于牢记定义．3. 小明把如图所示的平行四边形纸板挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上，且落在纸板 的任何一个点的机会都相等），则飞镖落在阴影区域的概率是（  ）A.  B.  C.  D. 【答案】C【解析】【详解】试题解析：根据平行四边形的性质可得：平行四边形的对角线把平行四边形分成的四个面积相等的三角形，根据平行线的性质可得 S1=S2， 则阴影部分的面积占， 故飞镖落在阴影区域的概率为：； 故选C．考点：1．几何概率；2．平行四边形的性质．4. 如图，l1∥l2∥l3，直线a，b与l1，l2，l3分别交于点A，B，C和点D，E，F．若，DE＝4，则DF的长是（    ）A.  B.  C. 6 D. 10【答案】D【解析】【分析】利用平行线分线段成比例定理列出比例式，求出EF，结合图形计算即可．【详解】解：∵l1∥l2∥l3，∴＝＝，又DE＝4，∴EF＝6，∴DF＝DE+EF＝10，故选：D．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．5. 用配方法解方程时，原方程变形正确的是（　　）A.  B.  C.  D. 【答案】A【解析】【分析】方程常数项移到右边，两边加上一次项系数一半的平方，利用完全平方公式变形得到结果，即可做出判断．【详解】解：方程，
变形得：，
配方得：，即，
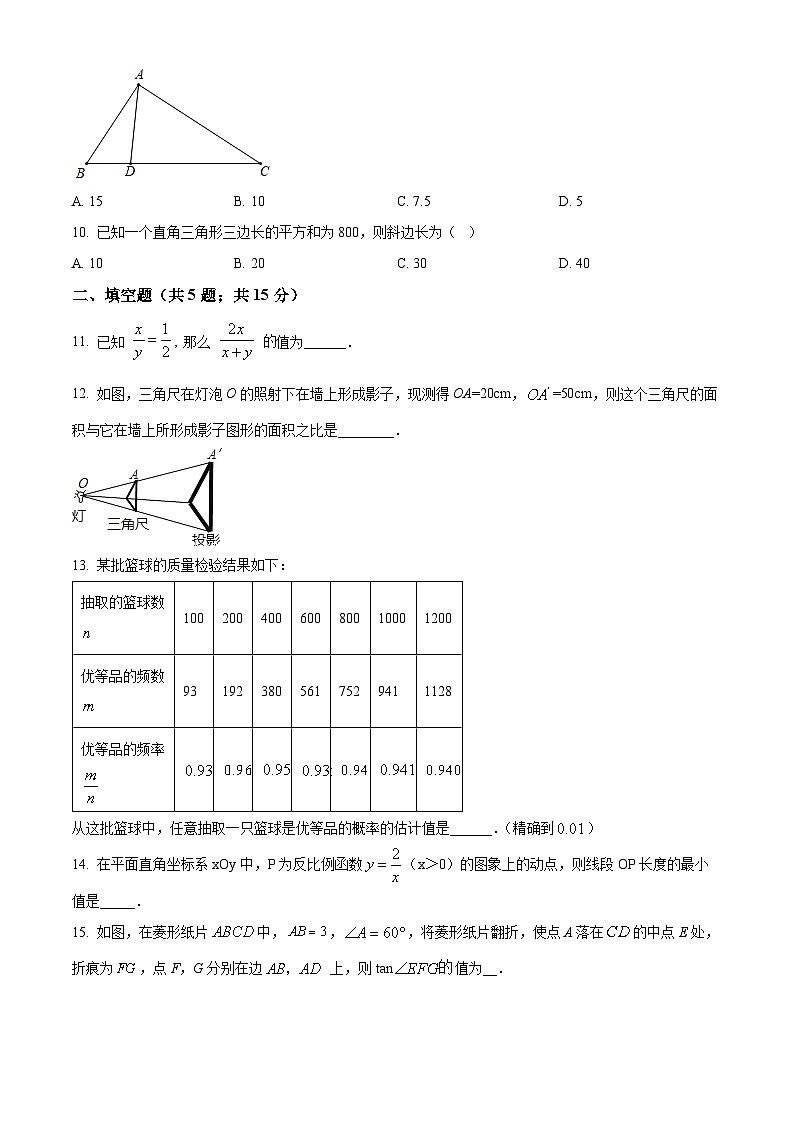
故选：A．【点睛】此题考查了解一元二次方程的配方法，熟练掌握完全平方公式是解本题的关键．6. 如图，在△ABC中，点D，E分别在AB，AC上，且DE∥BC，AD=1，BD=2，那么的值为（　　）A. 1：2 B. 1：3 C. 1：4 D. 2：3【答案】B【解析】【分析】由DE∥BC判定△ADE∽△ABC，得出比例式，进一步求得答案即可．【详解】∵DE∥BC，∴△ADE∽△ABC，∴=．∵AD=1，DB=2，∴=，∴=．故选B．【点睛】本题考查了相似三角形的判定与性质，掌握三角形的判定方法是解答本题的关键．7. 下列判断中错误的是（ ）A. 平行四边形的对边平行且相等．B. 四条边都相等且四个角也都相等四边形是正方形．C. 对角线互相垂直的四边形是菱形．D. 对角线相等的平行四边形是矩形．【答案】C【解析】【分析】根据平行四边形的性质、特殊四边形的判定即可作出判断．【详解】解：对角线互相垂直平分的四边形是菱形，即选项C错误，其余三个选项都正确，不符合题意．故选：C．【点睛】本题考查了平行四边形的性质、特殊平行四边形的判定，掌握这些判定与性质是解题的关键．8. 已知一次函数与反比例函数，在同一平面直角坐标系中的图象如图所示，则当时，的取值范围是（    ）A. 或 B. 或C. 或 D. 【答案】B【解析】【分析】根据题意可得，不等式的解集对应着反比例函数大于一次函数的部分，观察图像求解即可．【详解】解：由可得，即不等式的解集对应着反比例函数大于一次函数的部分，观察函数图像可得，当或，当时，的取值范围是或故选：B【点睛】此题考查了一次函数与反比例函数的结合问题，解题的关键是掌握函数的有关性质，利用数形结合的思想求解问题．9. 如图，点D是△ABC的边BC上一点，∠BAD＝∠C，AC＝2AD，如果△ACD的面积为15，那么△ABD的面积为（　　）A. 15 B. 10 C. 7.5 D. 5【答案】D【解析】【分析】首先证明△BAD∽△BCA，由相似三角形的性质可得：△BAD的面积：△BCA的面积为1：4，得出△BAD的面积：△ACD的面积＝1：3，即可求出△ABD的面积．【详解】解：∵∠BAD＝∠C，∠B＝∠B，∴△BAD∽△BCA，∵AC＝2AD，∴，∴，∵△ACD的面积为15，∴△ABD的面积＝×15＝5，故选：D．【点睛】本题主要考查了相似三角形的判定与性质，掌握相似三角形的判定与性质是解题的关键.10. 已知一个直角三角形三边长的平方和为800，则斜边长为（  ）A. 10 B. 20 C. 30 D. 40【答案】B【解析】【分析】设出直角三角形的两直角边分别为a，b，斜边为c，利用勾股定理得a2+b2=c2，，再由三边的平方和为800，得a2+b2+c2=800，根据两式即可求出斜边的长．【详解】解：设直角三角形的两直角边分别为a，b，斜边为c，
根据勾股定理得：a2+b2=c2，
∵a2+b2+c2=800，∴2c2=800，
∴c2=400，∴c=20（舍去负值）
故选：B．【点睛】此题考查了勾股定理，熟练掌握勾股定理a2+b2=c2是解题的关键．二、填空题（共5题；共15分）11. 已知 , 那么 的值为______．【答案】【解析】【分析】根据比例的性质求得，代入代数式求值即可详解】解：∵∴∴故答案为：【点睛】本题考查了比例的性质，掌握比例的性质是解题的关键．12. 如图，三角尺在灯泡O的照射下在墙上形成影子，现测得OA=20cm，=50cm，则这个三角尺的面积与它在墙上所形成影子图形的面积之比是________．【答案】4∶25##【解析】【详解】∵，∴三角尺的面积与它在墙上形成的影子的面积的比=．故答案为∶ 4∶25．13. 某批篮球的质量检验结果如下：抽取的篮球数10020040060080010001200优等品的频数931923805617529411128优等品的频率从这批篮球中，任意抽取一只篮球是优等品的概率的估计值是______．（精确到）【答案】0.94【解析】【分析】由表中数据可判断频率在0.94左右摆动，于是利于频率估计概率可判断任意抽取一只篮球是优等品的概率为0.94．【详解】解：从这批篮球中，任意抽取一只篮球是优等品的概率的估计值是0.94．故答案为：0.94．【点睛】本题考查了利用频率估计概率，首先通过实验得到事件的频率，然后用频率估计概率即可解决问题．14. 在平面直角坐标系xOy中，P为反比例函数（x＞0）的图象上的动点，则线段OP长度的最小值是_____．【答案】2【解析】【详解】根据题意可得：当P为直线y=x与反比例函数（x＞0）的交点时则线段OP长度的最小，由得：或（舍去），则P点的坐标为（，），则线段OP==2，故答案为2．15. 如图，在菱形纸片中，，，将菱形纸片翻折，使点A落在的中点E处，折痕为，点F，G分别在边 上，则tan值为__．【答案】##【解析】【分析】如图，连接交于O，连接，则为等边三角形，根据等腰三角形的三线合一得出，中，根据锐角函数的定义由，，分别得出CE，BE的长，中，利用勾股定理得出AE的长，根据折叠的性质得出，，设，则，中利用勾股定理建立方程，求解得出EF的长，中，利用勾股定理算出的长，根据正切函数的定义即可得出答案．【详解】解：如图，连接交于O，连接在菱形纸片中，，∴为等边三角形，∴，，∵E是的中点，∴，又∵，∴，∴在中， ，∴中， = ，由折叠可得，， = ，设，则，∵中，，∴，解得x= ，即 ，∴中， ，∴= ．故答案为： ．【点睛】本题考查了菱形的性质，等边三角形的判定与性质，解直角三角形，折叠的性质，勾股定理等知识，根据菱形的性质和等边三角形的性质得到和是直角三角形，由折叠的性质得到是直角三角形是解答本题的关键．三、解答题（共7题；共55分）16. 解方程：（1）；（2）．【答案】（1），；    （2），．【解析】【分析】（1）利用配方法求解即可；（2）移项后，利用因式分解法求解即可．【小问1详解】解：，，，，∴，；【小问2详解】解：，，或，∴，．【点睛】本题考查了解一元二次方程，能够根据方程特点灵活选用不同的解法是解题的关键．17. 先化简，再求值：，其中【答案】，【解析】【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，将x的值代入计算即可求出值．【详解】原式当时，原式【点睛】本题考查了分式化简求值以及运用特殊角三角函数值计算，解答此题的关键是把分式化到最简．18. 现有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字0，1，2；乙袋中装有3个完全相同的小球，分别标有数字，，0，现从甲袋中随机抽取一个小球，记录标有的数字为，再从乙袋中随机抽取一个小球，记录标有的数字为，确定点坐标为，求点在函数的图象上的概率．（用树状图法或列表法表示）【答案】【解析】【分析】画树状图，共有9个等可能的结果，点在函数的图象上的结果有2个，再由概率公式求解即可．【详解】解：画树状图如图：共有9个等可能的结果，点在函数的图象上的结果有(1，0)，(2，-1)共2个，∴点在函数的图象上的概率为．【点睛】本题考查了用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回试验还是不放回试验．用到的知识点为：概率=所求情况数与总情况数之比．19. 如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．（1）求证：四边形AECD是菱形；（2）如果点E是AB的中点，AC=4，EC=2.5，求四边形ABCD的面积．【答案】（1）证明见解析；（2）9【解析】【分析】（1）根据AB∥CD，CE∥AD得出平行四边形，根据角平分线的性质和平行线的性质得出∠DAC=∠ACD，从而说明AD=CD，得出菱形；（2）根据菱形的性质得出∠EAC=∠ACE，根据点E为中点得出∠B=∠ECB，从而得出∠ACB=90°，根据点E为中点得出EC=2.5，AB=5，BC=3，从而得出△ABC的面积，根据菱形的性质得出四边形的面积．【详解】（1）∵AB∥CD，CE∥AD，∴四边形AECD是平行四边形，∵AC平分∠BAD，∴，∵AB∥CD，∴，∴，∴AD=CD，∴四边形AECD是菱形．（2）∵四边形AECD是菱形，∴AE=CE，∴，∵点E是AB的中点，∴AE=BE，∴，∴，即∵点E是AB的中点，EC=2.5，∴AB=2EC=5，∴BC==3．∴S△ABC=． ∵点E是AB的中点，四边形AECD是菱形，∴S△AEC=S△EBC=S△ACD=3．∴四边形ABCD的面积=S△AEC+S△EBC+S△ACD=920. 阅读下面材料，并完成问题．任意给定一个矩形A，若存在另一个矩形B，使它的周长和面积分别是矩形A的一半，则称矩形是“兄弟矩形”．探究：当矩形A的边长分别为7和1时，是否存在A的“兄弟矩形”B？小亮同学是这样探究的：设所求矩形的两边分别是x和y，由题意，得由①，得，③把③代入②，得，整理，得．，的“兄弟矩形”B存在．（1）若已知矩形A的边长分别为3和2，请你根据小亮的探究方法，说明A的“兄弟矩形”B是否存在？（2）若矩形A的边长为m和n，当A的“兄弟矩形”B存在时，求应满足的条件．【答案】（1）不存在；（2）【解析】【分析】（1）按照小亮的方法，进行计算即可；（2）先根据小亮的方法列出方程组，转化为一元二次方程，利用根的判别式列不等式即可．【详解】解：（1）设所求矩形的两边分别是x和y，由题意，得由①，得，③把③代入②，得，整理，得，，的“兄弟矩形”B不存在．（2）设所求矩形的两边分别是x和y，由题意，得由①，得，③把③代入②，得，整理，得，，又都是正数，当时，A的“兄弟矩形”B存在．【点睛】本题考查了一元二次方程应用以及根的判别式，解题的关键是熟练运用一元二次方程根的判别式．21. 已知在中，，过点引一条射线，是上一点．【问题解决】（1）如图1，若，射线在内部，，求证：．小明同学展示的做法是：在上取一点使得，通过已知的条件，从而求得的度数，请你帮助小明写出证明过程；【类比探究】（2）如图2，已知．①当射线在内，求的度数；②当射线在下方，如图3所示，请问的度数会变化吗？若不变，请说明理由，若改变，请求出的度数【答案】（1）见解析；（2）①120°；②会变，60°【解析】【分析】（1）在上取一点使得，可证≌，求出∠ADC的度数，减去∠ADB的度数即可；（2）在上取一点，使得，可证≌，求出∠ADC的度数，减去∠ADB的度数即可；（3）在延长线上取一点，使得，按照（2）的方法可求．【详解】证明：（1）在上取一点使得，∵，∴为等边三角形，∵∴为等边三角形，∴，∴≌（）， ∴，∴；（2）①如图2，在上取一点，使得，∵，且，∴，∴，∴∴≌（），∴，∴， ②会变，如图3，在延长线上取一点，使得同理可得：≌（），∴， ∴．【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质，解题关键是恰当的作辅助线，构造“手拉手”手拉手全等模型，利用全等三角形的性质求角．22. 如图1，在平面直角坐标系中，抛物线y＝－＋x＋与x轴交于A、B两点(点A在点B的左侧)，与y轴交于点C，对称轴与x轴交于点D．（1）求直线BC的解析式；（2）如图2，点P为直线BC上方抛物线上一点，连接PB、PC．当的面积最大时，在线段BC上找一点E(不与B、C重合)，使BE的值最小，求点P的坐标和BE的最小值；（3）如图3，点G是线段CB的中点，将抛物线y＝－＋x＋沿x轴正方向平移得到新抛物线，y′经过点D，的顶点为F．在抛物线的对称轴上，是否存在一点Q，使得为直角三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由．【答案】（1）直线BC的解析式为y=﹣x+；（2）最大时，P(，)，PE+BE值最小，理由见解析；（3）存在，Q(3，），(3，−)，理由见解析．【解析】【分析】（1）根据二次函数的解析式先求出点C、点B的坐标，然后利用待定系数法即可求出直线BC的解析式；（2）如图2中，过点P作轴于点M，交直线BC于点F，过点E作轴于点N，设P(a，﹣+a+)，则F(a，﹣a+)则可得 PF=﹣+a，继而得S△PBC=﹣ +a，根据二次函数的性质可得当a=时，S△PBC最大，可得点P坐标，由直线BC的解析式为y=﹣x+可得，继而可得，根据两点之间线段最短和垂线段最短，则当P，E，N三点共线且垂直于x轴时，PE+BE值最小，据此即可求得答案；（3）由题意可得D(1，0)，G(，)，继而可得直线DG解析式，根据抛物线y=﹣ +x+=﹣+沿x轴正方向平移得到新抛物线，经过点D，可得═﹣+，从而可得对称轴为x=1，然后分或，三种情况进行讨论即可得.【详解】（1）当x=0时，y=﹣+x+=，∴点C的坐标为（0，）；当y=0时，有﹣+x+=0，解得：，∴点B的坐标为（3，0），设直线BC的解析式为，将B（3，0）、C（0，）代入，得：，解得：，∴直线BC的解析式为y=﹣x+；（2）如图2中，过点P作轴于点M，交直线BC于点F，过点E作轴于点N，设P（a，﹣+a+），则F（a，﹣a+），∴PF=﹣+a，∴S△PBC=×PF×3=﹣ +a，∴当a=时，S△PBC最大，∴P（，），∵直线BC的解析式为y=﹣x+，∴，轴，∴EN=BE，∴PE+BE=PE+EN，∴根据两点之间线段最短和垂线段最短，则当P，E，N三点共线且垂直于x轴时，PE+BE值最小，∴PE+BE=PE+EN=PN=；（3）∵D是对称轴直线x=1与x轴的交点，G是BC的中点，∴D（1，0），G（，），∴直线DG解析式y=x﹣，∵抛物线y=﹣+x+=﹣+沿x轴正方向平移得到新抛物线，经过点D(1,0)，∴═﹣+，∴对称轴为x=3，F(3, )∵为直角三角形，∴或，（不合题意，舍去）当，则轴∴Q（3，）当，设点Q坐标（3，y）∵．∴∴y＝−∴Q（3，−）综上所述：Q（3，），（3，−）．【点睛】本题考查了二次函数的综合题，涉及了待定系数法、二次函数的最值、二次函数图象的平移等，综合性较强，有一定的难度，正确添加辅助线、熟练掌握和应用相关知识是解题的关键．