人教版五年级数学上册第三单元表集体备课教案

这是一份人教版五年级数学上册第三单元表集体备课教案，文件包含第三单元例4到例8doc、例9和例10doc、例1doc、例2例3doc等4份教案配套教学资源，其中教案共36页， 欢迎下载使用。
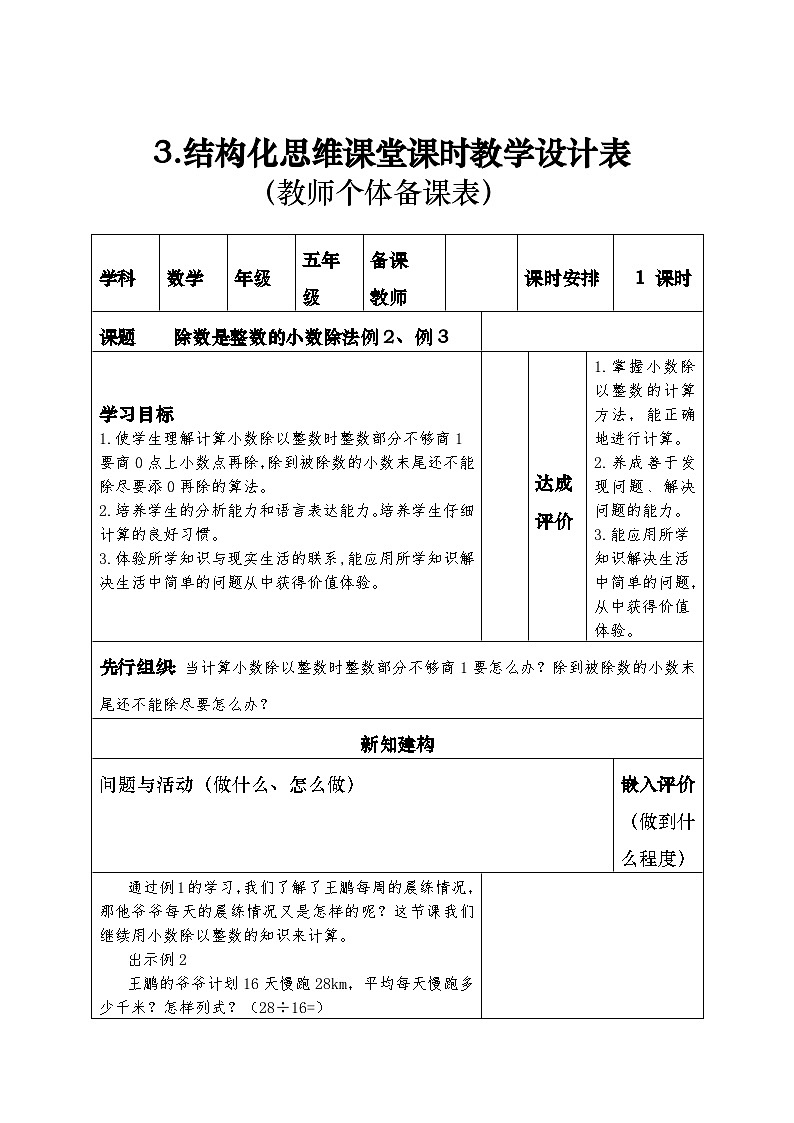
 学科数学年级五年级备课教师 课时安排 1 课时课题    一个数除以小数的小数除法例4 学习目标1.使学生理解并掌握除数是小数的除法计算法则，能正确地进行计算。2.初步掌握将除数是小数的除法转化为除数是整数的除法的推导过程，培养学生转化的数学思想。 达成评价1.借助商不变的规律把一个数除以小数转化为除数是整数的除法。2.掌握一个数除以小数的计算方法，做到“一看、二移、三算”，并能正确地进行计算。3.养成善于总结归纳的能力。 先行组织：当除数不是整数时，怎样计算？新知建构问题与活动（做什么、怎么做） 嵌入评价（做到什么程度） 任务一：说一说你是根据什么算出来的？（商不变的规律）什么叫商不变的规律？导入课题。这节课我们就来学习运用商不变的规律计算一个数除以小数的除法。（出示课题）    出示例4：奶奶编“中国结”，编一个要用0.85米丝绳。用7.65米丝绳可以编几个“中国结”？列式为7.65÷0.85＝任务二：（1）这个除法和我们学过的除法有什么不同？（引导学生回答，以前学习的除数是整数，这道题的除数是小数。）（2）如果能把这个除法转化成除数是整数的除法，我们就会算了。能不能把它转化成一个数除以整数的除法呢？如果能，该怎样转化？转化后应该怎样计算呢？学生交流汇报。方法一：把题中的米改成厘米。0.85米=85厘米7.65米=765厘米     方法二：根据商不变的规律，把被除数和除数同时扩大100倍。师：这两种方法都很不错，下面我们重点要研究第二种方法。提问：（1）为什么要把除数和被除数都扩大到原来的100倍呢？（引导学生说出把除数扩大到原来的100倍后，除数就变成了整数，为了使商不变，被除数也要扩大到原来的100倍。）（2）这样转化，竖式该怎样写？根据学生的回答，教师把7.65÷0.85写成竖式，边写转化过程边讲解，并用虚线框起来。   提问：把小数0.85扩大到它的100倍，就是把小数点向什么方向移动几位？（向右移动两位）教师重新写出7.65÷0.85的竖式，边复述讲解边示范把除数和被除数的小数点及没有用的“0”划去。   （3）归纳小结。师：通过刚才的学习，想一想：一个数除以小数，可以先怎样？再怎样？小结：先把除数扩大成整数，除数的小数点向右移动几位，被除数的小数点也向右移动几位，然后再按整数除法的法则进行计算。      式子很轻松的就能列得出来就是求7.65里面有几个0.85用除法计算。也能够知道如果除到被除数的末尾仍有余数，就在余数后面添0再继续除，直到除尽为止。                     能够联系以前学过的商中间和末尾有零除法。得到的商是不够1的小数，因而要在整数部分写“0”占位。点上小数点后再除。 迁移运用：先说说下面各题的除数和被除数需要同时扩大到原来的多少倍，怎样移动小数点，再计算62.4÷2.6       2.38÷0.34      0.544÷0.16成果集成：       一个数除以小数（1） 作业设计： 1.计算下面各题。5.04÷0.28  0.54÷0.18  2.25÷0.452.一块长方形菜地的面积是109.02平方米，它的宽是6.9米，长是多少米？             学科数学年级五年级备课教师 课时安排 1 课时课题    一个数除以小数的小数除法例5 学习目标1.掌握被除数和除数的小数位数不同的情况的计算方法，进一步探究一个数除以小数的计算方法，理解算理，总结计算法则。 2.培养学生利用旧知识解决新问题的能力。 3.培养学生转化矛盾、解决问题的能力。   达成评价1.在观察、交流、分析、对比、归纳中，体会转化的数学思想，发展运算的能力。2.养成善于发现问题、解决问题的能力。3.在解决实际问题中体会你数学的价值，养成乐于反思的学习习惯。先行组织：当被除数的小数位数比除数的小数位数少的时候该怎么办新知建构问题与活动（做什么、怎么做） 嵌入评价（做到什么程度）我们上节课已经对一个数除以小数的计算有了一定的了解，那老师现在就来考考大家。根据商不变的性质填空，并说明理由。4.68÷1.2=(    )÷12  2.38÷0.34=(    )÷(    )5.2÷0.32=(    )÷32   161÷0.46=(    )÷(    )任务一：用喜欢的方法计算12.6÷0.28=，把你的想法记录下来。1.学习例5。出示例5：12.6÷0.28=学生尝试计算，发现问题。提问：想一想这道题该怎样计算？有什么问题？学生汇报遇到的问题：被除数只有一位小数，除数有两位小数，把被除数12.6和除数0.28同时扩大到100倍时，被除数12.6的位数不够。小组讨论：当被除数的位数不够时怎么办呢？（在末尾补上“0”）补几个“0”？根据什么来确定补“0”的个数？引导总结：被除数中只有一位小数，除数中有两位小数，要想把除数变为整数，就要把被除数和除数中的小数点都向右移动两位，也就是使其同时扩大到原来的100倍。如果原来小数位数不够时，要在末尾用0补足。所以除数的小数点向右移动了几位，被除数中的小数点也要相应的向右移动几位，位数不够时，少几位就补几个。学生按照上面讨论的方法重新计算12.6÷0.28。指名学生说说计算过程和方法，教师边复述边板演。     任务一：把下面的算式转化成除数是整数的除法算式。（1）6.3 ÷ 0.03=（ ）÷ 3  （2）5.58÷ 3.1=（ ） ÷（ ）   （3）8.4 ÷ 3.5=（ ）÷35       （4）161÷  0.46=（ ） ÷ （ ）2.即时巩固。完成课本第29页“做一做”第2题。3.总结：小数除法的计算方法。小结：小数除法的计算方法和步骤：一看：看清除数有几位小数；二移：把除数和被除数的小数点同时向右移动相同的位数，使除数变成整数。当被除数位数不足时，用“0”补足；三算：按照除数是整数的小数除法的方法计算。4.典例讲析。计算0.19÷0.03，当商是6时，余数是多少？方法一分析：这是一道除数是小数的除法题，计算时把它转化为除数是整数的除法计算。转化时，被除数0.19和除数0.03要同时扩大到原来的100倍。根据商不变的性质，可知此时商的大小不变，但余数要同时扩大到原来的100倍。因此，要把竖式中所得余数再缩小到原来的，就能求出原式的余数。解：0.19÷0.03=6……0.01  余数是0.01。方法二分析：在有余数的除法中，“余数=被除数-商×除数”。已知被除数是0.19，除数是0.03，商是6,根据上述数量关系可以求出余数。解：6×0.03=0.180.19-0.18=0.01总结：1.在除法中，被除数和除数同时扩大到原来的10倍、100倍……商的大小不变，但是余数也随着扩大到原来的10倍、100倍……要求原余数，就是求新余数（即竖式中余数）的110、1100……2.求小数除法算式中的余数，也可以用被除数减去商与除数的乘积。  分析：这是一道小数除法题，按照小数除法的计算方法计算。除数中有14位小数，应把被除数和除数的小数点同时向右移动14位，而被除数中只有13位小数，被除数的小数位数不够，用“0”补位，原式就转化为6250÷25。  【课堂作业】1.完成教材第29页“做一做”中第1题。分四组做，每组2道小题，4名同学板演，2名同学讲算理。2.完成教材第30页练习七第5题。独立完成后交流。【课堂小结】提问：通过这节课的学习，你有哪些收获？小结：计算被除数的小数位数比除数的小数位数少的小数除法时，同时将被除数与除数的小数点向右移动相同的位数，被除数的小数位数不够，少几位就在被除数末尾补几个“0”。     把除数是小数的除法转化成除数是整数的除法时，小数点向右移动的位数由除数来决定。除数移动几位，被除数也要移动几位。                     根据商不变的性质，掌握“一看”、“二移”、“三算”的计算算理。 迁移运用：小马虎在计算一个数除7.2时，把商的小数点向左点错了一位，结果是0.24，原除法算式中的除数是多少？成果集成：       一个数除以小数（2）例5：12.6÷0.28=   小数除法的计算方法和步骤：一看：看清除数有几位小数；二移：把除数和被除数的小数点同时向右移动相〗同的位数，使除数变成整数。当被除数位数不足时，用“0”补足；三算：按照除数是整数的小数除法的方法计算。  作业设计：1.根据5406÷53=102,直接写出下面各题的商。     (1)540.6÷5.3=　　(2)54.06÷0.53=　　(3)5.406÷0.053=　　(4)54060÷530= 2.判断下列各式得数是否相等,说明为什么。       (1)5.04÷0.6与50.4÷6　　　　　　(2)0.84÷0.28与84÷28        (3)319.4÷0.05与3194÷5         (4)0.224÷0.04与224÷43.下面的计算对吗?如果不对,错在哪儿?        学科数学年级五年级备课教师 课时安排 1 课时课题    求商的近似数例6 学习目标1.能理解商的近似数的意义。     2.掌握小数除法计算中用“四舍五入”法求商的近似数的一般方法。    3.培养学生在实际生活中灵活运用数学知识的能力，能根据实际情况进行求近似数。  达成评价1.能结合实际情况用“进一”法或“去尾”法取商的近似数。2.培养学生的实践能力和思维的灵活性，培养学生解决实际问题的能力。3.引导学生根据生活中的实际情况多角度思考问题，灵活地取商的近似数先行组织：当计算小数除法，除得的位数相当多时，我们要求商的近似数，知道四舍五入法新知建构问题与活动（做什么、怎么做） 嵌入评价（做到什么程度）1.学习例6。出示例6情境图，观察图，弄清题意。爸爸给王鹏新买了1打（12个）羽毛球，一共用了19.4元，1个大约多少钱？任务一：尝试解决问题，可以写一写、算一算，求出每个羽毛球大约多少钱？把思考的过程记录下来。师生共同分析：列式：19.4÷12当学生除不尽时，组织讨论：（1）你遇到了什么问题？（除不尽）你除出来的结果是多少？板书：19.4÷12=1.6166666…（2）那一个羽毛球的价钱到底是多少呢？这个1.6166666…到底是多少钱？是不是我们就没办法定出一个羽毛球的价钱呢？你们准备怎么给这一个羽毛球定价，为什么？学生小组讨论，教师巡视，听取学生的意见。讨论结束后，各小组成员发表意见。意见1：羽毛球的定价是1.6元。因为1.6元比较接近1.616666…元。意见2：羽毛球的定价是1.61元。因为货币最小面值是“分”，把“分”后面那些“6”去掉了就行。意见3：羽毛球的定价是1.62元。因为1.616666…用“四舍五入”法保留到“分”，也就是保留两位小数是1.62。意见4：羽毛球的定价是2元。因为这样比较方便给钱，保留整数就好了。师：同学们都想得不错，这么多定价，你觉得哪个更合适？为什么？小结：定价1.62最接近准确价格，最合适。 任务一：尝试解决问题后，根据要求试做下面的题，并把思考的过程记录下来。 2.探究求商的技巧。出示探究题：计算48÷23（得数保留两位小数）学生尝试练习，教师巡视指导。学生汇报，展示几个同学的计算结果及过程。提问：你认为哪种算法比较简便？为什么？小结：第二种方法比较简便，因为保留两位小数只要计算到第三位小数就够了。提问：如果把题目改改，要求保留一位小数，保留三位小数，保留九位小数呢？谁能用一句话概括出你的发现？总结：求商的近似数时，计算出的数中的小数位数要比要求保留的小数位数多一位。3.即时巩固。                                             课本第32页“做一做”。请3名同学板演，让板演的同学说一说是怎样做的。4.与积的近似数的求法进行比较。结合例题与复习题，比较求商的近似数和求积的近似数的异同点。独立思考后小组交流。学生充分发表意见后，教师综合学生的发言总结出求商的近似数和求积的近似数的异同点：相同点：都按照“四舍五入”法取近似数。不同点：取商的近似数只要计算时比要保留的小数位数多除出一位就可以了；而取积的近似数时则要计算出整个积的数以后再取近似数。5.典例讲析。用7、3、9、0和小数点组成不同的小数，其中哪些小数四舍五入后的近似值为4？哪些小数四舍五入后的近似值小于1？分析：由题意可知：（1）近似值为4的小数，其整数部分一定为3，且要经过“五入”方可取值为4，所以该小数的十分位可能是7，也可能是9。（2）近似值小于1的小数，0必须放在整数部分，且要经过“四舍”后方可取值为0（0＜1），所以该小数的十分位不可能是7或9，只能是3。解：近似值为4的小数有3.790,3.709，3.907，3.970。近似值小于1的小数有：0.379，0.397。总结：已知近似数，确定准确数的取值范围，一定要看准近似数是精确到哪一位，准确数必须要考虑该数位下一位上的数字。      “大约”说明算式可能除不尽或商的小数位数过多，商要用四舍五入法保留一定的小数位数。                               求商的近似数时，先看要求保留几位小数，再计算到比保留的小数位数多一位，然后将最后一位上的数字“四舍五入”。 迁移运用：一支铺路队铺一段公路。上午工作3.5小时，铺了164.9米；下午工作4.5小时，铺了206.7米。这支铺路队是上午铺得快还是下午铺得快？成果集成：       商的近似数例7：19.4÷12= ＿＿＿（元） 作业设计：按计算下面各题。（1）得数保留一位小数48÷2.3     1.55÷3.8   7.09÷0.52（2）得数保留两位小数3.81÷7   246.4÷13   5.63÷6.12.数学书第37页第8题       学科数学年级五年级备课教师 课时安排 1 课时课题    循环小数   例7、例8 学习目标1.通过求商，使学生感受到循环小数的特点，从而理解循环小数的概念，了解循环小数的简便记法。2.理解有限小数，无限小数的意义，扩展数的范围。3.培养学生抽象概括能力，及敢于质疑和独立思考的习惯 达成评价1.能理解“有限小数”和“无限小数”的意义。通过求商，使学生感受到循环小数的特点，从而理解循环小数的概念，了解循环小数的简便记法。2.培养学生发现问题、提出问题、解决问题的能力，提高其观察、分析、比较、判断、抽象和概括的能力。先行组织：当计算小数除以整数时整数部分不够商1要怎么办？除到被除数的小数末尾还不能除尽要怎么办？新知建构问题与活动（做什么、怎么做） 嵌入评价（做到什么程度）师：同学们，我给你们讲一个故事，欢迎吗？好，那你们可要认真听哟！从前有座山，山上有座庙，庙里有两个和尚，有一天，大和尚给小和尚讲故事：从前有座山，山上有座庙，庙里有两个和尚，有一天，大和尚给小和尚讲故事：从前有座山，山上有座庙，庙里有两个和尚……师：同学们，老师的故事讲得好吗？你发现了什么？（讲得不太好，在重复同一个内容）谁能根据这个故事的特点继续往下讲。让几个学生继续讲这个重复的故事。提问：像这样重复下去，这个故事讲得完吗？（永远讲不完）这种不断重复的现象你还在生活中哪些地方见过？学生汇报。（1）一个星期七天重复出现。（2）太阳东升西落。（3）一年四季交替出现。  ……师：大家很善于举一反三，生活中像这种“不断重复出现”的现象有很多，我们把这种“依次不断重复出现”的现象还可以叫做“循环现象”。你能用我们学习过的词语描述一下这种现象吗？学生汇报：周而复始，日复一日，潮起潮落，冬去春来……师：生活中有很多循环现象，数学中也有循环现象。这节课我们就来探究这个问题。【新课讲授】任务一：根据信息，列算式计算，并把思考的过程记录下来。1.学习例7。出示例7情境图。学生观察图，弄清图意后，列式：400÷75师：请同学们用竖式计算这个算式，看在计算过程中你有什么发现？发现：（1）余数重复出现“25”；（2）商的小数部分重复出现“3”；（3）继续除下去，永远除不完。老师带领学生验证       师：刚才我们发现了这个算式的三个特点，下面我们探讨一个问题：为什么商的小数部分总是重复出现“3”？它和每次出现的余数有什么关系？引导学生发现：当余数重复出现时，商就要重复出现；商是随着余数重复出现才重复出现的。师：猜想一下，如果继续除下去，商会是多少？（学生说出：如果继续除下去，只要余数出现25后，它的商也可以出现3。）我们怎样表示400÷75的商呢？（引导学生说出：可以用省略号来表示永远除不尽的商。）教师随学生板书：400÷75=5.333…讲解：我们所说的重复也叫做循环，像5.33…这样小数部分有一个数字依次不断地重复出现的小数，就是循环小数。任务二：先计算，再观察它们商的特点。看看你有什么发现？ 28÷18                78.6÷11学生独立计算，然后汇报展示。板书：78.6÷11=7.14545…       提问：比较这两个算式的商，也就是5.333…和7.14545…，你觉得这两个小数有什么不同？引导学生说出5.333…是从小数的第一位起不断重复出现数字“3”，而7.14545…是从小数第二位起开始不断的依次重复出现数字“4”和“5”。讨论：你觉得这样的算式除到哪一位就可以不除了？（引导学生说出：只要余数重复了，就可以不除了。）为什么？（引导学生说出：因为像这样的算式，余数循环，商也会跟着循环。）师：像5.333…和7.14545…这样的小数都是循环小数，你能写几个像这样的循环小数吗？观察这些小数，它们都有什么共同点？（引导学生说出：都是从小数部分的某一位起，都有一个数字或几个数字依次不断地重复出现。）任务三：阅读数学书34页的这部分内容，并把你认为重要的内容画下来。  3.学习简便记法，认识有限小数和无限小数。教师介绍：这些循环小数还可以用这样的方式来写：5.33…=5.、7.14545…=7.1,这就是用循环节表示循环小数。请阅读第34页材料。4.即时巩固师：请同学们计算15÷16和1.5÷7。学生计算后，教师提问：从中你发现了什么？讲解：像这样两个数相除，如果得不到整数商，所得到的商可能会有两种情况，你知道是哪两种吗？（引导学生说出：一种小数部分的位数是有限的，一种小数部分的位数是无限的。）教师介绍：小数部分的位数是有限的小数，叫做有限小数。小数部分的位数是无限的小数，叫做无限小数。循环小数属于无限小数。请同学们写几个有限小数，再写几个无限小数。【课堂作业】1.是循环小数的在（  ）里打“√”。3.5555…（ ）  2.50909(  )3.1415926…(  )  8.24626…(  )0.364364(  )   4.01230…(  )2.用简便方法表示下面的循环小数。0.4242…（  ）  2.737373…(  )1.61666…(  )  3.24572457…（  ）8.0060606…（  ） 7.144144…（  ）【课堂小结】提问：这节课你学习了什么新知识？你还有什么收获？小结：这节课我们学习了循环小数的特点，理解了循环小数的概念，掌握了循环小数的简便记法。                            在进行除法计算时，有些算式不但除不尽，而且余数不断重复出现，使得商中的某些数字也不断重复出现，此时商的小数部分是无限的，便产生了循环小数。                                              虽然除不尽，但是商是精确数，因此要用“=”连接。迁移运用：两个数相除，如果不能得到整数商，所得的商会有几种情况28÷16=1.75         400÷75=5.333…       4.48÷3.2=1.4       78.6÷11=7.14545… 成果集成：         循环小数       作业设计：用简便形式写出下面的循环小数1.555……    1.746746……    0.105353……计算下面各题，除不尽的先用循环小数表示所得的商，再保留两位小数。2.29÷1.1      153÷7.2    23÷3.3