





- 新教材2023_2024学年高中数学第5章函数应用2实际问题中的函数模型2.1实际问题的函数刻画2.2用函数模型解决实际问题分层作业课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第6章统计1获取数据的途径1.1直接获取与间接获取数据1.2普查和抽查1.3总体和样本分层作业课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第6章统计2抽样的基本方法2.1简单随机抽样分层作业课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第6章统计2抽样的基本方法2.2分层随机抽样分层作业课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第6章统计3用样本估计总体分布3.1从频数到频率3.2频率分布直方图分层作业课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第6章统计4用样本估计总体数字特征4.1样本的数字特征4.2分层随机抽样的均值与方差4.3百分位数分层作业课件北师大版必修第一册 课件 0 次下载
北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解作业课件ppt
展开1.已知函数f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在区间(1,2)上的近似解的过程中得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的解落在区间( )A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定
解析 ∵f(1)<0,f(1.5)>0,f(1.25)<0,∴f(1.25)·f(1.5)<0,因此方程的解落在区间(1.25,1.5)内,故选B.
2.(多选题)下列函数中,能用二分法求函数零点的有( )A.f(x)=3x-1B.f(x)=x2-4x+4C.f(x)=lg4xD.f(x)=ex-2
解析 f(x)=x2-4x+4=(x-2)2,f(2)=0,当x<2时,f(x)>0,当x>2时,f(x)>0,在零点两侧函数值同号,不能用二分法求零点,其余选项中在函数的零点两侧函数值异号.故选ACD.
3.若函数f(x)=x2-4x+m存在零点,且不能用二分法求该函数的零点,则m的取值范围是( )A.(4,+∞)B.(-∞,4)C.{4}D.[4,+∞)
解析 易知方程x2-4x+m=0有实数根,且Δ=16-4m=0,知m=4.
4.(多选题)某同学求函数f(x)=ln x+2x-6的零点时,用计算器算得部分函数值,如表所示:
则方程ln x+2x-6=0的近似解(精确度0.1)可取为( )
解析 由表格函数值在0的左右两侧,最接近的值,即f(2.5)≈-0.084,f(2.562 5) ≈0.066可知方程ln x+2x-6=0的近似根在(2.5,2.562 5)内,因此选项A中2.52符合,选项B中2.56也符合,故选AB.
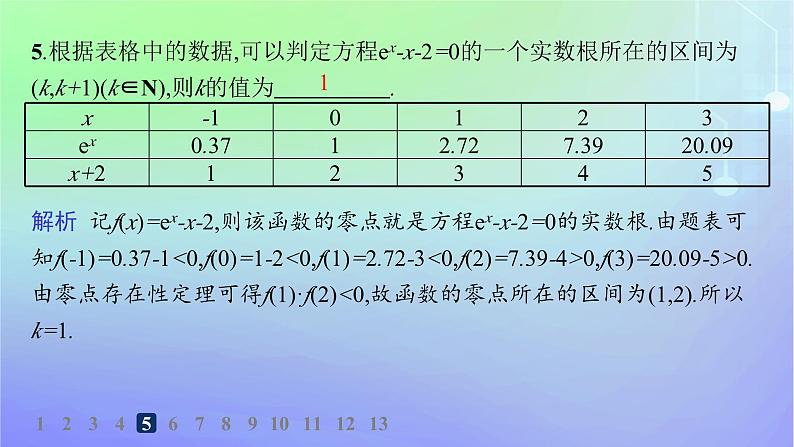
5.根据表格中的数据,可以判定方程ex-x-2=0的一个实数根所在的区间为(k,k+1)(k∈N),则k的值为 .
解析 记f(x)=ex-x-2,则该函数的零点就是方程ex-x-2=0的实数根.由题表可知f(-1)=0.37-1<0,f(0)=1-2<0,f(1)=2.72-3<0,f(2)=7.39-4>0,f(3)=20.09-5>0.由零点存在性定理可得f(1)·f(2)<0,故函数的零点所在的区间为(1,2).所以k=1.
6.一块电路板的线路AB之间有64个串联的焊接点(不含端点A,B),如果线路不通的原因是由于焊口脱落所致,要想检验出哪一处的焊口脱落,则至多需要检测 次.
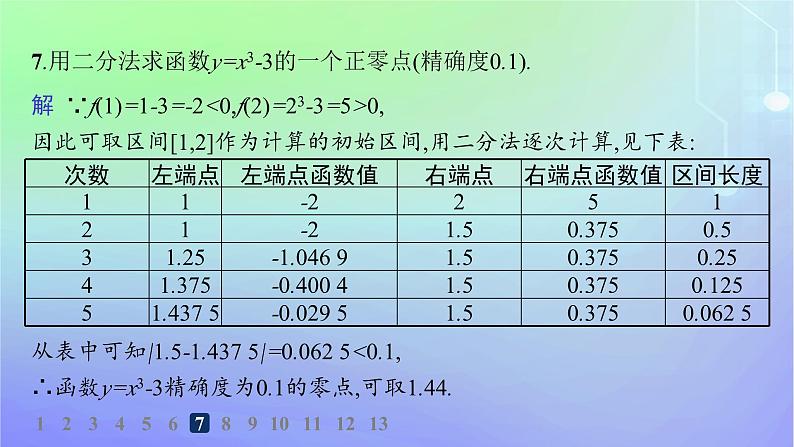
7.用二分法求函数y=x3-3的一个正零点(精确度0.1).
解 ∵f(1)=1-3=-2<0,f(2)=23-3=5>0,因此可取区间[1,2]作为计算的初始区间,用二分法逐次计算,见下表:
从表中可知|1.5-1.437 5|=0.062 5<0.1,∴函数y=x3-3精确度为0.1的零点,可取1.44.
解析 由二分法的步骤可知①零点在(0,4)内,则有f(0)·f(4)<0,不妨设f(0)>0,f(4)<0,取中点2;②零点在(0,2)内,则有f(0)·f(2)<0,则f(0)>0,f(2)<0,取中点1;③零点在(1,2)内,则有f(1)·f(2)<0,则f(1)>0,f(2)<0,取中点 ;
9.已知函数f(x)=2x- 在区间(1,2)上有一个零点x0,如果用二分法求x0的近似值(精确度为0.01),则应将区间(1,2)至少等分的次数为( )A.5B.6C.7D.8
10.求方程3x+ =0的近似解(精确度0.1).
g(x)与h(x)图象的交点的横坐标位于区间(-1,0),且只有一个交点,∴原方程只有一个解x=x0.
∵|-0.437 5-(-0.375)|=0.062 5<0.1,∴原方程的近似解可取为-0.437 5.
11.已知方程2x+2x=5.(1)判断该方程解的个数以及所在区间;(2)用二分法求出方程的近似解(精确度0.1).参考数值:
解 (1)令f(x)=2x+2x-5.因为函数f(x)=2x+2x-5在R上是增函数,所以函数f(x)=2x+2x-5至多有一个零点.因为f(1)=21+2×1-5=-1<0,f(2)=22+2×2-5=3>0,所以函数f(x)=2x+2x-5的零点在(1,2)内.
(2)用二分法逐次计算,列表如下:
因为|1.375-1.25|=0.125>0.1,且|1.312 5-1.25|=0.062 5<0.1,所以函数的零点近似值可取1.312 5,即方程2x+2x=5的近似解为1.312 5.
12.某公司生产A种型号的电脑,2019年平均每台电脑的生产成本为5 000元,并按纯利润为20%定出厂价.2020年开始,公司更新设备,加强管理,逐步推行股份制,从而使生产成本逐年降低,2023年平均每台A种型号的电脑出厂价仅是2019年的80%,实现了纯利润50%.(1)求2023年每台A种型号电脑的生产成本;(2)以2019年的生产成本为基数,用二分法求2019~2023年间平均每年生产成本降低的百分率(精确度0.01).
解 (1)设2023年每台A种型号电脑的生产成本为p元,根据题意,得(1+50%)p=5 000×(1+20%)×80%,解得p=3 200.故2023年每台A种型号电脑的生产成本为3 200元.(2)设2019~2023年间平均每年生产成本降低的百分率为x(0
13.已知函数f(x)= x3-x2+1.(1)证明方程f(x)=0在区间(0,2)内有实数解;(2)请使用二分法,取区间的中点二次,指出方程f(x)=0,x∈[0,2]的实数解x0在哪个较小的区间内.
北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解课文ppt课件: 这是一份北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解课文ppt课件,共33页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。
必修 第一册1.2 利用二分法求方程的近似解教学ppt课件: 这是一份必修 第一册1.2 利用二分法求方程的近似解教学ppt课件,共21页。PPT课件主要包含了选定初始区间,取区间中点,得到新区间,课堂小结,谢谢大家等内容,欢迎下载使用。
北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解评课课件ppt: 这是一份北师大版 (2019)必修 第一册1.2 利用二分法求方程的近似解评课课件ppt,共40页。













