





还剩31页未读,
继续阅读
成套系列资料,整套一键下载
- 新教材2023_2024学年高中数学第1章预备知识4一元二次函数与一元二次不等式4.1一元二次函数课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第1章预备知识4一元二次函数与一元二次不等式4.2一元二次不等式及其解法4.3一元二次不等式的应用课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第2章函数1生活中的变量关系2函数2.1函数概念课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第2章函数1生活中的变量关系2函数2.2函数的表示法第1课时函数的表示法课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第2章函数3函数的单调性和最值第1课时函数的单调性课件北师大版必修第一册 课件 0 次下载
新教材2023_2024学年高中数学第1章预备知识本章总结提升课件北师大版必修第一册
展开
这是一份新教材2023_2024学年高中数学第1章预备知识本章总结提升课件北师大版必修第一册,共39页。
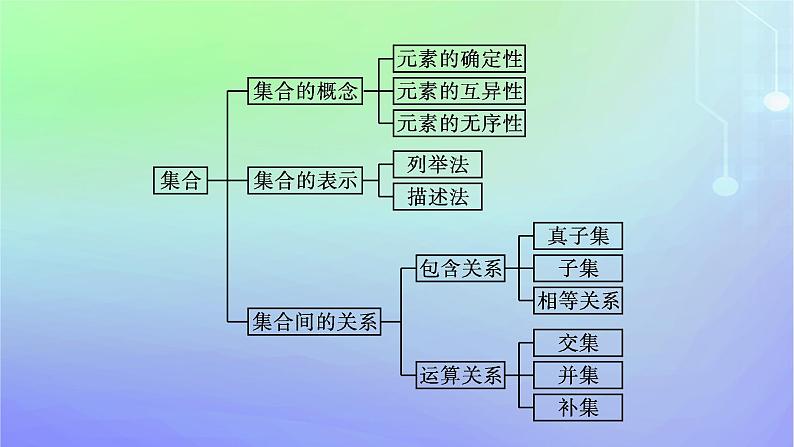
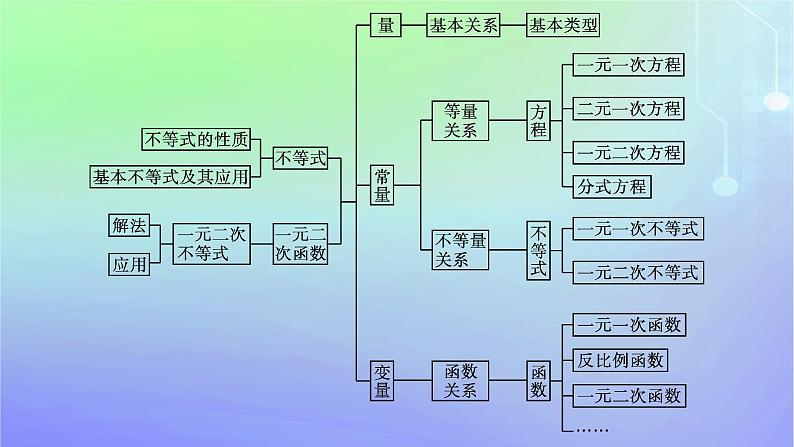
第一章本章总结提升网络构建·归纳整合专题突破·素养提升目录索引 网络构建·归纳整合专题突破·素养提升专题一 集合的综合运算1.集合的运算有交、并、补这三种常见的运算,它是集合中的核心内容.在进行集合的运算时,往往由于运算能力差或考虑不全面而出错,此时,数轴分析(或Venn图)是个好帮手,能将复杂问题直观化.在具体应用时要注意检验端点值是否适合题意,以免增解或漏解.2.掌握集合的基本关系与基本运算,重点提升逻辑推理和数学运算素养.【例1】 已知集合A={x|x>3a+1},B={x|x2-5x+6>0}.(1)当a=3时,求A∩B;(2)若A∪B=B,求实数a的取值范围.解 (1)当a=3时,集合A={x|x>10},集合B={x|x2-5x+6>0}={x|x<2,或x>3},所以A∩B={x|x>10}.(2)因为A∪B=B,所以A⊆B,所以3a+1≥3,解得所以实数a的取值范围为[ ,+∞).规律方法 集合运算过程中应力求做到“三化”(1)意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数自变量的取值范围、因变量的取值范围,还是表示方程或不等式的 解集.(2)具体化:具体求出相关集合中函数的自变量、因变量的取值范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.(3)直观化:借助数轴、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.变式训练1已知集合A={x|2≤x≤8},B={x|1a},U=R.(1)求A∪B,(∁UA)∩B;(2)若A∩C≠⌀,求a的取值范围.解 (1)A∪B={x|2≤x≤8}∪{x|18},∴(∁UA)∩B={x|15”是“A⊆B”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A 解析 A⊆B⇔a>4,而a>5⇒a>4,且a>4不能推出a>5,所以“a>5”是“A⊆B”的充分不必要条件.(2)设集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22},则“A=(A∩B)”的充要条件为 ;一个充分不必要条件可为 . a≤96≤a≤9(答案不唯一) 解析 A=(A∩B)⇔A⊆B,若A=⌀,则2a+1>3a-5,解得a<6;综上可知,“A=(A∩B)”的充要条件为a≤9;一个充分不必要条件可为6≤a≤9.专题三 全称量词命题与存在量词命题1.全称量词命题的否定一定是存在量词命题,存在量词命题的否定一定是全称量词命题.含有量词的命题否定时,首先改变量词,把全称量词改为存在量词,把存在量词改为全称量词,然后把判断词加以否定.2.通过含有量词的命题的否定及利用命题的真假求参数范围等,培养逻辑推理和数学运算素养.【例3】 (1)命题“∀x∈R,x2-2x+1≥0”的否定是( )A.∃x∈R,x2-2x+1≤0B.∃x∈R,x2-2x+1≥0C.∃x∈R,x2-2x+1<0D.∀x∈R,x2-2x+1<0C解析 ∵命题“∀x∈R,x2-2x+1≥0”为全称量词命题,∴命题的否定为:∃x∈R,x2-2x+1<0.故选C.(2)若命题p:∀x∈R,x2-2x+m≠0是真命题,则实数m的取值范围是( )A.[1,+∞) B.(1,+∞)C.(-∞,1) D.(-∞,1]B解析 命题p:∀x∈R,x2-2x+m≠0是真命题,则m≠-(x2-2x),∵-(x2-2x)=-(x-1)2+1≤1,∴m>1.故选B.规律方法 全称量词命题、存在量词命题真假的判断(1)全称量词命题的真假判定:要判定一个全称量词命题为真,必须对限定集合M中每一个x验证p(x)成立,一般用代数推理的方法加以证明;要判定一个全称量词命题为假,只需举出一个反例即可.(2)存在量词命题的真假判定:要判定一个存在量词命题为真,只要在限定集合M中,找到一个x,使p(x)成立即可;否则,这一存在量词命题为假.变式训练3(1)∃m,n∈Z,使得m2=n2+2 021成立的否定是( )A.∀m,n∈Z,有m2=n2+2 021B.∃m,n∈Z,使得m2≠n2+2 021成立C.∀m,n∈Z,有m2≠n2+2 021D.以上都不对C解析 存在量词命题的否定是全称量词命题. (2)设命题p:∀x∈R,x2+ax+2<0,若p的否定为真命题,则实数a的取值范围是 . R解析 p的否定:∃x∈R,x2+ax+2≥0为真命题,显然a∈R.专题四 基本不等式及应用1.基本不等式: (a≥0,b≥0)是每年高考的热点,主要考查实数比较大小、不等式证明以及求最值问题,特别是求最值问题往往与实际问题相结合,同时在基本不等式的使用条件上设置一些问题,实际上是考查学生恒等变形的技巧,另外,基本不等式的和与积的转化在高考中也经常出现.2.熟练掌握基本不等式的应用,重点提升数学抽象和数学运算素养.C6规律方法 (1)注意寻求已知条件与目标函数之间的联系.(2)利用添项和拆项的配凑方法,使积(或和)产生定值.特别注意“1”的代换.解 (1)由 =1,得b+a=ab,即ab-b-a+1=1,∴(a-1)(b-1)=ab-b-a+1=1.(2)由(1)得(a-1)(b-1)=1,专题五 解一元二次不等式1.对于不含参数的一元二次不等式首先转化为标准形式,然后能分解因式的变成因式相乘的形式,从而得到不等式的解集.2.对于含参数的不等式要注意对参数进行讨论,做到不重不漏.3.掌握不等式的解法,重点提升逻辑推理和数学运算素养.【例5】 解关于x的不等式x2-(a+a2)x+a3>0(a∈R). 解 原不等式可化为(x-a)(x-a2)>0.当a<0时,aa2};当a=0时,a2=a,原不等式的解集为{x|x≠0};当0a};当a=1时,a2=a,原不等式的解集为{x|x≠1};当a>1时,aa2}.综上所述,当a<0或a>1时,原不等式的解集为{x|xa2};当0a};当a=1时,原不等式的解集为{x|x≠1};当a=0时,原不等式的解集为{x|x≠0}.规律方法 对于含参数的一元二次不等式,若二次项系数为常数,则可先考虑分解因式,再对参数进行讨论;若不易分解因式,则可对判别式分类讨论,分类要不重不漏.变式训练5若一元二次不等式(1-a)·x2-4x+6>0的解集是{x|-3t,即t< 时,不等式的解集为{x|t 时,不等式的解集为{x|1-t
第一章本章总结提升网络构建·归纳整合专题突破·素养提升目录索引 网络构建·归纳整合专题突破·素养提升专题一 集合的综合运算1.集合的运算有交、并、补这三种常见的运算,它是集合中的核心内容.在进行集合的运算时,往往由于运算能力差或考虑不全面而出错,此时,数轴分析(或Venn图)是个好帮手,能将复杂问题直观化.在具体应用时要注意检验端点值是否适合题意,以免增解或漏解.2.掌握集合的基本关系与基本运算,重点提升逻辑推理和数学运算素养.【例1】 已知集合A={x|x>3a+1},B={x|x2-5x+6>0}.(1)当a=3时,求A∩B;(2)若A∪B=B,求实数a的取值范围.解 (1)当a=3时,集合A={x|x>10},集合B={x|x2-5x+6>0}={x|x<2,或x>3},所以A∩B={x|x>10}.(2)因为A∪B=B,所以A⊆B,所以3a+1≥3,解得所以实数a的取值范围为[ ,+∞).规律方法 集合运算过程中应力求做到“三化”(1)意义化:首先分清集合的类型,是表示数集、点集,还是某类图形;是表示函数自变量的取值范围、因变量的取值范围,还是表示方程或不等式的 解集.(2)具体化:具体求出相关集合中函数的自变量、因变量的取值范围或方程、不等式的解集等;不能具体求出的,也应力求将相关集合转化为最简形式.(3)直观化:借助数轴、Venn图等将有关集合直观地表示出来,从而借助数形结合思想解决问题.变式训练1已知集合A={x|2≤x≤8},B={x|1
相关资料
更多









