






还剩27页未读,
继续阅读
成套系列资料,整套一键下载
- 新教材2023_2024学年高中数学第6章统计4用样本估计总体数字特征4.1样本的数字特征4.2分层随机抽样的均值与方差4.3百分位数课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章概率1随机现象与随机事件1.1随机现象1.2样本空间1.3随机事件1.4随机事件的运算课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章概率2古典概型2.1古典概型2.2古典概型的应用第1课时古典概型的概率计算公式及其应用课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章概率2古典概型2.1古典概型2.2古典概型的应用第2课时互斥事件概率的求法课件北师大版必修第一册 课件 0 次下载
- 新教材2023_2024学年高中数学第7章概率3频率与概率课件北师大版必修第一册 课件 0 次下载
新教材2023_2024学年高中数学第6章统计本章总结提升课件北师大版必修第一册
展开
这是一份新教材2023_2024学年高中数学第6章统计本章总结提升课件北师大版必修第一册,共35页。
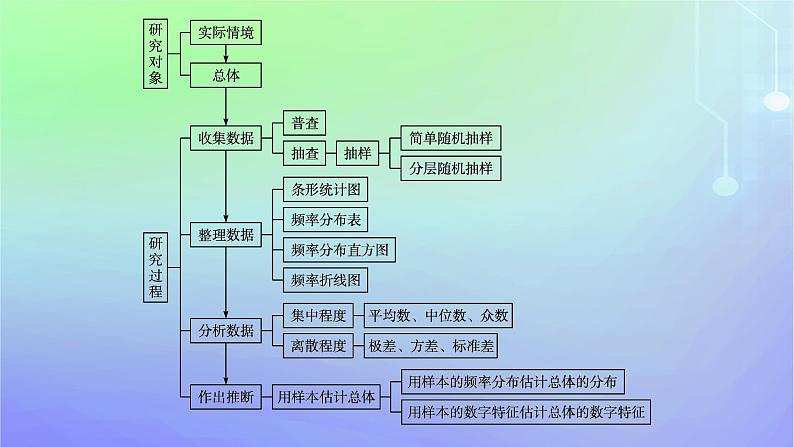
第六章本章总结提升网络构建·归纳整合专题突破·素养提升目录索引 网络构建·归纳整合专题突破·素养提升专题一 抽样的基本方法1.抽样方法有:简单随机抽样、分层随机抽样.一般地,当总体是由差异明显的几个层组成时选用分层随机抽样,否则考虑用简单随机抽样.选用简单随机抽样时,当总体容量较小时,采用抽签法;当总体容量较大、样本容量较小时,采用随机数法.2.抽样方法的选择与分层随机抽样中的计算是常考查的知识点,提升数学抽象和数学运算的核心素养.【例1】 (1)某中学组织“党史知识竞赛”活动,已知该校共有高中学生2 700人,用分层抽样的方法从该校高中学生中抽取一个容量为45的样本参加活动,其中高一年级抽取了16人,则该校高一年级学生人数为( )A.1 680 B.1 020 C.960 D.720C解析 设高一学生有x人,则 ,解得x=960,所以该校高一年级学生人数为960.(2)假设要考察某公司生产的袋装牛奶的三聚氰胺是否超标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,则得到的第4个样本个体的编号是 .(下面摘取了随机数表第7行至第9行) 068解析 由随机数表可以看出前4个样本的个体的编号是331,572,455,068.于是第4个样本个体的编号是068.规律方法 应用各种抽样方法抽样时要注意以下问题:(1)利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;(2)利用随机数法时注意编号位数要一致;(3)在分层随机抽样中,若在某一层抽到的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.变式训练1(1)下列抽样方法是简单随机抽样的是( )A.从平面直角坐标系中抽取5个点作为样本B.某饮料公司从仓库中的1 000箱饮料中一次性抽取20箱进行质量检查C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D.从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)D 解析 选项A中,平面直角坐标系中有无数个点,这与要求总体中的个体数有限不相符,故错误;B中,一次性抽取不符合简单随机抽样逐个抽取的特点,故错误;C中,50名战士是最优秀的,不符合简单随机抽样的等可能性,故错误.(2)某校为了了解学生学习的情况,采用分层随机抽样的方法从高一1 000人,高二1 200人,高三n人中抽取81人进行问卷调查,已知高二被抽取的人数为30,那么n=( )A.860 B.720 C.1 020 D.1 040D 专题二 用样本的频率分布估计总体分布1.频率分布直方图的构成及特征 2.掌握频率分布直方图的画法及其应用,重点提升数据分析与逻辑推理的核心素养.【例2】 从某中学参加2023年全国高中数学联赛预赛的500名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.(1)根据表中已知数据,分别计算①,②,③处的数值;(2)补全在区间[70,140]上的频率分布直方图;(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?解 (1)由表中数据知,随机抽取了50人,所以①为 =0.32,②为50×0.04=2,③为1-0.08-0.1-0.32-0.08-0.04-0.02=0.36.(2)经计算,频率分布表为根据频率分布表可补全频率分布直方图: (3)在随机抽取的50名同学中有4+2+1=7(名)同学成绩不低于110分,可以去参加决赛,故估计参加预赛的同学中能参加决赛的人数大概为规律方法 与频率分布直方图有关问题的常见类型及解题策略(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1可求出其他数据.(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.变式训练2对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生分别参加社区服务的次数,根据此数据作出了频率分布表和频率分布直方图,如图所示:(1)求表中M,p及图中a的值;(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数.(2)因为该校高三学生有240人,分组[10,15)的频率是0.25,所以估计该校高三学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.专题三 用样本估计总体的数字特征1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.2.掌握各个数字特征的意义及应用,重点提升数据分析与数学运算的核心素养.【例3】 某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,数据如下(单位:分):(1)请你分别计算这两组数据的平均数、中位数.(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人更合适?请说明理由.①从平均数看,甲、乙均为85分,平均水平相同;②从中位数看,乙的中位数大于甲,乙的成绩好于甲;③从方差来看,因为 ,所以甲的成绩较稳定;④从数据特点看,获得85分以上(含85分)的次数,甲有3次,而乙有4次,故乙的成绩好些;⑤从数据的变化趋势看,乙后几次的成绩均高于甲,且呈上升趋势,因此乙更具潜力.综上分析可知,甲的成绩虽然比乙稳定,但从中位数、获得好成绩的次数及发展势头等方面分析,乙具有明显优势,所以应派乙参赛更有望取得好成绩.规律方法 用样本的数字特征估计总体的数字特征应注意的问题(1)中位数用来描述数据的中心位置,众数体现了数据的最大集中点,平均数反映样本数据的总体水平.(2)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.变式训练3某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其质量(单位:克)是否合格,分别记录抽查数据,获得质量数据如下.甲:107,111,111,113,114,122乙:108,109,110,112,115,124(1)写出甲的众数和乙的中位数;(2)根据样本数据,计算甲、乙两个车间产品质量的平均数与方差,并说明哪个车间的产品的质量相对稳定.解 (1)甲的众数是111,乙的中位数是111. 专题四 样本的百分位数1.一般地,当总体是连续变量时,总体的p(0
第六章本章总结提升网络构建·归纳整合专题突破·素养提升目录索引 网络构建·归纳整合专题突破·素养提升专题一 抽样的基本方法1.抽样方法有:简单随机抽样、分层随机抽样.一般地,当总体是由差异明显的几个层组成时选用分层随机抽样,否则考虑用简单随机抽样.选用简单随机抽样时,当总体容量较小时,采用抽签法;当总体容量较大、样本容量较小时,采用随机数法.2.抽样方法的选择与分层随机抽样中的计算是常考查的知识点,提升数学抽象和数学运算的核心素养.【例1】 (1)某中学组织“党史知识竞赛”活动,已知该校共有高中学生2 700人,用分层抽样的方法从该校高中学生中抽取一个容量为45的样本参加活动,其中高一年级抽取了16人,则该校高一年级学生人数为( )A.1 680 B.1 020 C.960 D.720C解析 设高一学生有x人,则 ,解得x=960,所以该校高一年级学生人数为960.(2)假设要考察某公司生产的袋装牛奶的三聚氰胺是否超标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第7行第8列的数开始向右读,则得到的第4个样本个体的编号是 .(下面摘取了随机数表第7行至第9行) 068解析 由随机数表可以看出前4个样本的个体的编号是331,572,455,068.于是第4个样本个体的编号是068.规律方法 应用各种抽样方法抽样时要注意以下问题:(1)利用抽签法时要注意把号签放在不透明的容器中且搅拌均匀;(2)利用随机数法时注意编号位数要一致;(3)在分层随机抽样中,若在某一层抽到的个体数不是整数,应在该层剔除部分个体,使抽取个体数为整数.变式训练1(1)下列抽样方法是简单随机抽样的是( )A.从平面直角坐标系中抽取5个点作为样本B.某饮料公司从仓库中的1 000箱饮料中一次性抽取20箱进行质量检查C.某连队从200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D.从10个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)D 解析 选项A中,平面直角坐标系中有无数个点,这与要求总体中的个体数有限不相符,故错误;B中,一次性抽取不符合简单随机抽样逐个抽取的特点,故错误;C中,50名战士是最优秀的,不符合简单随机抽样的等可能性,故错误.(2)某校为了了解学生学习的情况,采用分层随机抽样的方法从高一1 000人,高二1 200人,高三n人中抽取81人进行问卷调查,已知高二被抽取的人数为30,那么n=( )A.860 B.720 C.1 020 D.1 040D 专题二 用样本的频率分布估计总体分布1.频率分布直方图的构成及特征 2.掌握频率分布直方图的画法及其应用,重点提升数据分析与逻辑推理的核心素养.【例2】 从某中学参加2023年全国高中数学联赛预赛的500名同学中,随机抽取若干名同学,将他们的成绩制成频率分布表,下面给出了此表中部分数据.(1)根据表中已知数据,分别计算①,②,③处的数值;(2)补全在区间[70,140]上的频率分布直方图;(3)若成绩不低于110分的同学能参加决赛,那么可以估计该校大约有多少学生能参加决赛?解 (1)由表中数据知,随机抽取了50人,所以①为 =0.32,②为50×0.04=2,③为1-0.08-0.1-0.32-0.08-0.04-0.02=0.36.(2)经计算,频率分布表为根据频率分布表可补全频率分布直方图: (3)在随机抽取的50名同学中有4+2+1=7(名)同学成绩不低于110分,可以去参加决赛,故估计参加预赛的同学中能参加决赛的人数大概为规律方法 与频率分布直方图有关问题的常见类型及解题策略(1)已知频率分布直方图中的部分数据,求其他数据,可根据频率分布直方图中的数据求出样本与整体的关系,利用频率和等于1可求出其他数据.(2)已知频率分布直方图,求某种范围内的数据,可利用图形及某范围结合求解.变式训练2对某校高三年级学生参加社区服务的次数进行统计,随机抽取M名学生,得到这M名学生分别参加社区服务的次数,根据此数据作出了频率分布表和频率分布直方图,如图所示:(1)求表中M,p及图中a的值;(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数.(2)因为该校高三学生有240人,分组[10,15)的频率是0.25,所以估计该校高三学生参加社区服务的次数在区间[10,15)内的人数为240×0.25=60.专题三 用样本估计总体的数字特征1.为了从整体上更好地把握总体规律,我们还可以通过样本数据的众数、中位数、平均数估计总体的集中趋势,通过样本数据的方差或标准差估计总体的离散程度.2.掌握各个数字特征的意义及应用,重点提升数据分析与数学运算的核心素养.【例3】 某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,数据如下(单位:分):(1)请你分别计算这两组数据的平均数、中位数.(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人更合适?请说明理由.①从平均数看,甲、乙均为85分,平均水平相同;②从中位数看,乙的中位数大于甲,乙的成绩好于甲;③从方差来看,因为 ,所以甲的成绩较稳定;④从数据特点看,获得85分以上(含85分)的次数,甲有3次,而乙有4次,故乙的成绩好些;⑤从数据的变化趋势看,乙后几次的成绩均高于甲,且呈上升趋势,因此乙更具潜力.综上分析可知,甲的成绩虽然比乙稳定,但从中位数、获得好成绩的次数及发展势头等方面分析,乙具有明显优势,所以应派乙参赛更有望取得好成绩.规律方法 用样本的数字特征估计总体的数字特征应注意的问题(1)中位数用来描述数据的中心位置,众数体现了数据的最大集中点,平均数反映样本数据的总体水平.(2)标准差(方差)反映了数据的离散与集中、波动与稳定的程度.标准差(方差)较大,数据的离散程度较大;标准差(方差)较小,数据的离散程度较小.变式训练3某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品,称其质量(单位:克)是否合格,分别记录抽查数据,获得质量数据如下.甲:107,111,111,113,114,122乙:108,109,110,112,115,124(1)写出甲的众数和乙的中位数;(2)根据样本数据,计算甲、乙两个车间产品质量的平均数与方差,并说明哪个车间的产品的质量相对稳定.解 (1)甲的众数是111,乙的中位数是111. 专题四 样本的百分位数1.一般地,当总体是连续变量时,总体的p(0
相关资料
更多









