北师大版 (2019)选择性必修 第一册第二章 圆锥曲线3 抛物线3.2 抛物线的简单几何性质评课课件ppt

这是一份北师大版 (2019)选择性必修 第一册第二章 圆锥曲线3 抛物线3.2 抛物线的简单几何性质评课课件ppt，共29页。PPT课件主要包含了目录索引，本节要点归纳等内容，欢迎下载使用。
基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
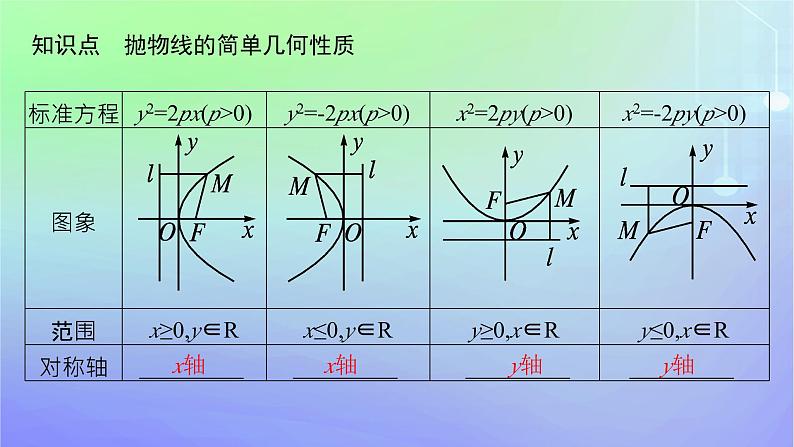
知识点　抛物线的简单几何性质
名师点睛1.抛物线没有渐近线,在画图时不要把抛物线画成双曲线一支的形状,因为双曲线的开口越来越开阔,而抛物线的开口越来越扁平.2.抛物线的顶点只有一个,抛物线的焦点总在对称轴上,抛物线的准线始终与对称轴垂直.
过关自诊1.[人教B版教材习题]已知抛物线y=4x2上的一点M的纵坐标为1,求点M到焦点的距离.
2.[人教B版教材习题]求抛物线y2=8x的焦点到直线x =0的距离.
探究点一　　已知抛物线的标准方程,研究抛物线的几何性质
【例1】 若抛物线y2=4x上一点P(x0,y0)到点(5,0)的距离最小,则点P的横坐标x0为(　　)A.1B.2C.3D.4
规律方法　把握三个要点确定抛物线的简单几何性质(1)开口:由抛物线标准方程看图象开口方向,关键是看准一次项是x还是y,一次项的系数是正还是负.(2)关系:顶点位于焦点与准线中间,准线垂直于对称轴.(3)定值:焦点到准线的距离为p;过焦点垂直于对称轴的弦(又称为通径)长为2p;离心率恒等于1.
变式训练1已知抛物线y2=8x,求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围.
解 抛物线y2=8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,[0,+∞).
探究点二　　抛物线的几何性质的应用
【例2】 (1)等腰直角三角形AOB内接于抛物线y2=2px(p>0),O为抛物线的顶点,OA⊥OB,则△AOB的面积是(　　)A.8p2B.4p2C.2p2D.p2
解析 因为抛物线的对称轴为x轴,内接△AOB为等腰直角三角形,AB是斜边,所以由抛物线的对称性知,直线AB与抛物线的对称轴垂直,从而直线OA与x轴的夹角为45°.
(2)已知抛物线的顶点在坐标原点,对称轴为x轴,且与圆x2+y2=4相交于A,B两点,|AB|=2 ,求抛物线方程.
解 由已知,抛物线的焦点可能在x轴正半轴上,也可能在负半轴上.故可设抛物线方程为y2=ax(a≠0).设抛物线与圆x2+y2=4的交点A(x1,y1),B(x2,y2).∵抛物线y2=ax(a≠0)与圆x2+y2=4都关于x轴对称,∴点A与点B也关于x轴∴所求抛物线方程是y2=3x或y2=-3x.
规律方法　利用抛物线的性质可以解决的问题
变式训练2求顶点在原点,对称轴是坐标轴,焦点在直线x-2y+2=0上的抛物线的标准方程. 
解 ∵焦点在直线x-2y+2=0上,且抛物线的顶点在原点,对称轴是坐标轴,∴焦点的坐标为A(0,1)或B(-2,0),若抛物线的焦点是A(0,1),则此抛物线方程为x2=4y.若抛物线的焦点是B(-2,0),则此抛物线方程为y2=-8x.故所求的抛物线的标准方程为x2=4y或y2=-8x.
探究点三　　抛物线的焦半径公式
【例3】 已知抛物线的顶点在原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,求m的值、抛物线的标准方程和准线方程.
规律方法　1.设抛物线的标准方程为x2=-2py(p>0),根据点M在抛物线上及条件|MF|=5,建立方程组求解.2.已知|MF|=5,可用焦半径公式求解.
变式训练3抛物线y2=2px(p>0)的焦点为F,O为坐标原点,M为抛物线上一点,且|MF|=3|OF|,△MFO的面积为16 ,则抛物线的方程为(　　)A.y2=6xB.y2=8xC.y2=16xD.y2=20x
1.知识清单:(1)抛物线的几何性质.(2)直线与抛物线的位置关系.2.方法归纳:待定系数法、数形结合法、代数法.3.常见误区:四种形式的抛物线性质混淆;忽略直线的特殊情况.
1.[2023甘肃兰州高三兰化一中校考]已知直线y=x-2与抛物线y2=2px(p>0)相交于A,B两点,满足OA⊥OB,则抛物线的方程为(　　)A.y2=2xB.y2=4xC.y2=6xD.y2=8x
3.抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值是(　　)
4.抛物线y2=4x的弦AB⊥x轴,若|AB|=4 ,则焦点F到直线AB的距离为　　　　　.