高中数学北师大版 (2019)选择性必修 第一册第六章 概率3 离散型随机变量的均值与方差3.1 离散型随机变量的均值评课课件ppt

这是一份高中数学北师大版 (2019)选择性必修 第一册第六章 概率3 离散型随机变量的均值与方差3.1 离散型随机变量的均值评课课件ppt，共36页。PPT课件主要包含了目录索引，求EX，提示X的分布列为，本节要点归纳等内容，欢迎下载使用。

基础落实·必备知识全过关
重难探究·能力素养全提升
成果验收·课堂达标检测
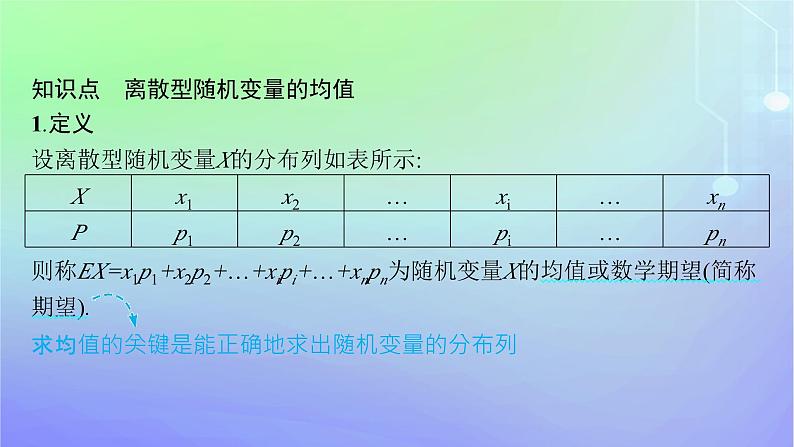
知识点　离散型随机变量的均值1.定义设离散型随机变量X的分布列如表所示:
则称EX=x1p1+x2p2+…+xipi+…+xnpn为随机变量X的均值或数学期望(简称期望).求均值的关键是能正确地求出随机变量的分布列
2.意义均值EX刻画的是X取值的“中心位置”,反映了离散型随机变量X取值的平均水平,是随机变量X的一个重要特征.名师点睛对离散型随机变量的均值的理解(1)均值是算术平均值概念的推广,是概率意义下的平均数.(2)离散型随机变量的均值EX是一个数值,是随机变量X本身固有的一个数字特征,它不具有随机性,反映的是随机变量取值的平均水平.(3)由离散型随机变量的均值的定义可知,它与离散型随机变量有相同的单位.
(4)若Y=aX+b(a,b是常数),X是随机变量,则Y也是随机变量,它们的分布列为
于是EY=(ax1+b)p1+(ax2+b)p2+…+(axn+b)pn+…=a(x1p1+x2p2+…+xnpn+…)+b(p1+p2+…+pn+…)=aEX+b,由此,我们得到了期望的一个性质:E(aX+b)=aEX+b.
过关自诊1.[人教A版教材习题]已知随机变量X的分布列为
提示 EX=1×0.1+2×0.3+3×0.4+4×0.1+5×0.1=2.8.
2.[人教A版教材习题]抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,求得分X的均值.
所求均值为EX=-1×0.5+1×0.5 =0.
3.[人教A版教材习题]甲、乙两台机床生产同一种零件,它们生产的产量相同,在1 h内生产出的次品数分别为X1,X2,其分布列分别为甲机床次品数的分布列
乙机床次品数的分布列
哪台机床更好?请解释你所得出结论的实际含义.
提示 甲机床的平均次品数EX1=0×0.4+1×0.3+2×0.2+3×0.1=1,乙机床的平均次品数EX2=0×0.3+1×0.5+2×0.2=0.9.由EX1=1,EX2=0.9可知,在1 h内,甲机床平均生产1个次品,乙机床平均生产0.9个次品,因此乙机床更好.
探究点一　　求离散型随机变量的均值
【例1】 [2021新高考Ⅰ,18]某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
规律方法　求离散型随机变量X的均值的步骤
变式训练1盒中装有5节同牌号的五号电池,其中混有2节废电池.现在不放回地每次取1节电池检验,直到取到好电池为止,求抽取次数X的分布列及均值.
探究点二　　离散型随机变量均值的性质
【例2】 已知随机变量X的分布列为
若Y=-2X,则EY=　　　　. 
变式探究本例条件不变,若ξ=aX+3,且Eξ=- ,求a的值.
规律方法　若给出的随机变量ξ与X的关系为ξ=aX+b,a,b为常数.一般思路是先求出EX,再利用公式E(aX+b)=aEX+b求Eξ.也可以利用X的分布列得到ξ的分布列,关键由X的取值计算ξ的取值,对应的概率相等,再由定义法求得Eξ.
变式训练2已知随机变量ξ和η,其中η=12ξ+7,且Eη=34,若ξ的分布列如下表,则m的值为(　　)
探究点三　　离散型随机变量均值的实际应用
【例3】 随机抽取某厂的某种产品200件,经质检,其中一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元,设1件产品的利润(单位:万元)为X.(1)求X的分布列;(2)求1件产品的平均利润(即X的均值);(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(2)EX=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34(万元).(3)设技术革新后的三等品率为x,则此时1件产品的平均利润为EX=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(0≤x≤0.29).依题意,EX≥4.73,即4.76-x≥4.73,解得x≤0.03,所以三等品率最多为3%.
规律方法　1.实际问题中的期望问题期望在实际生活中有着广泛的应用,如对体育比赛的成绩预测,消费预测,工程方案的预测,产品合格率的预测,投资收益的预测等方面,都可以通过随机变量的期望来进行估计.2.概率模型的三个解答步骤(1)审题,确定实际问题是哪一种概率模型,可能用到的事件类型,所用的公式有哪些.(2)确定随机变量的分布列,计算随机变量的期望.(3)对照实际意义,回答概率、均值等所表示的结论.
变式训练3节日期间,某种鲜花进货价是每束2.5元,销售价每束5元;节日卖不出去的鲜花以每束1.6元价格处理.根据前五年销售情况预测,节日期间这种鲜花的需求量X(单位:束)服从如下表所示的分布:
若进这种鲜花500束,则利润的均值为　　　　. 
解析 由分布列可以得到EX=200×0.2+300×0.35+400×0.3+500×0.15=340(束),则利润是(340×5+160×1.6)-500×2.5=706(元).
1.知识清单:(1)离散型随机变量的均值或数学期望(期望)的定义、性质.(2)离散型随机变量的均值或数学期望(期望)的实际应用.2.核心素养:数学运算、数学建模.3.常见误区:不能将问题情境正确地进行数学建模.
1.已知某离散型随机变量X服从的分布列如下,则随机变量X的数学期望EX等于(　　)
2.口袋中有编号分别为1,2,3的三个大小和形状相同的小球,从中任取2个,则取出的球的最大编号X的均值为(　　)
3.已知离散型随机变量X的分布列为
设Y=6X+1,则Y的数学期望EY=　 . 
4.某射手射击所得环数ξ的分布列如下:
已知ξ的均值Eξ=8.9,则y的值为　 . 
5.袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到1个黑球记0分,每取到1个白球记1分,每取到1个红球记2分,用X表示取得的分数.求:(1)X的分布列;(2)X的均值.