数学第一章 空间向量与立体几何1.4 空间向量的应用备课ppt课件

这是一份数学第一章 空间向量与立体几何1.4 空间向量的应用备课ppt课件，共26页。PPT课件主要包含了学习目标，情景导入，复习回顾，新知应用，牛刀小试，方法总结，课堂小结等内容，欢迎下载使用。
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.3.能用向量方法证明必修内容中有关直线、平面垂直关系的判定定理.4.能用向量方法证明空间中直线、平面的垂直关系.
1.空间中点、直线和平面的向量表示(1)点→点+位置向量 (2)线→点+方向向量 (3)平面→点+法向量
2.空间中直线、平面的平行
类似空间中直线、平面平行的向量表示，在直线与直线、直线与平面、平面与平面的垂直关系中，直线的方向向量、平面的法向量之间有什么关系？
02空间中直线、平面的垂直
空间中直线与直线的垂直
思考1：类似空间中直线、平面平行的向量表示，在直线与直线、直线与平面、平面与平面的垂直关系中，直线的方向向量、平面的法向量之间什么关系?
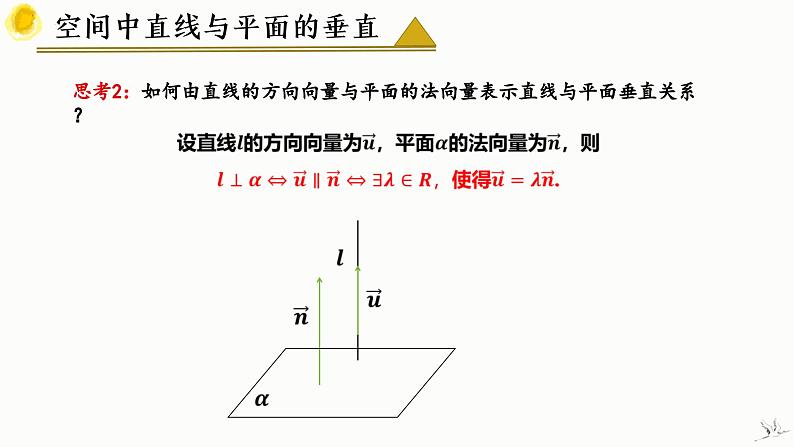
空间中直线与平面的垂直
思考2：如何由直线的方向向量与平面的法向量表示直线与平面垂直关系？
空间中平面与平面的垂直
思考3：由平面与平面的垂直关系，可以得到平面的法向量有什么关系？
1.判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.(1)若两条直线的方向向量的数量积为0,则这两条直线一定垂直相交.(　　)(2)若一直线与平面垂直,则该直线的方向向量与平面内的所有直线的方向向量的数量积为0.(　　)(3)两个平面垂直,则其中一平面内的直线的方向向量与另一平面内的直线的方向向量垂直.(　　)(4)若两平面α,β的法向量分别为u1=(1,0,1),u2=(0,2,0),则平面α,β互相垂直.(　　)
题型一：直线与直线垂直
利用向量方法证明线线垂直的方法(1)坐标法:建立空间直角坐标系,写出相关点的坐标,求出两直线方向向量的坐标,然后通过数量积的坐标运算法则证明数量积等于0,从而证明两条直线的方向向量互相垂直;(2)基向量法:利用空间向量的加法、减法、数乘运算及其运算律,结合图形,将两直线所在的向量用基向量表示,然后根据数量积的运算律证明两直线所在的向量的数量积等于0,从而证明两条直线的方向向量互相垂直.
2.在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC (2)BD1⊥EB1.
题型二：直线与平面垂直
3. 如图所示，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、D1B1的中点．求证：EF⊥平面B1AC.
证明：设正方体的棱长为2，以D为原点，以DA，DC，DD1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，则A(2,0,0)，C(0,2,0)，B1(2,2,2)，E(2,2,1)，F(1,1,2)．
利用空间向量证明线面垂直的方法(1)基向量法:选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,然后根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证得结论.(2)坐标法:建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,然后根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.(3)法向量法:建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,然后说明直线方向向量与平面法向量共线,从而证得结论.
题型三：平面与平面垂直
如图所示,在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=2,BB1=1,点E为BB1的中点,证明:平面AEC1⊥平面AA1C1C.
思路分析：要证明两个平面垂直,由两个平面垂直的条件,可证明这两个平面的法向量垂直,转化为求两个平面的法向量n1,n2,证明n1·n2=0.
解:由题意得AB,BC,B1B两两垂直.以点B为原点,BA,BC,BB1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系.则A(2,0,0),A1(2,0,1),
利用空间向量证明面面垂直通常有两个途径:1.利用两个平面垂直的判定定理将面面垂直问题转化为线面垂直进而转化为线线垂直;2.直接求解两个平面的法向量,由两个法向量垂直,得面面垂直.
利用空间向量证明面面垂直的方法