


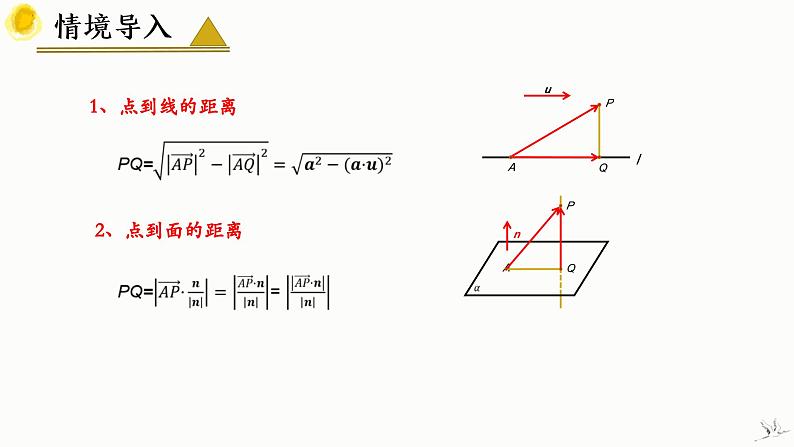


所属成套资源:高中数学人教A版(2019)选择性必修第一册同步精品课件
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用示范课课件ppt
展开这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用示范课课件ppt,共27页。PPT课件主要包含了学习目标,情景导入,情境导入,点到线的距离,点到面的距离,新知应用,课堂小结等内容,欢迎下载使用。
1.理解两异面直线所成角与它们的方向向量之间的关系,会用向量方法求两异面直线所成角.2.理解直线与平面所成角与直线方向向量和平面法向量夹角之间的关系,会用向量方法求直线与平面所成.3.理解二面角大小与两个面法向量夹角之间的关系,会用向量方法求二面角的大小。.
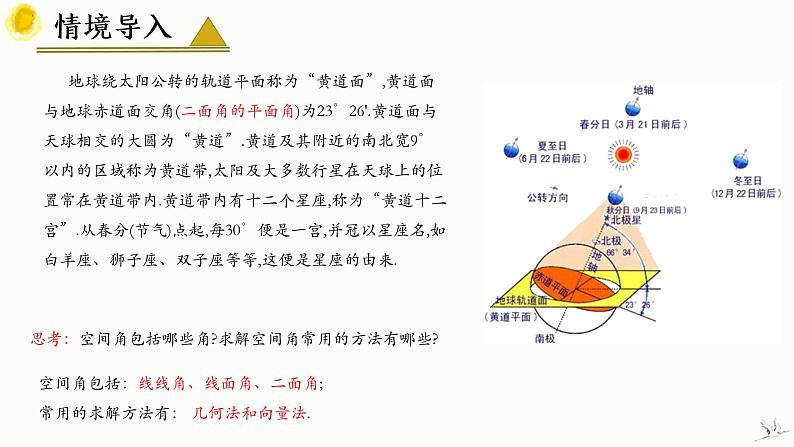
地球绕太阳公转的轨道平面称为“黄道面”,黄道面与地球赤道面交角(二面角的平面角)为23°26'.黄道面与天球相交的大圆为“黄道”.黄道及其附近的南北宽9°以内的区域称为黄道带,太阳及大多数行星在天球上的位置常在黄道带内.黄道带内有十二个星座,称为“黄道十二宫”.从春分(节气)点起,每30°便是一宫,并冠以星座名,如白羊座、狮子座、双子座等等,这便是星座的由来.
思考:空间角包括哪些角?求解空间角常用的方法有哪些?
空间角包括:线线角、线面角、二面角; 常用的求解方法有: 几何法和向量法.
02用空间向量研究夹角问题
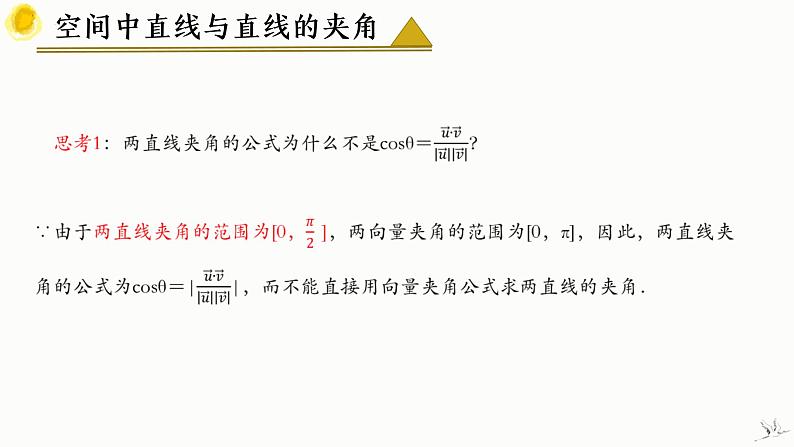
空间中直线与直线的夹角
根据前面数量积的学习,我们已经知道向量法求两条异面直线a,b的夹角的方法,思考:异面直线a,b的夹角为θ,方向向量分别为a,b,那么夹角θ与方向向量的夹角〈a,b〉之间有怎样的关系式?
相等或互补.两条直线的方向向量的夹角为锐角(直角)时相等,夹角为钝角时互补.
思考2:两条直线的方向向量的夹角与两异面直线所成角关系是什么?
空间中直线与平面的夹角
空间中平面与平面的夹角
平面与平面的夹角的定义:平面α与平面β相交,形成四个二面角,我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角.
题型一:异面直线所成角
1.已知四棱锥S-ABCD的底面是正方形且侧棱长与底面边长都相等,E是SB的中点,则AE,SD所成的角的余弦值为多少?
用坐标法求异面直线的夹角①建立恰当的空间直角坐标系;②找到两条异面直线的方向向量的坐标;③利用向量的夹角公式计算两直线的方向向量的夹角;④结合异面直线所成角的范围得到异面直线所成的角.
题型二:直线与平面所成角
求直线与平面的夹角的方法与步骤用向量法求直线与平面的夹角可利用向量夹角公式或法向量.利用法向量求直线与平面的夹角的基本步骤:
题型三:平面与平面所成角
利用向量法求两个平面夹角的步骤(1)建立空间直角坐标系;(2)分别求出二面角的两个半平面所在平面的法向量;(3)求两个法向量的夹角;(4)确定两平面夹角的大小.
相关课件
这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用课文课件ppt,共14页。PPT课件主要包含了礼物重力大小,礼物的重力,相反向量,所以PB⊥DE等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用授课ppt课件,共17页。PPT课件主要包含了θ∈0°90°,选择适当的基底表示,化为向量问题,进行向量运算,回到图形问题等内容,欢迎下载使用。
这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用备课课件ppt,共16页。PPT课件主要包含了空间中距离,两点间的距离,点到直线的距离,两平行线之间的距离,点到平面的距离,直线到平面的距离,两个平行平面间的距离,用垂直刻画,向量的模,空间两点间的距离等内容,欢迎下载使用。













