精品解析：广东省深圳市南山区太子湾学校2022-2023学年九年级上学期期中考试数学试题

这是一份精品解析：广东省深圳市南山区太子湾学校2022-2023学年九年级上学期期中考试数学试题，文件包含精品解析广东省深圳市南山区太子湾学校2022-2023学年九年级上学期期中考试数学试题原卷版docx、精品解析广东省深圳市南山区太子湾学校2022-2023学年九年级上学期期中考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。

2022−2023学年度第一学期期中教学质量监测
参考答案与试题解析
一、选择题（共10小题）
1. 已知四条线段a，b，c，d是成比例线段，其中，，，则线段a的长度为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据成比例线段的定义得到，然后利用比例的性质求a的值．
【详解】解：∵四条线段a、b、c、d是成比例线段，
∴，即，
∴．
故选：C．
【点睛】本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如（即），我们就说这四条线段是成比例线段，简称比例线段．
2. 用3个同样的小正方体摆出的几何体，从三个方向看到的图形分别如图，这个几何体是（　　）

A. B. C. D.
【答案】B
【解析】
【分析】根据三个方向看到的图形得出小正方体摆出的几何体即可．
【详解】解：根据题意得，小正方体摆出的几何体为：，
故选：B．
【点睛】本题考查实从不同方向看几何体．在画图时一定要将物体的边缘、棱、顶点都体现出来，看得见的轮廓线都画成实线，看不见的画成虚线，不能漏掉．
3. 已知关于的一元二次方程有两个不相等的实数根，则的取值范围是（ ）
A. ＜2 B. ＜3 C. ＜2 且≠0 D. ＜3且≠2
【答案】D
【解析】
【分析】根据方程有两个不相等的实数根结合二次项系数非0，即可得出关于k的一元一次不等式组，解不等式组即可得出结论．
【详解】∵关于x的一元二次方程(k−2)x2−2x+1=0有两个不相等的实数根，
∴ ，
解得：k<3且k≠2.
故选D.
【点睛】本题考查根的判别式，解题突破口是得出关于k的一元一次不等式组.
4. 下列说法中错误的是（ ）
A. 直角三角形斜边上的中线等于斜边的一半
B. 菱形的对角线平分一组对角，并且菱形是轴对称图形
C. 矩形的对角线把这个矩形分成4个等腰三角形
D. 对角线互相垂直的菱形是正方形
【答案】D
【解析】
【分析】根据直角三角形斜边上的中线性质对A进行判断；根据菱形的性质对B进行判断；根据矩形的性质对C进行判断，根据正方形的判定定理对D进行判断．
【详解】A、直角三角形斜边上的中线等于斜边的一半，该选项正确；
B、菱形的对角线平分一组对角，并且菱形是轴对称图形，该选项正确；
C、矩形的对角线把这个矩形分成4个等腰三角形，该选项正确；
D、对角线相等的菱形是正方形，该选项错误．
故选：D
【点睛】本题考查了菱形、矩形的性质以及正方形的判定定理，理解定理是关键．
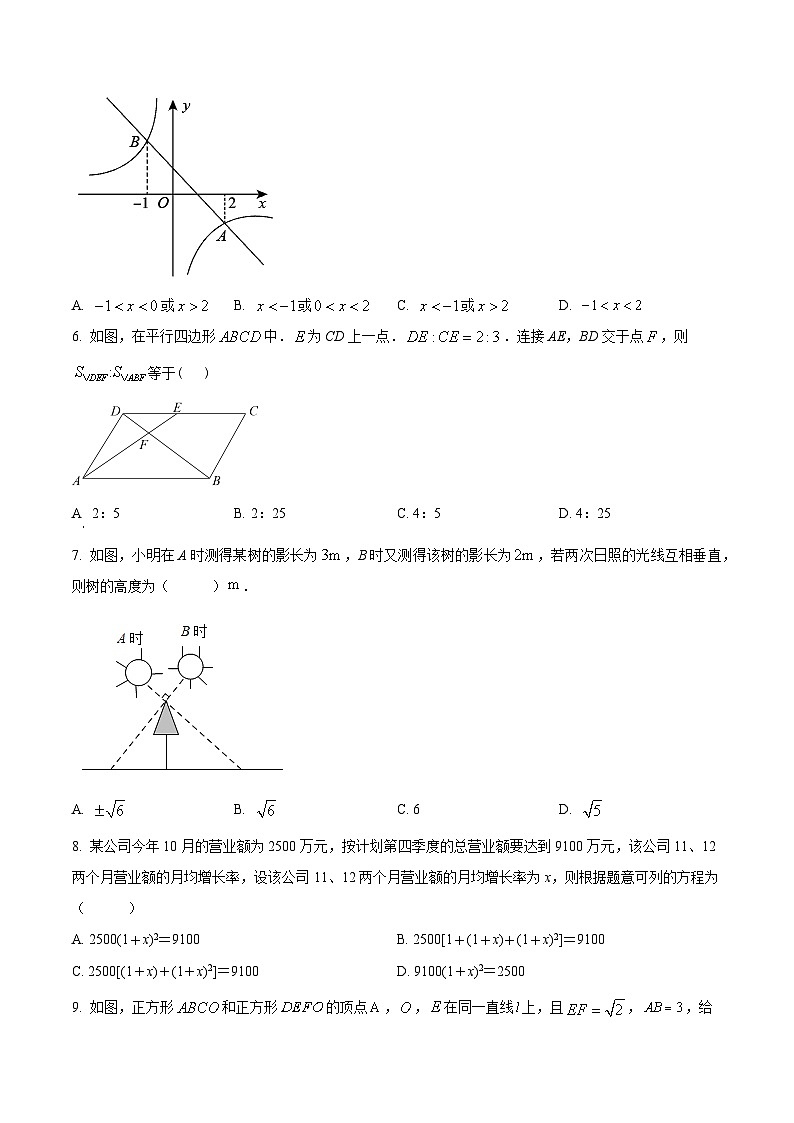
5. 如图，一次函数与反比例函数的图象相交于A，B两点，点A的横坐标为2，点B的横坐标为，则不等式的解集是（ ）

A. 或 B. 或 C. 或 D.
【答案】A
【解析】
【分析】根据不等式的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围进行求解即可．
【详解】解：由题意得不等式的解集即为一次函数图象在反比例函数图象下方时自变量的取值范围，
∴不等式的解集为或，
故选A．
【点睛】本题主要考查了一次函数与反比例函数综合，利用数形结合的思想求解是解题的关键．
6. 如图，在平行四边形中．为CD上一点．．连接AE，BD交于点，则等于( )

A. 2：5 B. 2：25 C. 4：5 D. 4：25
【答案】D
【解析】
【分析】由题意易得，然后可得，则有，进而根据相似三角形的面积比与相似比的关系可求解．
【详解】解：在平行四边形中，，
∴，
∵，
∴，
∴，
∴；
故选D．
【点睛】本题主要考查相似三角形的性质与判定及平行四边形的性质，熟练掌握相似三角形的性质与判定是解题的关键．
7. 如图，小明在A时测得某树的影长为，B时又测得该树的影长为，若两次日照的光线互相垂直，则树的高度为（　　　）．

A B. C. 6 D.
【答案】B
【解析】
【分析】根据题意，画出示意图，易得，进而可得，即，代入数据可得答案．
【详解】解：根据题意，作，树高为，且；

∵，
∴，
又，
∴，
∴，即，
解得（负值舍去）．
故选：B．
【点睛】本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
8. 某公司今年10月的营业额为2500万元，按计划第四季度的总营业额要达到9100万元，该公司11、12两个月营业额的月均增长率，设该公司11、12两个月营业额的月均增长率为x，则根据题意可列的方程为（　　　）
A. 2500(1＋x)2＝9100 B. 2500[1＋(1＋x)＋(1＋x)2]＝9100
C. 2500[(1＋x)＋(1＋x)2]＝9100 D. 9100(1＋x)2＝2500
【答案】B
【解析】
【分析】用增长后的量=增长前的量×（1+增长率）．即可表示出11月与12月的营业额，根据第四季的总营业额要达到9100万元，即可列方程．
【详解】解：设该公司11、12两个月营业额的月均增长率为x，
则可列方程为2500[1+（1+x）+（1+x）2]=9100，
故选：B．
【点睛】本题考查了由实际问题抽象出一元二次方程，平均增长率问题，若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2=b．
9. 如图，正方形和正方形的顶点，，在同一直线上，且，，给出下列结论：①；②；③；④的面积是．其中正确的结论为（ ）

A. ①③ B. ①④ C. ②③ D. ①③④
【答案】B
【解析】
【分析】①根据正方形的性质和平角的定义可求；
②根据正方形的性质可求，再根据线段的和差关系可求的长；
③首先证明，可得，之后证明即可；
④根据三角形面积公式即可求解．
【详解】解：①，，
，故①正确；
②，
，
，
，故②错误；
③四边形与四边形均为正方形，
，，
，
，
，
，
连接 交 于,过作交于，


四边形为矩形，
，，
，,
，
，
，，
，
，
在 与中，
，，
，
，故③错误；
④的面积，故④正确；
其中正确的结论为①④．
故选：B．
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，三角形面积，勾股定理，平角的定义，综合性较强，解决本题的关键是掌握正方形的性质．
10. 定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”．如图，在平面直角坐标系xOy中，矩形OABC的边OA＝3，OC＝4，点M(2，0)，在边AB存在点P，使得△CMP为“智慧三角形”，则点P的坐标为（　　）

A. (3，1)或(3，3) B. (3，)或(3，3)
C. (3，)或(3，1) D. (3，)或(3，1)或(3，3)
【答案】D
【解析】
【分析】由题意可知，“智慧三角形”是直角三角形，∠CPM＝90°或∠CMP＝90°，设P（3，a），则AP＝a，BP＝4−a；分两种情况：①若∠CPM＝90°，②若∠CMP＝90°，根据勾股定理分别求出CP2、MP2、CM2，并根据图形列出关于a的方程，解得a的值，则可得答案．
【详解】解：由题意可知，“智慧三角形”是直角三角形，∠CPM＝90°或∠CMP＝90°，
∴设P（3，a），则AP＝a，BP＝4−a；

①若∠CPM＝90°，在Rt△BCP中，由勾股定理得：
CP2＝BP2＋BC2＝（4−a）2＋9，
在Rt△MPA中，由勾股定理得：
MP2＝MA2＋AP2＝1＋a2，
在Rt△MPC中，由勾股定理得：
CM2＝MP2＋CP2＝1＋a2＋（4−a）2＋9＝2a2−8a＋26，
又∵CM2＝OM2＋OC2＝4＋16＝20，
∴2a2−8a＋26＝20，
∴（a−3）（a−1）＝0，
解得：a＝3或a＝1，
∴P（3，3）或（3，1）；
②若∠CMP＝90°，在Rt△BCP中，由勾股定理得：
CP2＝BP2＋BC2＝（4−a）2＋9，
在Rt△MPA中，由勾股定理得：
MP2＝MA2＋AP2＝1＋a2，
∵CM2＝OM2＋OC2＝20，
在Rt△MCP中，由勾股定理得：
CM2＋MP2＝CP2，
∴20＋1＋a2＝（4−a）2＋9，
解得：a＝．
∴P（3，）．
综上，P（3，）或（3，1）或（3，3）．
故选：D．
【点睛】本题考查了矩形的性质及勾股定理在几何图形坐标计算中的应用，数形结合、分类讨论并根据题意正确地列式是解题的关键．
二、填空题（共5小题）
11. 在菱形ABCD中，周长为20，对角线AC＝6，那么这个菱形的面积是_________.
【答案】24
【解析】
【分析】作出图形，根据菱形的四条边都相等求出菱形的边长，再根据菱形的对角线互相垂直平分求出，然后利用勾股定理列式求出，然后求出，再利用菱形的面积等于对角线乘积的一半列式计算即可得解．
【详解】解：如图，菱形的周长为20，

菱形的边长，，
对角线的长为6，
，
由勾股定理得，，
，
菱形的面积．
故答案为：24．
【点睛】本题考查了菱形的性质，主要利用了菱形的周长，菱形的对角线互相垂直平分的性质，熟记性质是解题的关键．
12. 已知，且，则值为__________．
【答案】12
【解析】
【分析】直接利用已知比例式假设出a，b，c的值，进而利用a+b-2c=6，得出答案．
【详解】解：∵，
∴设a=6x，b=5x，c=4x，
∵a+b-2c=6，
∴6x+5x-8x=6，
解得：x=2，
故a=12．
故答案为12．
【点睛】此题主要考查了比例的性质，正确表示出各数是解题关键．
13. 已知一元二次方程的两根分别为，则的值为_________．
【答案】
【解析】
【分析】一元二次方程的两根分别为，可得 再把要求值的代数式通分，再整体代入求值即可．
【详解】解：∵一元二次方程的两根分别为，
∴
∴
故答案为：-2
【点睛】本题考查是一元二次方程根与系数的关系，求解代数式的值，掌握“利用根与系数的关系构建整体代入求值”是解本题的关键．
14. 不透明布袋中装有除颜色外没有其他区别的1个红球和2个白球，从中一次性摸出两个球，两个球都是白球的概率是 _____．
【答案】
【解析】
【分析】根据题意可列出树状图进行求解即可．
【详解】解：由题意得：

∵有6种等可能的情况，从中一次性摸出两个球，两个球都是白球的有2种，
∴两次都摸出白球概率是．
故答案为：．
【点睛】本题主要考查了利用列表法或画树状图法求概率，熟练掌握利用树状图求解概率是解题的关键．
15. 如图，过原点的直线交双曲线于A、B两点，点C在x轴上，且，若的面积为6，则k的值为_____________．

【答案】3
【解析】
【分析】根据反比例函数的对称性和等腰三角形的性质得到S△ABC=2S△AOC=2=6，故可求解．
【详解】过点A作AE⊥OC，过点B作BD⊥OD，
∴S△AOE=
根据反比例函数的对称性可得AE=BD，
故S△ABC=S△AOC+S△OBC=×OC×AE+×OC×BD=2S△AOC
∵=AO
∴△AOC是等腰三角形，
∵AE⊥OC
∴E为CO中点
∴S△AOC=2S△AOE=2×，则S△ABC=2S△AOC=2=6
∴k=±3，
∵函数在一、三象限，故k=3
故答案为：3．

【点睛】此题主要考查反比例函数与几何综合，解题的关键是熟知反比例函数的图象与性质．
三、解答题（共9小题）
16. 按要求解下列方程：
（1）（配方法）；
（2）（公式法）．
【答案】（1），
（2），
【解析】
【分析】（1）先把1移到等号的右边，然后用配方法求解即可；
（2）先化为一般式，然后用公式法求解可．
【小问1详解】
解：，
，
，
，
，
或，
，；
【小问2详解】
解：，
，


，
，
，．
【点睛】本题考查了一元二次方程的解法，常用的方法有直接开平方法、配方法、因式分解法、求根公式法，熟练掌握各种方法是解答本题的关键．
17. （1）计算：；
（2）先化简、再求值：，其中．
【答案】（1）；（2）；．
【解析】
【分析】（1）根据零指数幂、乘方、二次根式的运算法则计算即可；
（2）根据分式的混合运算法则，化简后整体代入即可解决问题．
【详解】解：（1）原式

；
（2）原式


，
，
，
∴原式．
【点睛】本题考查零指数幂、乘方、二次根式、分式的混合运算法则等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
18. 为了解学生一周劳动情况，我市某校随机调查了部分学生的一周累计劳动时间，将他们一周累计劳动时间t（单位：时）划分为A：，B：，C：，D：四个组，并将调查结果绘制成如图所示的两幅不完整的统计图，根据图中所给信息解答下列问题：

（1）这次抽样调查共抽取_____________人，条形统计图中的_____________；
（2）在扇形统计图中，求B组所在扇形圆心角的度数，并将条形统计图补充完整；
（3）已知该校有1300名学生，根据调查结果，请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人？
（4）学校准备从一周累计劳动时间较长的两男两女四名学生中，随机抽取两名学生为全校学生介绍劳动体会，请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率．
【答案】（1）100；42
（2）72°；条形统计图见解析
（3）910； （4）
【解析】
【分析】（1）用D组的人数除以它所占的百分比得到调查的总人数，然后用调查的总人数乘以C组人数所占的百分比得到m的值；
（2）用360°乘以B组人数所占的百分比得到B组所在扇形圆心角的度数，再计算出B组人数，然后补全条形统计图；
（3）用1300乘以样本中C组和D组的人数所占百分比的和即可；
（4）画树状图展示所有12种等可能的结果，再找出一名男生和一名女生的结果数，然后根据概率公式计算．
【小问1详解】
解：这次抽样调查的总人数为（人），
所以；
故答案为：100；42；
【小问2详解】
解：B组所在扇形圆心角的度数为；
B组人数为（人），
条形统计图补充完整为：
【小问3详解】
解：（人），
所以估计该校一周累计劳动时间达到3小时及3小时以上的学生共有910人；
【小问4详解】
解：画树状图为：

共有12种等可能的结果，其中一名男生和一名女生的结果数为8，
所以恰好抽取到一名男生和一名女生的概率．
【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式计算事件A或事件B的概率．也考查了统计图．
19. 如图，在矩形ABCD中，E为AD边上的一点，过C点作CF⊥CE交AB的延长线于点F.

（1）求证：△CDE∽△CBF；
（2）若B为AF的中点，CB=3，DE=1，求CD的长.
【答案】（1）证明见解析；（2）CD=
【解析】
【分析】（1）如图，通过证明∠D=∠1，∠2=∠4即可得；
（2）由△CDE∽△CBF，可得CD：CB=DE：BF，根据B为AF中点，可得CD=BF，再根据CB=3，DE=1即可求得.
【详解】（1）∵四边形ABCD是矩形，

∴∠D=∠1=∠2+∠3=90° ，
∵CF⊥CE，
∴∠4+∠3=90°，
∴∠2=∠4，
∴△CDE∽△CBF；
（2）∵四边形ABCD是矩形，
∴CD=AB，
∵B为AF的中点，
∴BF=AB，
∴设CD=BF=x，
∵△CDE∽△CBF，
∴，
∴ ，
∵x>0，
∴x=，
即：CD=.
【点睛】本题考查了相似三角形的判定与性质：有两组角对应相等的两个三角形相似；两个三角形相似对应角相等，对应边的比相等．也考查了矩形的性质
20. “玫瑰香”葡萄品种是农科院研制的优质新品种，在被广泛种植，某葡萄种植基地2019年种植64亩，到2021年的种植面积达到100亩．
（1）求该基地这两年“玫瑰香”种植面积的平均增长率．
（2）某超市调查发现，当“玫瑰香”的售价为8元/千克时，每周能售出400千克，售价每上涨1元，每周销售量减少20千克，已知该超市“玫瑰香”的进价为6元/千克，为了维护消费者利益，物价部门规定，该水果售价不能超过15元．若使销售“玫瑰香”每周获利2240元，则售价应上涨多少元？
【答案】（1）该基地这两年“玫瑰香”种植面积的平均增长率为25%
（2）售价应上涨6元
【解析】
【分析】（1）设该基地这两年“玫瑰香”种植面积的平均增长率为x，根据该基地2019年及2021年“玫瑰香”的种植面积，即可得出关于x的一元二次方程，解之取其正值即可得出结论；
（2）设售价应上涨y元，则每天可售出（400-20y）千克，根据总利润＝每千克的利润×销售数量，即可得出关于y的一元二次方程，解之取其较大值即可得出结论．
【小问1详解】
解：（1）设该基地这两年“玫瑰香”种植面积的平均增长率为x，
依题意，得，
解得：，（不合题意，舍去）．
答：该基地这两年“玫瑰香”种植面积的平均增长率为25%．
【小问2详解】
解：设售价应上涨y元，则每天可售出（400-20y）千克，
依题意，得（8-6+y）（400-20y）＝2240，
整理，得，
解得，，
∵该水果售价不能超过15元，，，
∴不符合题意舍去，y＝6符合题意．
答：售价应上涨6元．
【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程，是解题的关键．
21. 如图，在中，，cm，，点从点出发沿方向以4cm/s的速度向点匀速运动，同时点从点出发沿方向以2cm/s的速度向点匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点运动的时间是ts．过点作于点，连接，．

（1）求证：四边形为平行四边形；
（2）①当______s时，四边形为菱形；
②当______s时，四边形为矩形．
【答案】（1）见解析 （2）①②
【解析】
【分析】（1）由题意得，再由含角的直角三角形的性质得DF=DC=，得到，然后证AEDF，即可得出结论；
（2）①由AE=AD，得四边形AEFD为菱形，得，进而求得的值；
②时，四边形DEBF为矩形，得到，再证AD=2AE，得，即可得出结论．
【小问1详解】
证明：由题意可知，
∵，
∴∠C=30°，
∴DF=DC=2t．
∵AE=2t，DF=2t，
∴AE=DF．
又∵DF⊥BC，AB⊥BC，
∴AEDF，
∴四边形AEFD为平行四边形．
【小问2详解】
解：①∵AB⊥BC，DF⊥BC，
∴AEDF．
∵AE=DF，AEDF，
∴四边形AEFD为平行四边形，
∴要使平行四边形AEFD为菱形，则需AE=AD，
即，
解得，
∴当时，四边形AEFD为菱形，
故答案为：10．
②要使四边形DEBF为矩形，则，
∴，
∴．
∵，
∴，
∴，
即，
解得．
即当
时，四边形DEBF为矩形，
故答案为：．
【点睛】本题考查了矩形的判定、平行四边形的判定与性质、菱形的判定、含30°角的直角三角形的性质等知识，熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．
22. 某数学活动小组在一次活动中，对一个数学问题做了如下研究：

【问题发现】（1）如图①，在等边三角形ABC中，点M是BC边上任意一点，连接AM，以AM为边作等边三角形AMN，连接CN，则∠ABC和∠ACN的数量关系为　 　；
【变式探究】（2）如图②，在等腰三角形ABC中，AB＝BC，点M是BC边上任意一点（不含端点B，C，连接AM，以AM为边作等腰三角形AMN，使∠AMN＝∠ABC，AM＝MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；
【解决问题】（3）如图③，在正方形ADBC中，点M为BC边上一点，以AM为边作正方形AMEF，点N为正方形AMEF的中心，连接CN，AB，AE，若正方形ADBC的边长为8，CN＝，直接写出正方形AMEF的边长．
【答案】（1） ；（2），理由见解析；（3）10
【解析】
【分析】（1）根据等边三角形的性质得到AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，证明△ABM≌△ACN，根据全等三角形的性质得到答案；
（2）证明△ABC∽△AMN．得到，再证明△ABM∽△ACN，根据相似三角形性质证明结论；
（3）证明△ABM～△ACN，根据相似三角形的性质求出BM，根据勾股定理计算即可．
【详解】解：（1）∵△ABC与△AMN是等边三角形，
∴AB＝AC，AM＝AN，∠BAC＝∠MAN＝60°，
∴∠BAM＝∠CAN，
在△ABM与△ACN中，
,
∴△ABM≌△ACN（SAS），
∴∠ABC＝∠ACN，
故答案为：∠ABC＝∠ACN；
（2）∠ABC＝∠ACN，
理由如下：∵AB＝BC，AM＝MN，
∴,
∴ ，又∠ABC＝∠AMN，
∴△ABC∽△AMN．
∴,
∵∠BAC＝∠MAN，
∴∠BAM＝∠CAN，
∴△ABM∽△ACN，
∴∠ABC＝∠ACN；
（3）∵四边形ADBC，AMEF为正方形，
∴∠ABC＝∠BAC＝45°，∠MAN＝45°，
∴∠BAC﹣∠MAC＝∠MAN﹣∠MAC，即∠BAM＝∠CAN，
∵,
∴,
又∠BAM＝∠CAN，
∴△ABM∽△ACN，
∴，即,
∴BM＝2，
∴CM＝6，
在Rt△AMC，AC＝8，CM＝6，
,
答：正方形AMEF的边长为10．
【点睛】本题是四边形综合题目，考查了正方形的性质、等边三角形的性质、等腰三角形的性质、全等三角形的性质和判定、相似三角形的性质和判定等知识；本题综合性强，有一定难度，证明三角形全等和三角形相似是解决问题的关键．