内蒙古自治区赤峰市松山区松山区第四中学2023-2024学年九年级上学期10月月考数学试题(无答案)

这是一份内蒙古自治区赤峰市松山区松山区第四中学2023-2024学年九年级上学期10月月考数学试题(无答案)，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
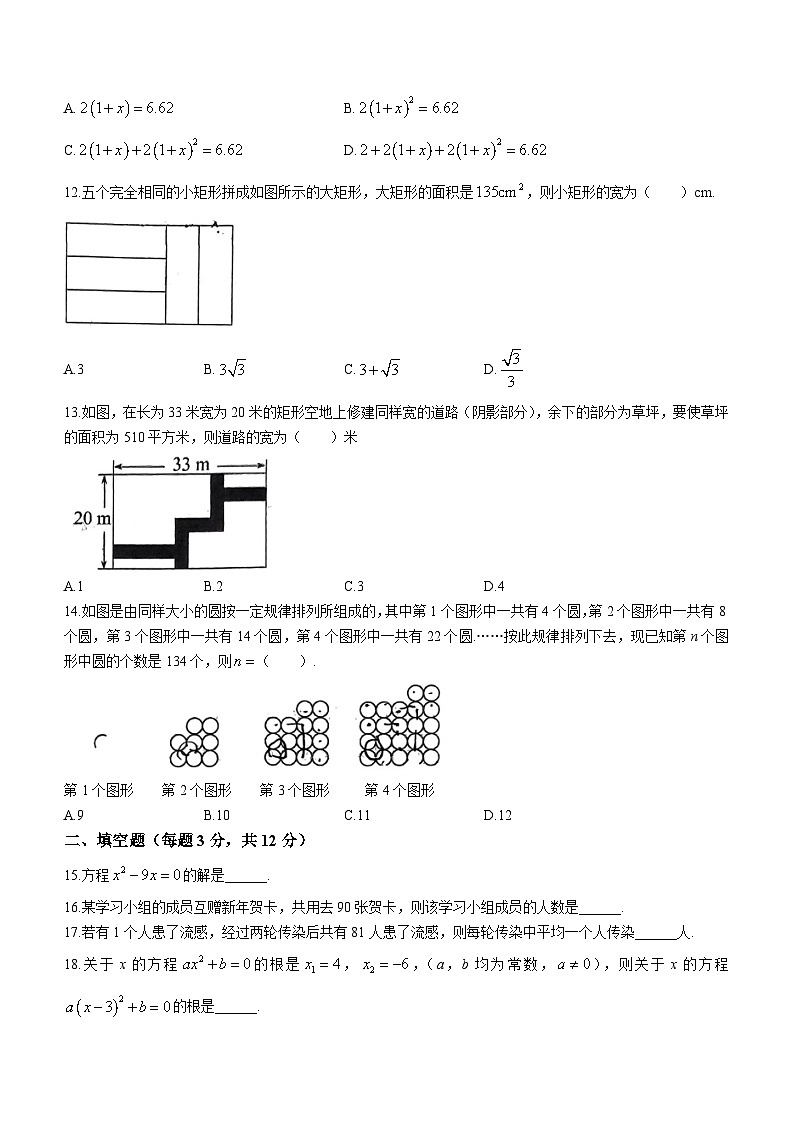
初三数学第一次月考试题班级：          姓名：一、选择题（每题3分，共42分）1.下列方程是一元二次方程的是（    ）A. B. C. D.2.如果关于x的一元二次方程，有一个解是0，那么m的值是（    ）A.3 B. C. D.0或3.将方程配方后，原方程变形为（    ）A. B. C. D.4.若是关于x的一元二次方程的解，则（    ）A. B. C.4 D.5.三角形的两边长分别为3和6，第三边的长是方程的一个根，则这个三角形的周长是（    ）A.9 B.12 C.13 D.12或136.若关于x的一元二次方程有两个实数根，则k的取值范围（    ）A. B. C.且 D.且7.某种植物的主干长出若干数目的支干，每个支干又长出相同数目的小分支，主干、支干和小分支的总数是21，则每个支干长出小分支的个数是（    ）A.6 B.4 C.3 D.58.已知关于x的一元二次方程的两个实数根为，，且，则k的值为（    ）A.5 B.6 C.7 D.89.已知m、n是一元二次方程的两个实数根，则代数式的值等于（    ）A.2019 B.2020 C.2021 D.202210.已知实数x，y满足，则的值是（    ）A.1或 B.或2 C.2 D.111.随着疫情影响消退和消费回暖，2023年电影市场向好，某电影上映的第一天票房约为2亿元，第二天、第三天单日票房持续增长，三天累计票房6.62亿元，若第二天、第三天单日票房按相同的增长率增长，设平均每天票房的增长率为x，则根据题意，下列方程正确的是（    ）A.  B.C. D.12.五个完全相同的小矩形拼成如图所示的大矩形，大矩形的面积是，则小矩形的宽为（    ）cm.A.3 B. C. D.13.如图，在长为33米宽为20米的矩形空地上修建同样宽的道路（阴影部分），余下的部分为草坪，要使草坪的面积为510平方米，则道路的宽为（    ）米A.1 B.2 C.3 D.414.如图是由同样大小的圆按一定规律排列所组成的，其中第1个图形中一共有4个圆，第2个图形中一共有8个圆，第3个图形中一共有14个圆，第4个图形中一共有22个圆.……按此规律排列下去，现已知第n个图形中圆的个数是134个，则（    ）.第1个图形    第2个图形    第3个图形     第4个图形A.9 B.10 C.11 D.12二、填空题（每题3分，共12分）15.方程的解是______.16.某学习小组的成员互赠新年贺卡，共用去90张贺卡，则该学习小组成员的人数是______.17.若有1个人患了流感，经过两轮传染后共有81人患了流感，则每轮传染中平均一个人传染______人.18.关于x的方程的根是，，（a，b均为常数，），则关于x的方程的根是______.三、解答题（共8题，满分96分）19.解方程（1）（配方法） （2）（公式法）（3） （4）20.如图，在矩形中，点E在边上，，.（1）尺规作图：在的延长线上求作点F，使.（要求：保留作图痕迹，不写作法）（2）在（1）的条件下，若等腰三角形的腰长恰好是关于x的一元二次方程的两个根，且，，过点E作于点，求线段的长.21.已知关于的x一元二次方程有两个不相等的实数根（1）求k的取值范围；（2）若此方程的两实数根，满足，求k的值.22.某种商品标价500元/件，经过两次降价后为405元/件，并且两次降价百分率相同.（1）求该种商品每次降价的百分率；（2）若该种商品进价为380元/件，两次降价共售出100件，若两次降价销售的总利润不低于3850元，则第一次降价后至少要售出该商品多少件？23.某商场销售一批儿童玩具，平均每天能售出20件，每件盈利40元，经调查发现；这种玩具的售价每降低1元，平均每天能多售出2件，设每件玩具降价x元。（1）降价后，每件玩具的利润为______元，平均每天的销售量为______件；（用含x的式子表示）（2）为了扩大销售，尽快减少库存，商场决定采取降价措施，但需要每天盈利1200元，那么每件玩具应降价多少元？24.为培养学生正确的劳动价值观和良好的劳动品质.某校为此规划出矩形苗圃.苗圃的一面靠墙（墙最大可用长度为15米）另三边用木栏围成，中间也用垂直于墙的木栏隔开分成面积相等的两个区域，并在如图所示的两处各留1米宽的门（门不用木栏），修建所用木栏总长28米，设矩形的一边长为x米.（1）矩形的面积为，求出的长（2）矩形的面积能否为，若能，请求出的长；若不能，请说明理由.25.配方法是数学中重要的一种思想方法。它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法。这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题，我们定义：一个整数能表示成（a、b是整数）的形式，则称这个数为“完美数”，例如，5是“完美数”，理由：因为，所以5是“完美数”.解决问题；（1）已知10是“完美数”，请将它写成（a、b是整数）的形式：______；（2）若可配方成（m、n为常数），则______.探究问题；（3）已知，则______.（4）已知（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由.26.如图，在四边形中，，，，，，动点P从点B出发，沿射线的方向以每秒2cm的速度向点C运动，动点Q从点A出发，在线段上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点P运动到点C时，点Q随之停止运动，设运动的时间t（秒）.（1）求、的代数表达式；（2）当t为何值时，四边形是平行四边形；（3）是否存在点P，使是等腰三角形？若存在，请求出所有满足要求的t的值；若不存在，请说明理由.