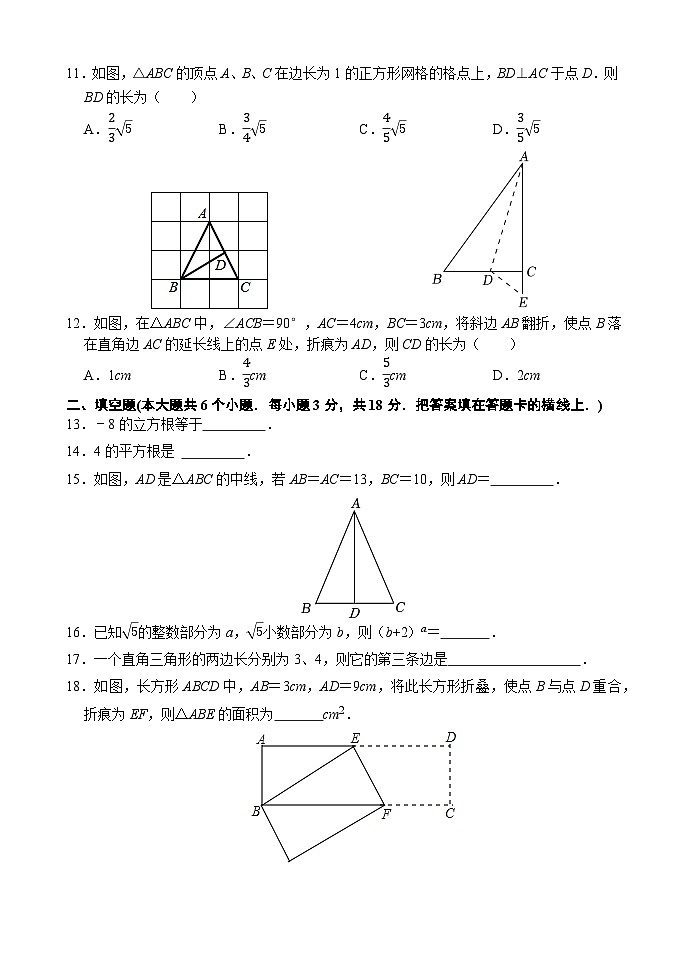
山东省济南兴济中学2023-2024学年八年级上学期数学10月份考试题

这是一份山东省济南兴济中学2023-2024学年八年级上学期数学10月份考试题，共4页。
2023～2024学年度第一学期阶段质量检测     八 年 级 数 学（2023.10）一、选择题（本大题共12个小题，每小题3分，共36分．）1．16的算术平方根是（　　）A．4 B．±4 C．±8 D．82．在2π，，，，3.14，3.868668666…（相邻两个8之间6的个数逐次加1）中，无理数的数是（　　）个A．2 B．3 C．4 D．53．下列运算正确的是（　　）A． B． C．2 D．34．下列各式中，是最简二次根式的是（　　）A． B． C． D．5．估计的值应在（　　）A．2和3之间 B．3和4之间 C．4和5之间 D．5和6之间6．下列运算正确的是（　　）A． B．－ C．±3 D．7．下列几组数据能作为直角三角形的三边长的是（　　）A．2，3，4 B．5，12，13 C．4，6，9 D．，，8．如图，有一个水池，水面是一边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺．如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面，这根芦苇的长度为（　　）尺．A．10 B．12 C．13 D．14                     9．正方体盒子的棱长为2，BC的中点为M，一只蚂蚁从A点爬到M点的最短距离为（　　）A． B． C．5 D．210．若△ABC中∠A、∠B、∠C的对边分别是a，b，c，下列条件不能说明△ABC是直角三角形的是（　　）A．b2＝（a+c）（a﹣c） B．a：b：c＝1：：2 C．∠C＝∠A﹣∠B D．∠A：∠B：∠C＝3：4：511．如图，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D．则BD的长为（　　）A． B． C． D．      12．如图，在△ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CD的长为（　　）A．1cm B．cm C．cm D．2cm二、填空题(本大题共6个小题．每小题3分，共18分．把答案填在答题卡的横线上．)13．﹣8的立方根等于　     　．14．4的平方根是 　     　．15．如图，AD是△ABC的中线，若AB＝AC＝13，BC＝10，则AD＝　     　．16．已知的整数部分为a，小数部分为b，则（b+2）a＝　   　．17．一个直角三角形的两边长分别为3、4，则它的第三条边是　               　．18．如图，长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为　   　cm2．  三、解答题(本大题共7个小题，共46分．解答应写出文字说明，证明过程或演算步骤．)19．(本小题满分6分) 计算：（1）；      （2）3．     （3）； 20．(本小题满分6分) 计算：（1）．            （2）．           （3）（2）2； 21．(本小题满分6分)解方程：（1）x2＝25；       （2）（x﹣1）2＝16；   、（3）（x﹣2）3＝﹣125． 22．(本小题满分6分)已知2a+1的一个平方根是3，1﹣b的立方根为﹣1．（1）求a与b的值；（2）求3a+2b的算术平方根．   23．(本小题满分7分)如图，在四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°．（1）求证：CD⊥AD；（2）求四边形ABCD的面积．  24．(本小题满分7分)在△ABC中，AB＝15，BC＝14，AC＝13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路：作AD⊥BC于D，设BD＝x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，建立方程模型求出x→利用勾股定理求出AD的长，再计算三角形的面积．请你按照他们的解题思路完成解答过程．    25．(本小题满分8分)如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝6cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒．（1）求BC边的长；（2）当△ABP为直角三角形时，求t的值；