江苏省扬州市江都区八校2023—2024学年八年级上学期10月检测数学试卷

这是一份江苏省扬州市江都区八校2023—2024学年八年级上学期10月检测数学试卷，文件包含八年级数学试卷参考答案docx、八年级试卷docx等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。
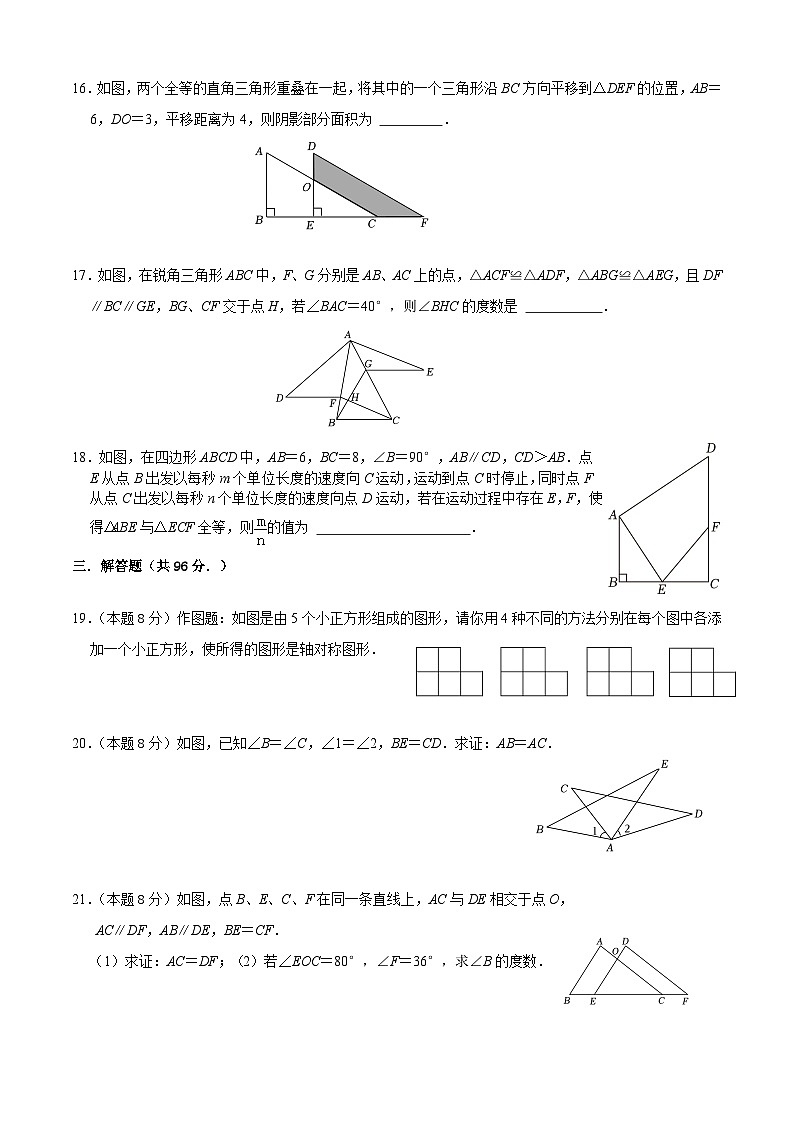
八年级数学试卷参考答案一．选择题（每题3分，共计24分. ）1．D．2．C．3.A．4．D．5．D．6．C．7．D．8．B．二．填空题（每空3分，共30分．）9．四个图形分别是正三角形、等腰梯形、长方形、正五边形，它们全部是轴对称图形，其中对称轴的条数最少的图形是　等腰梯形　．10．在平面镜里看到背后墙上，电子钟示数如图所示，这时的时间应是 　21：05　．11．如图，△ABC与△A'B'C'关于直线l对称，则∠B的度数为 　100°　．12．如图，已知△ABC≌△ADC，∠BAC＝60°，∠ACD＝23°，那么∠D＝　97　度．13．为了庆祝神舟十五号的成功发射，学校组织了一次小制作展示活动，小明计划制作一个如图所示的简易模型，已知该模型满足△ABD≌△ACE，点B和点C是对应顶点，若AB＝8cm，AD＝3cm，则DC＝　5　cm．14．淇淇用图1的六个全等△ABC纸片拼接图2所示的外轮廓是正六边形​，如果用若干个△ABC纸片按照图3所示的方法拼接成外轮廓是正n变形图案，那么n的值为 　9　．15．如图，是4×4正方形网格，其中已有4个小方格涂成了黑色．现在要从其余白色小方格中选出一个也涂成黑色，使整个黑色部分图形构成轴对称图形，这样的白色小方格有 　3　种选择．16．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿BC方向平移到△DEF的位置，AB＝6，DO＝3，平移距离为4，则阴影部分面积为 　18　．17．如图，在锐角三角形ABC中，F、G分别是AB、AC上的点，△ACF≌△ADF，△ABG≌△AEG，且DF∥BC∥GE，BG、CF交于点H，若∠BAC＝40°，则∠BHC的度数是 　100°　。18．如图，在四边形ABCD中，AB＝6，BC＝8，∠B＝90°，AB∥CD，CD＞AB．点E从点B出发以每秒m个单位长度的速度向C运动，运动到点C时停止，同时点F从点C出发以每秒n个单位长度的速度向点D运动，若在运动过程中存在E，F，使得△ABE与△ECF全等，则的值为 　1或　．三．解答题（共96分．）19．（本题8分）解：如图所示：答案不唯一，．.........................................................................................每种方法2分，共计8分20．（本题8分）证明：∵∠1＝∠2，∴∠BAE＝∠CAD，..............................................1分在△BAE与△CAD中，，∴△BAE≌△CAD（AAS），..............................................7分∴AB＝AC．..............................................8分21．（本题8分）（1）证明：∵AC∥DF，AB∥DE，∴∠F＝∠ACB，∠B＝∠DEF，..............................................1分∵BE＝CF，∴BE+EC＝CF+EC，∴BC＝EF，..............................................2分在△ABC与△DEF中，，∴△ABC≌△DEF（ASA），∴AC＝DF；..............................................4分（2）解：∵AC∥DF，∴∠F＝∠ACB，∵∠F＝36°，∴∠ACB＝36°．∵∠EOC＝80°，∴∠DEF＝180°﹣36°﹣80°＝64°，∵AB∥DE，∴∠B＝∠DEF＝64°．..............................................8分22．（本题8分）证明：在△ACB和△ADB中，，∴△ACB≌△ADB（SSS），..............................................3分∴∠CAE＝∠DAE，..............................................4分在△ACE和△ADE中，，∴△ACE≌△ADE（SAS），∴CE＝DE．..............................................8分23．（本题10分）（1）证明：∵AB∥DE，∴∠ABC＝∠DEF，...........................................1分在△ABC与△DEF中，∴△ABC≌DEF（ASA）；............................................5分（2）解：∵△ABC≌△DEF，∴BC＝EF∴BF+FC＝EC+FC，∴BF＝EC，∵BE＝100m，BF＝30m，∴FC＝100﹣30﹣30＝40m．............................................10分答：FC的长是40m．24．（本题10分）（1）解：小虎同学的证明过程中，第二步出现错误，故答案为：二；............................................3分（2）证明：∵∠ADC＝∠AEB＝90°，∴∠BDC＝∠CEB＝90°，............................................4分在△DOB和△EOC中，，∴△DOB≌△EOC（AAS），∴OD＝OE，............................................7分在Rt△ADO和Rt△AEO中，，∴Rt△ADO≌Rt△AEO（HL），∴∠1＝∠2．............................................10分25．（本题10分）解：（1）..........................................3分（2）①..........................................7分（作图方法不唯一）②.........................................10分（作图用的什么方法就选择什么依据）26．（本题10分）解：（1）答案为：或；.........................................4分（2）△APQ≌△DEF，即，对应顶点为A与D，P与E，Q与F；①当点P在AC上，如图②﹣1所示：此时，AP＝4，AQ＝5，∴点Q移动的速度为5÷（4÷3）＝cm/s，.........................................7分②当点P在AB上，如图②﹣2所示：此时，AP＝4，AQ＝5，即，点P移动的距离为9+12+15﹣4＝32cm，点Q移动的距离为9+12+15﹣5＝31cm，∴点Q移动的速度为31÷（32÷3）＝cm/s，.........................................10分综上所述，两点运动过程中的某一时刻，恰好△APQ≌△DEF，点Q的运动速度为cm/s或cm/s．27．（本题12分）（1）解：∵在△ADC和△EDB中，∴△ADC≌△EDB（SAS），故选B；.........................................3分（2）解：∵由（1）知：△ADC≌△EDB，∴BE＝AC＝6，AE＝2AD，∵在△ABE中，AB＝8，由三角形三边关系定理得：8﹣6＜2AD＜8+6，∴1＜AD＜7，故选C．.........................................6分（3）证明：延长AD到M，使AD＝DM，连接BM，∵AD是△ABC中线，∴CD＝BD，∵在△ADC和△MDB中∴△ADC≌△MDB，∴BM＝AC，∠CAD＝∠M，∵AE＝EF，∴∠CAD＝∠AFE，∵∠AFE＝∠BFD，∴∠BFD＝∠CAD＝∠M，∴BF＝BM＝AC，即AC＝BF．.........................................12分28．（本题12分）解：（1）如图1，延长EB到G，使BG＝DF，连接AG．∵在△ABG与△ADF中，，∴△ABG≌△ADF（SAS）．∴AG＝AF，∠1＝∠2，∴∠1+∠3＝∠2+∠3＝∠BAD＝∠EAF．∴∠GAE＝∠EAF．又AE＝AE，易证△AEG≌△AEF．∴EG＝EF．∵EG＝BE+BG．∴EF＝BE+FD.........................................3分（2）（1）中的结论EF＝BE+FD仍然成立．理由是：如图2，延长EB到G，使BG＝DF，连接AG．∵∠ABC+∠D＝180°，∠ABG+∠ABC＝180°，∴∠ABG＝∠D，∵在△ABG与△ADF中，，∴△ABG≌△ADF（SAS）．∴AG＝AF，∠1＝∠2，∴∠1+∠3＝∠2+∠3＝∠BAD＝∠EAF．∴∠GAE＝∠EAF．又AE＝AE，∴△AEG≌△AEF．∴EG＝EF．∵EG＝BE+BG．∴EF＝BE+FD.........................................9分（3）EF＝BE+FD或EF＝BE﹣FD或EF＝FD﹣BE．.........................................12分