

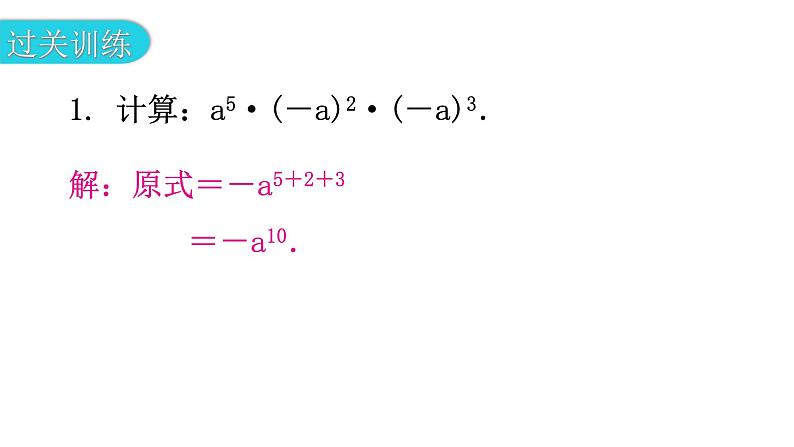

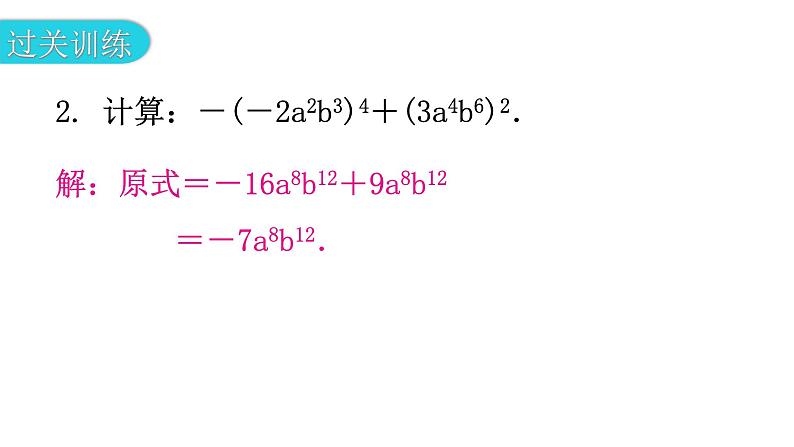
所属成套资源:全套北师大版七年级数学下册专题教学课件
北师大版七年级数学下册专题一第一章整式的乘除易错点例析教学课件
展开
这是一份北师大版七年级数学下册专题一第一章整式的乘除易错点例析教学课件,共11页。
专题一 本章易错点例析【例1】计算:(-x)3·(-x)5.错解:原式=(-x)3×5=(-x)15=-x15.错解分析:该题应根据“同底数幂相乘,底数不变,指数相加”的性质进行计算,而错解犯了变指数相加为指数相乘的错误,与幂的乘方混淆,把(-x)3·(-x)5误解成[(-x)3]5.正解:原式=(-x)3+5=(-x)8=x8.1. 计算:a5·(-a)2·(-a)3.解:原式=-a5+2+3=-a10.【例2】计算:(x6)2(-x3)2.错解:原式=x36(-x9)=-x45.错解分析:本题错在把指数进行乘方运算了,把(x6)2误解为x36,把(-x3)2误解为-x9,正确的解法应按幂的运算性质“底数不变,指数相乘”进行计算.正解:原式=x12·x6=x18.2. 计算:-(-2a2b3)4+(3a4b6)2.解:原式=-16a8b12+9a8b12=-7a8b12.【例3】计算:(-3×103)3.错解:原式=(-3)×(103)3=-3×109.错解分析:积的乘方的运算性质是“先把每个因式分别乘方,再把所得的幂相乘”,错解中没有把-3这个因数乘方.正解:原式=(-3)3×(103)3=-27×109.3. 计算:-(-4×104)2.解:原式=-(-4)2×(104)2=-16×108.【例4】 计算:(-a)3(-2a)2.错解:原式=[(-a)(-2a)]6=(2a2)6=64a12.错解分析:错在将底数乘以底数,指数乘以指数了,实际上,应先进行幂的运算,然后再根据单项式的乘法法则进行计算.正解:原式=(-a3)(4a2)=-4a5.4. 计算:(-2a2b3)4+(-a)8·(2b4)3.解:原式=16a8b12+a8·8b12=(16+8)a8b12=24a8b12.【例5】 计算:3x(2x2-y+1).错解:原式=6x3-3xy.错解分析:错在3x与1没有相乘,即漏乘了最后的常数项.正解:原式=6x3-3xy+3x.5. 计算: 4xy·(-3x2+2xy-1).解:原式=4xy·(-3x2)+4xy·2xy+4xy·(-1)=-12x3y+8x2y2-4xy.






