北师大版七年级数学下册专题一第二章相交线与平行线易错点例析教学课件

这是一份北师大版七年级数学下册专题一第二章相交线与平行线易错点例析教学课件，共23页。
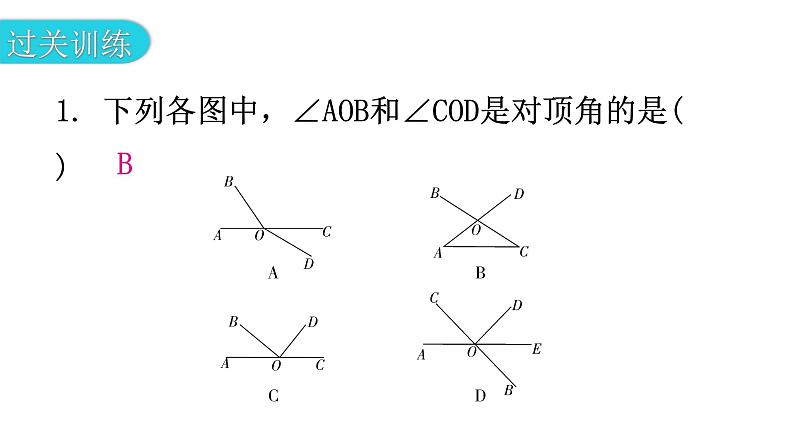
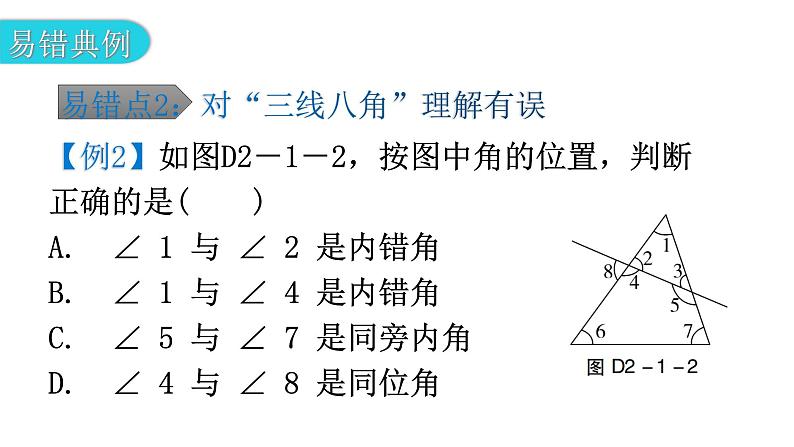
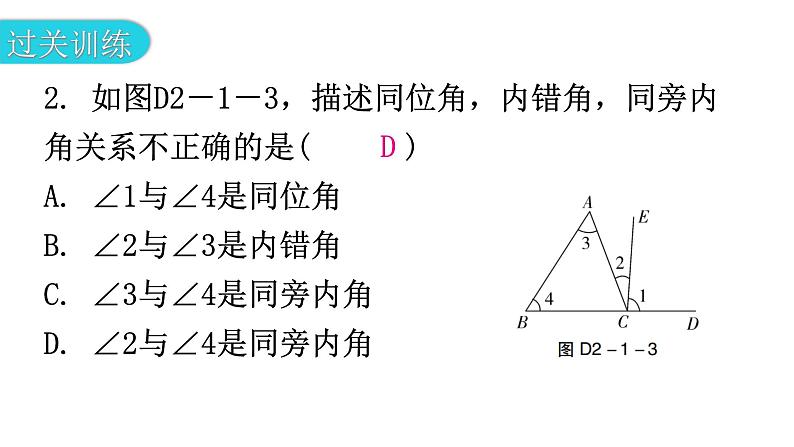
专题一 本章易错点例析【例1】如图D2－1－1，三条直线交于一点，任意找出图中的四对对顶角．错解:对顶角有：(1)∠AOC与∠BOD；(2)∠AOF与∠BOD；(3)∠COF与∠DOE；(4)∠AOC与∠BOE．错解分析:错解中把有公共顶点的角误认为是对顶角，导致(2)和(4)错误．如果对对顶角的概念没有真正理解和掌握，在比较复杂的图形识别中会产生错误．对顶角就是一个角的两边分别是另一个角的两边的反向延长线．正解:对顶角有：(1)∠AOC与∠BOD；(2)∠BOE与∠AOF；(3)∠COF与∠DOE；(4)∠COE 与∠DOF．(答案不唯一：∠AOE 与∠BOF，∠BOC与∠AOD也是对顶角)1. 下列各图中，∠AOB和∠COD是对顶角的是( )B【例2】如图D2－1－2，按图中角的位置，判断正确的是( )A. ∠ 1 与 ∠ 2 是内错角B. ∠ 1 与 ∠ 4 是内错角C. ∠ 5 与 ∠ 7 是同旁内角D. ∠ 4 与 ∠ 8 是同位角错解:选A，B，D. 错解分析:本题考查的是当两条直线被第三条直线所截时，如何准确地找到同位角、内错角 、同旁内角．要想准确地解决这类问题，首先要明确三种角的位置特点：在被截直线的内部，截线两旁的角叫做内错角；在被截直线的内部，截线同旁的角叫做同旁内角；在被截直线的上方(或下方)，截线同旁的角叫做同位角．其次要搞清楚被哪条直线所截.正解:选C．2. 如图D2－1－3，描述同位角，内错角，同旁内角关系不正确的是( )A. ∠1与∠4是同位角B. ∠2与∠3是内错角C. ∠3与∠4是同旁内角D. ∠2与∠4是同旁内角D【例3】 如图D2－1－4，已知直线AB，CD被直线EF，GH所截，∠1＋∠2＝180°，则________∥________．错解:EF，GH.因为∠1＋∠2＝180°，根据同旁内角互补，两直线平行，可知EF∥GH．错解分析:虽然“同旁内角互补，两直线平行”，但∠1与∠2是对直线AB，CD而言的，不能判定EF，GH的关系．正解:AB，CD. 3. 如图D2－1－5，直线AB，CD被直线EF，GH所截，且∠1＝∠2，求证：∠3＋∠4＝180°．证明：因为∠1＝∠2,∠2＝∠5，所以∠1＝∠5.所以AB∥CD.所以∠3＋∠4＝180°【例4】如图D2－1－6，在直角三角形ABC中，∠ACB＝90°，直线DE过点C，且DE∥AB，若∠ACD＝50°，则∠A＝________，∠B＝________. 错解：由两条平行线AB，CD被第三条直线AC或者BC所截，内错角相等，得∠B＝∠ACD＝50°，∠A＝∠BCE＝90°－∠ACD＝40°.错解分析：对几何图形观察认识不清楚而出错，观察三条直线中，AB，CD被第三条直线AC所截时，∠A与∠ACD是内错角，AB，CD被第三条直线BC所截时，∠B与∠BCE是内错角，∠B与∠ACD不是内错角.正解：由两直线平行，内错角相等,得∠A＝∠ACD＝50°，∠B＝90°－∠A＝40°.【例5】 如图D2－1－8，直线AB，CD分别和直线MN相交于点E，F，EG平分∠BEN，FH平分∠DFN．若AB∥CD，你能说明EG 和FH也平行吗?  错解分析：在复杂的图形中正确地找出同位角、内错角或同旁内角，是运用平行线的判定或性质的前提．认清一对同位角、内错角或同旁内角的关键是弄清截线和被截线，截线就是它们的公共边，其余两条边就是被截线．而∠BEG 和∠DFH不是直线EG，FH被某条直线所截得的同位角， 所以由∠BEG＝∠DFH不能判定EG∥FH． 4. 如图D2－1－7，直线AD和BC相交于O，AB∥CD，AD⊥BC于点O，∠B＝50°，求∠A和∠C．解：因为AD⊥BC，所以∠AOB＝90°.因为∠B＝50°，所以∠A＝90°－50°＝40°.因为AB∥CD，所以∠C＝∠B＝50°．5. 如图D2－1－9，已知∠1＋∠2＝180°，∠3＝∠B. 试判断直线DE和直线BC的位置关系,并说明理由．解:DE∥BC.理由如下：因为∠1＋∠2＝180°，∠1＝∠4，所以∠2＋∠4＝180°.所以AB∥EH.所以∠3＋∠BDE＝180°.因为∠B＝∠3，所以∠B＋∠BDE＝180°.所以DE∥BC. 6.如图D2－1－10，已知点D，E分别在三角形ABC的边AB，AC上，DE∥BC．（1）若∠ABC＝80°，∠AED＝40°，求∠A的度数；（2）若∠BFD＋∠CEF＝180°，求证：∠EDF＝∠C．（1）解：因为DE∥BC，所以∠C＝∠AED＝40°．因为∠A＋∠ABC＋∠C＝180°，所以∠A＝180°－∠ABC－∠C＝180°－80°－40°＝60°．（2）证明：因为∠BFD＋∠DFE＝180°，∠BFD＋∠CEF＝180°，所以∠DFE＝∠CEF．所以DF∥AC．所以∠EDF＝∠AED．因为DE∥BC，所以∠AED＝∠C．所以∠EDF＝∠C．