
苏科版初中数学九年级上册第三章《数据的集中趋势和离散程度》单元测试卷(较易)(含答案解析)
展开苏科版初中数学九年级上册第三章《数据的集中趋势和离散程度》单元测试卷
考试范围:第三章 考试时间 :120分钟 总分 :120分
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1.某手表厂抽查了只手表的日走时误差,数据如下表所示单位::
日走时误差 | ||||
只数 |
则这只手表的平均日走时误差单位:是( )
A. B. C. D.
2.已知个数、、、、的平均数是,则数据、、、、的平均数为
( )
A. B. C. D.
3.在竞选班干部时,某同学表达能力、组织能力、责任心的得分分别是分,分,分.若依次按,,的比例确定最终得分,则这个人的最终得分是( )
A. 分 B. 分 C. 分 D. 分
4.若一组数据,,,,的众数为,则这组数据的中位数为( )
A. B. C. D.
5.已知一组数据:,,,,,这组数据的平均数和中位数分别是( )
A. , B. , C. , D. ,
6.某校举行“汉字听写比赛”,个班级代表队的正确答题数如图.这个正确答题数所组成的一组数据的中位数和众数分别是( )
A. , B. , C. , D. ,
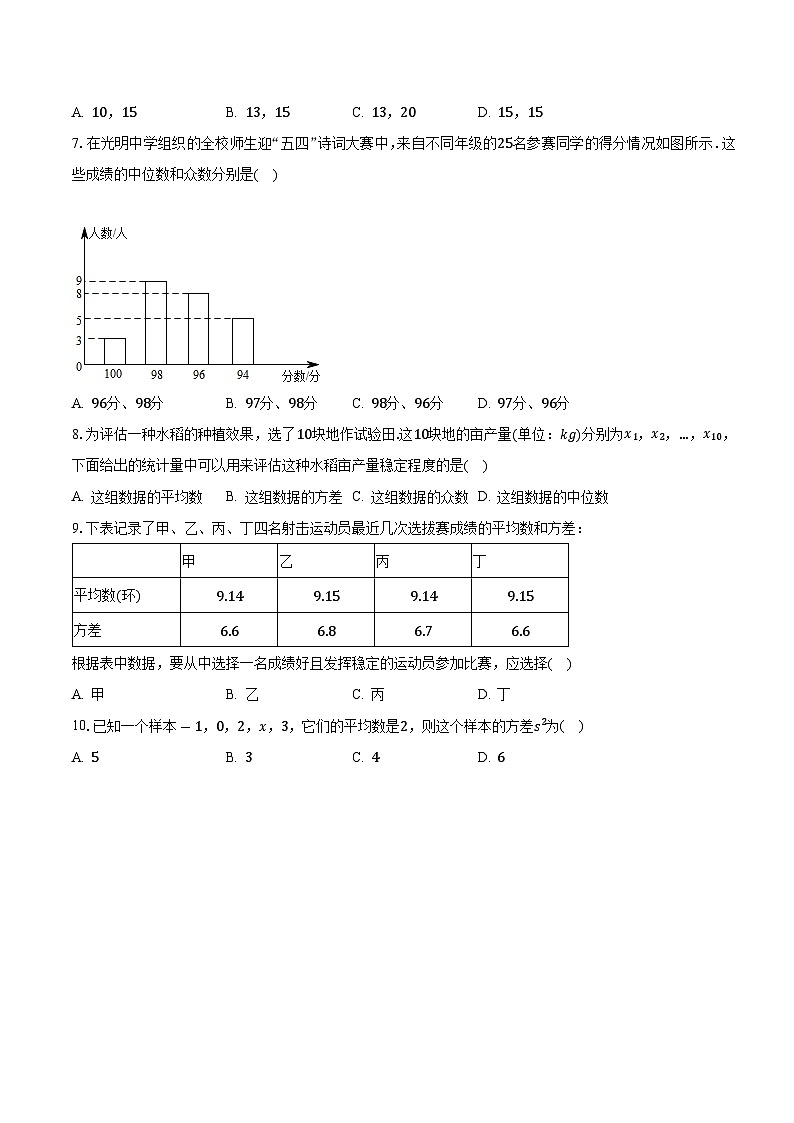
7.在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的名参赛同学的得分情况如图所示.这些成绩的中位数和众数分别是( )
A. 分、分 B. 分、分 C. 分、分 D. 分、分
8.为评估一种水稻的种植效果,选了块地作试验田这块地的亩产量单位:分别为,,,,下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是( )
A. 这组数据的平均数 B. 这组数据的方差 C. 这组数据的众数 D. 这组数据的中位数
9.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
| 甲 | 乙 | 丙 | 丁 |
平均数环 | ||||
方差 |
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A. 甲 B. 乙 C. 丙 D. 丁
10.已知一个样本,,,,,它们的平均数是,则这个样本的方差为( )
A. B. C. D.
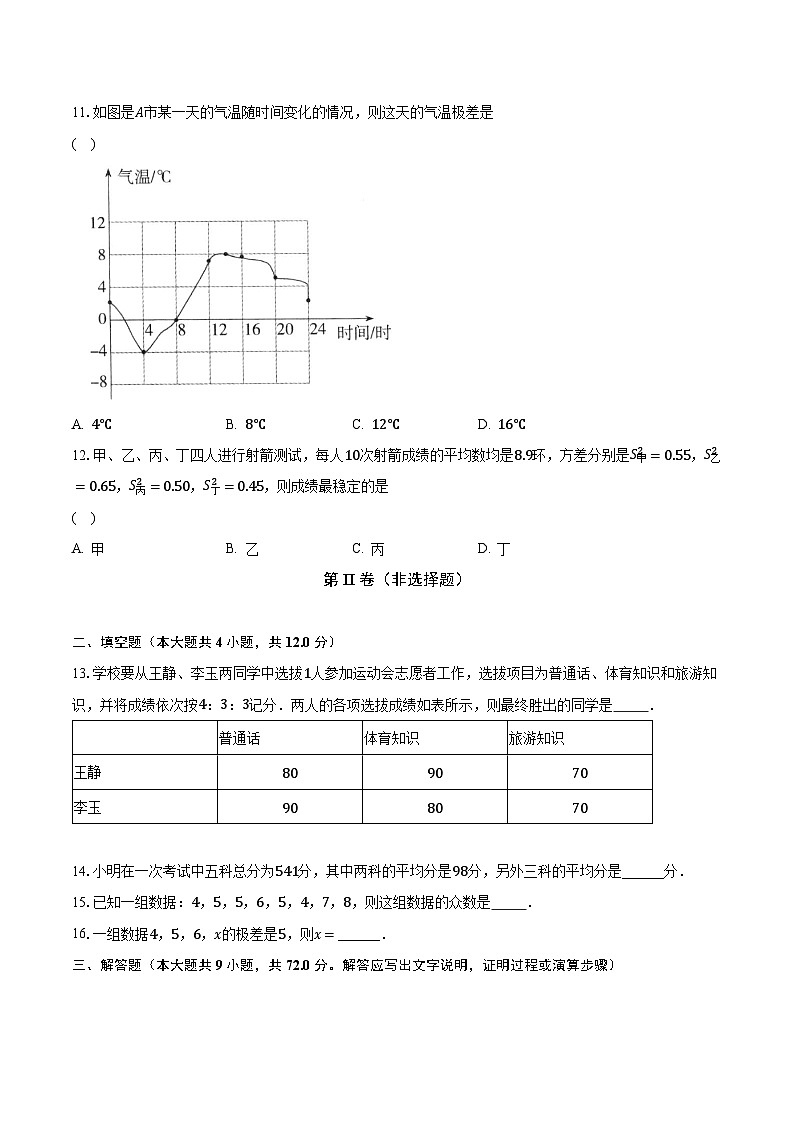
11.如图是市某一天的气温随时间变化的情况,则这天的气温极差是
( )
A. B. C. D.
12.甲、乙、丙、丁四人进行射箭测试,每人次射箭成绩的平均数均是环,方差分别是,,,,则成绩最稳定的是
( )
A. 甲 B. 乙 C. 丙 D. 丁
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13.学校要从王静、李玉两同学中选拔人参加运动会志愿者工作,选拔项目为普通话、体育知识和旅游知识,并将成绩依次按::记分.两人的各项选拔成绩如表所示,则最终胜出的同学是 .
| 普通话 | 体育知识 | 旅游知识 |
王静 | |||
李玉 |
14.小明在一次考试中五科总分为分,其中两科的平均分是分,另外三科的平均分是______分.
15.已知一组数据:,,,,,,,,则这组数据的众数是 .
16.一组数据,,,的极差是,则______.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17.本小题分
中国职业篮球赛的北京队和广东队在本赛季已进行了场比赛将比赛成绩进行统计后,绘制成统计图如图请完成以下问题:
在图中画出折线表示两队这场比赛成绩的变化情况.
已知北京队五场比赛的平均得分分,请你计算广东队五场比赛成绩的平均得分.
根据上述统计情况,试从平均得分、折线的走势、获胜场次三个方面分别进行简要分析,请预测下一场比赛哪个队更能取得好成绩?
18.本小题分
为激发学生探索宇宙的好奇心某校组织了“中国梦航天情”系列活动,如表是八年级班王磊同学在此次活动中各项目的成绩单位:分:
项目 | 知识竞赛 | 演讲比赛 | 版面创作 |
得分 |
若把知识竞赛、演讲比赛、版面创作三项成绩按照::的比例计入综合成绩,请计算王磊的综合成绩.
19.本小题分
某校为了评估甲、乙两个班的综合情况,对行规、学风、纪律三个项目进行评分,甲、乙两个班的得分情况单位:分如表:
| 行规 | 学风 | 纪律 |
甲班 | |||
乙班 |
若根据三项得分的平均数从高到低确定名次,那么两个班级的排名顺序怎样?
若“行规”“学风”“纪律”三个项目在总分中所占的比例分别为,,,则两个班级的排名顺序又怎样?
20.本小题分
端午节是中国的传统节日,民间有端午节吃粽子的习俗在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按分制进行评分,成绩单位:分均为不低于的整数为了解这次活动的效果,现从这两个年级各随机抽取名学生的活动成绩作为样本进行整理,并绘制统计图表,部分信息如下:
八年级名学生活动成绩统计表
成绩分 | |||||
人数 |
已知八年级名学生活动成绩的中位数为分.
请根据以上信息,完成下列问题:
样本中,七年级活动成绩为分的学生数是______ ,七年级活动成绩的众数为______ 分;
______ , ______ ;
若认定活动成绩不低于分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
21.本小题分
又到了一年一度的教师招聘期.某学校计划招聘两名数学教师,采取了“笔试面试”的招聘方式,笔试与面试的成绩满分均为分,根据规定,笔试成绩和面试成绩分别按一定的百分数折算成综合成绩综合成绩满分仍为分若参与应聘该校的六名应聘者的各项成绩如表所示:
类别 | ||||||
笔试成绩分 | ||||||
面试成绩分 | ||||||
综合成绩分 |
根据以上信息,解答下列问题:
直接写出这六名应聘者“面试成绩”的众数和中位数;
按照综合成绩排名录取前两名应聘者,最终录取的是谁?并说明理由.
22.本小题分
某校组织学生参加“防疫卫生知识竞赛”,为了了解某班学生在这次竞赛中的表现,现随机抽取该班名同学的竞赛成绩制表如下:
成绩 | |||||||
学生数 |
请根据表中信息,解答下列问题:
这名学生竞赛成绩的平均数是______ 分,中位数是______ 分;
甲、乙两人分别用样本的平均数和中位数来推断该班全体学生本次竞赛的情况,请你写出甲、乙两人的推断结论;
指出中谁的推断能较为合理地能反映出该班全体学生本次竞赛的真实水平,并说出另一个人的推断不合理的原因.
23.本小题分
“共抗疫情,爱国力行”,为加强抗击疫情的爱国主义教育宣传,某中学开展防疫知识线上竞赛活动,九年级、班各选出名选手参加竞赛,两个班选出的名选手的竞赛成绩如图所示.
请你计算两个班的平均成绩各是多少分.
写出两个班竞赛成绩的中位数,结合两班竞赛成绩的平均数和中位数,你认为哪个班的竞赛成绩较好.
计算两个班竞赛成绩的方差,并说明哪个班的成绩较为整齐.
24.本小题分
甲、乙两班各名同学参加“国防知识”比赛,其预赛成绩如下表:
成绩 | 分 | 分 | 分 | 分 | 分 |
甲班 | 人 | 人 | 人 | 人 | 人 |
乙班 | 人 | 人 | 人 | 人 | 人 |
填写下表:
| 平均数 | 中位数 | 众数 |
甲班 | ______ | ||
乙班 | ______ | ______ | 和 |
利用方差判断哪个班的成绩更加稳定?
25.本小题分
甲、乙两班各推选名同学进行投篮比赛,按照比赛规则,每人各投了个球,根据两个班选手的进球数,制作了如下统计图及数据分析表.
班级 | 平均数 | 中位数 | 众数 |
甲 | |||
乙 |
写出表格中,,的值: ______ , ______ , ______ ;
已知甲班选手进球数的方差为,求乙班选手进球数的方差;
如果要从这两个班中选出一个班参加学校的投篮比赛,你认为应该选择哪个班比较合适?为什么?
答案和解析
1.【答案】
【解析】解:,
故选:.
利用加权平均数的计算方法进行计算即可.
本题考查加权平均数的意义和计算方法,掌握计算方法是正确计算的前提.
2.【答案】
【解析】解:
.
3.【答案】
【解析】【分析】
本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法.
根据题意和加权平均数的计算方法,可以计算出这个人的最终得分.
【解答】
解:分,
即这个人的最终得分是分,
故选:.
4.【答案】
【解析】解:数据,,,,的众数为,
,
则这组数据为、、、、,
中位数为,
故选:.
根据众数的定义可得的值,再依据中位数的定义即可得答案.
本题考查众数与中位数的意义.中位数是将一组数据从小到大或从大到小重新排列后,最中间的那个数最中间两个数的平均数,叫做这组数据的中位数.众数是数据中出现最多的一个数.
5.【答案】
【解析】【分析】
此题考查了平均数和中位数,中位数的计算方法:如果数据的个数是奇数,则中间那个数据就是这群数据的中位数;如果数据的个数是偶数,则中间那个数据的算术平均值就是这群数据的中位数,根据平均数的计算公式和中位数的定义分别进行解答即可.
【解答】
解:这组数据的平均数是:;
把这组数据从小到大排列为:,,,,,最中间的数是,
则中位数是;
故选:.
6.【答案】
【解析】【解答】
解:把这组数据从小到大排列:、、、、,
最中间的数是,
则这组数据的中位数是;
出现了次,出现的次数最多,则众数是.
故选D.
【分析】
此题考查了中位数和众数,将一组数据从小到大或从大到小重新排列后,最中间的那个数或最中间两个数的平均数叫做这组数据的中位数;众数是一组数据中出现次数最多的数.
根据中位数和众数的定义分别进行解答即可.
7.【答案】
【解析】【分析】
本题考查众数,中位数,属于基础题.
利用众数和中位数的定义求解.
【解答】
解:出现了次,出现次数最多,
所以数据的众数为分;
共有个数,排序最中间的数为第数,是,
所以数据的中位数为分.
故选:.
8.【答案】
【解析】解:标准差,方差能反映数据的波动程度,
故选:.
根据平均数、众数和中位数及方差的意义求解即可.
本题主要考查统计量的选择,解题的关键是掌握平均数、众数和中位数及方差的意义.
9.【答案】
【解析】解:丁的平均数最大,方差最小,成绩最稳当,
所以选丁运动员参加比赛.
故选:.
利用平均数和方差的意义进行判断.
本题考查了方差:一组数据中各数据与它们的平均数的差的平方和的平均数,叫做这组数据的方差.方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
10.【答案】
【解析】解:平均数,
解得:,
方差.
故选:.
先由平均数的公式计算出的值,再根据方差的公式计算.
本题考查方差的定义:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
11.【答案】
【解析】从统计图中可以看出,这一天中最高气温是,最低气温是,
故这一天中最高气温与最低气温的差为,
故选 C.
12.【答案】
【解析】【分析】
本题考查方差的意义方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。根据方差是用来衡量一组数据波动大小的量,故由甲、乙、丙、丁的方差可作出判断.
【解答】
解:,,,,
,
成绩最稳定的是丁。
13.【答案】李玉
【解析】【分析】
本题考查了加权平均数的概念及求法,属于基础题,牢记加权平均数的计算公式是解题的关键.
根据不同的权计算每个人的得分即可作出比较.
【解答】
解:王静的成绩是:分,
李玉的成绩是:分,
,
最终胜出的同学是李玉.
故答案为:李玉.
14.【答案】
【解析】【分析】
此题主要考查了算术平均数的含义和求法,要熟练掌握,解答此题的关键是求出五科的总分是多少.首先根据题意,用其中两科的平均分乘以,求出它们的总分是多少,进而求出另外三科的总分是多少;然后根据平均数的求法,用另外三科的总分除以,求出另外三科的平均分是多少即可.
【解答】解:
分
另外三科的平均分是分.
故答案为.
15.【答案】
【解析】【分析】
本题主要考查众数,求一组数据的众数的方法:找出频数最多的那个数据,若几个数据的频数都是最多且相同,此时众数就是这多个数据.
根据众数的定义求解即可.
【解答】
解:这组数据中出现次,次数最多,所以这组数据的众数是.
故答案为:.
16.【答案】或
【解析】解:根据题意:或,
或.
故答案为:或.
根据极差的定义求解即可.注意分类讨论:为最大数或最小数.
此题考查了极差的知识,求极差的方法是用一组数据中的最大值减去最小值.此题要运用分类讨论的思想.
17.【答案】解:如图;
分;
从平均分看,两队的平均分相同,实力大体相当;
从折线的走势看,北京队比赛成绩呈上升趋势,而广东队比赛成绩呈下降趋势;
从获胜场数看,北京队胜三场,广东队胜两场,北京队成绩好;
综上,下一场比赛北京队更能取得好成绩.
【解析】在图中用描点法画出折线图;
由平均数的概念计算平均分;
从平均分、折线的走势、获胜场数三个方面分别进行简要分析,然后预测.
本题考查了平均数,折线图,熟练掌握平均数计算公式和折线图的意义是解题的关键.
18.【答案】解:分,
答:王磊的综合成绩为分.
【解析】根据加权平均数的定义计算即可得出答案.
本题主要考查加权平均数,解题的关键是掌握加权平均数的计算公式.
19.【答案】解:甲班算术平均数:分,
乙班的算术平均数:分,
因此第一名是乙班,第二名是甲班,
答:根据三项得分的平均数从高到低确定名次,乙班第一,甲班第二.
甲班的总评成绩:分,
乙班的总评成绩:分,
,
甲班高于乙班,
答:两个班级的排名顺序发生变化,甲班第一,乙班第二.
【解析】根据算术平均数的计算方法计算甲、乙班的平均数,通过比较得出得出结论,
利用加权平均数的计算方法分别计算甲、乙班的总评成绩,比较做出判断即可.
本题考查算术平均数、加权平均数的意义及计算方法,体会“权”在求平均数时的作用.
20.【答案】
【解析】解:由扇形统计图可得,成绩为分的人数为人,
成绩为分的人数为人,
成绩为分的人数为人,
则成绩为分的学生数为人,
出现次数最多的为分,
七年级活动成绩的众数为分,
故答案为:;;
由题意,将八年级的活动成绩从小到大排列后,它的中位数应是第个和第个数据的平均数,
八年级名学生活动成绩的中位数为分,
第个和第个数据的和为,
第个和第个数据分别为分,分,
成绩为分和分的人数为人,
成绩为分的人数为人,成绩为分的人数为人,
即,,
故答案为:;;
不是,理由如下:
结合中所求可得七年级的优秀率为,八年级的优秀率为,
七年级的平均成绩为分,八年级的平均成绩为分,
,,
本次活动中优秀率高的年级并不是平均成绩也高.
分别求得成绩为分,分,分的人数,再结合总人数为人列式计算即可求得成绩为分的学生数,然后根据众数定义即可求得众数;
根据中位数的定义将八年级的活动成绩从小到大排列,那么其中位数应是第个和第个数据的平均数,结合已知条件易得第个和第个数据分别为,,再根据表格中数据即可求得答案;
结合中所求,分别求得两个年级优秀率及平均成绩后进行比较即可.
本题主要考查众数,中位数及平均数,数据分析相关知识点是必考且重要知识点,必须熟练掌握,中根据中位数定义及已知条件确定第个和第个数据分别为分,分是解题的关键.
21.【答案】解:由题意可知,六名应聘者的面试成绩为分的出现次数最多,故众数为分,
将六名应聘者的面试成绩排好顺序为:、、、、、,中位数为分;
设笔试成绩为,面试成绩为,
,
解得,
,
笔试成绩占,面试成绩占.
应聘者的综合成绩为分,
应聘者的综合成绩为分,
综合成绩从高到底排序为:、、、、、,
最终录取的是和.
【解析】根据中位数和众数的定义即把这组数据从小到大排列,再找出最中间两个数的平均数就是中位数,再找出面试成绩中出现的次数最多的数即是众数;
设出笔试成绩和面试成绩的比,利用加权平均数的计算方法,列方程求出这个比,进而得出百分比,根据笔试成绩和面试成绩各占的百分比,分别求出六名应聘者的综合成绩,即可得出答案.
此题考查了加权平均数,用到的知识点是中位数、众数、加权平均数的计算公式,关键灵活运用有关知识列出算式.
22.【答案】
【解析】解:这名学生竞赛成绩的平均数是分,
将这名同学的竞赛成绩从小到大排列,处在中间位置的两个数的平均数为分,因此中位数是分,
故答案为:,;
甲:由样本平均数为分,估计该班全体学生本次竞赛的平均成绩大约为分,
乙:由样本中位数为分,估计该班全体学生本次竞赛大约有一半成绩超过分,约有一半的成绩不足分;
乙的推断比较科学合理.
由题意知样本中的名学生中,只有名学生的成绩在分以上,原因是该样本数据极差较大,所以平均数不能真实地反映实际情况.
求出各个数据之和,再除以数据个数即可得平均数;先把这些数据从小到大排列,只要找出最中间的两个数,即可得出中位数;
利用中位数、平均数的意义得出结论即可;
根据中位数、平均数所反映一组数据的整体情况进行判断即可.
本题考查中位数、平均数,掌握中位数、平均数的计算方法是解决问题的前提,理解平均数受极端值的影响是正确判断的关键.
23.【答案】解:九班的平均成绩是:分;
九班的平均成绩是:分;
九班的中位数是分,九班的中位数是分,
九班的平均成绩是分,九班的平均成绩是分,九班的中位数是分,九班的中位数是分,
九年级班竞赛成绩较好;
九班的成绩比较稳定,理由如下:
九班的方差是:,
九班的方差是:,
九班的方差小于八班的方差,
九班的成绩比较稳定.
【解析】根据算术平均数的概念求解可得;
根据中位数的定义即可得到结论;
先计算出两个班的方差,再根据方差的意义求解可得.
本题考查方差、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.
24.【答案】
【解析】解:根据题意可知,甲班预赛成绩的众数为:分;
乙班预赛成绩的平均数为:分,
中位数为:分.
填表如下:
| 平均数 | 中位数 | 众数 |
甲班 | |||
乙班 | 和 |
故答案为:,,;
甲班预赛成绩的方差为:,
乙班预赛成绩的方差为:,
从方差看,甲班的方差小,所以甲班的成绩更加稳定.
根据平均数和众数的概念求出甲的平均数与众数,根据方差的计算公式求出甲的方差;
先求出两个班成绩的方差,再根据方差的定义,方差越小数据越稳定即可解答.
本题考查的是方差、众数、中位数和平均数,掌握方差的计算公式、方差的性质是解题的关键.
25.【答案】
【解析】解:甲班名同学进球数从小到大排列为:、、、、、、、、、,出现的次数最多,
所以中位数,众数,
乙班名同学进球平均数为:个,
,
故答案为:,,;
乙班选手进球数的方差为:;
乙班,理由如下:
根据题意得:两个班成绩的平均数,中位数,众数相同,但甲班选手进球数的方差大于乙班选手进球数的方差,
乙班选手成绩更稳定,
应选乙班.
利用加权平均数、中位数和众数的定义直接求出;
根据方差的公式计算即可;
根据方差和个人发挥的最好成绩进行选择.
本题考查了平均数,中位数,众数和方差的意义,掌握相关知识是解题的关键.









