初中数学人教版九年级上册24.2.1 点和圆的位置关系备课课件ppt

这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系备课课件ppt，共33页。PPT课件主要包含了逐点学练，本节小结，作业提升，学习目标，本节要点，学习流程，感悟新知，知识点，点和圆的位置关系，r10等内容，欢迎下载使用。

点和圆的位置关系圆的确定三角形的外接圆反证法
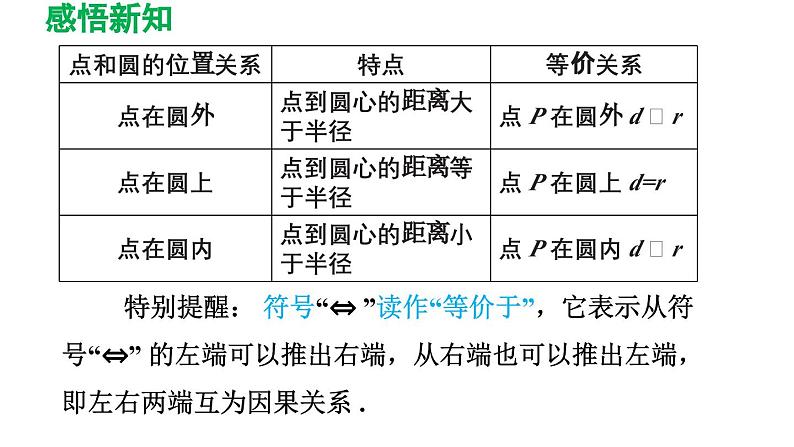
点和圆的位置关系设⊙ O 的半径为 r，点 P 到圆心的距离 OP=d，则有：
拓宽视野一个圆将平面分为三个部分：①圆的外部；②圆上；③圆的内部.
特别提醒： 符号“⇔ ”读作“等价于”，它表示从符号“⇔” 的左端可以推出右端，从右端也可以推出左端，即左右两端互为因果关系 .
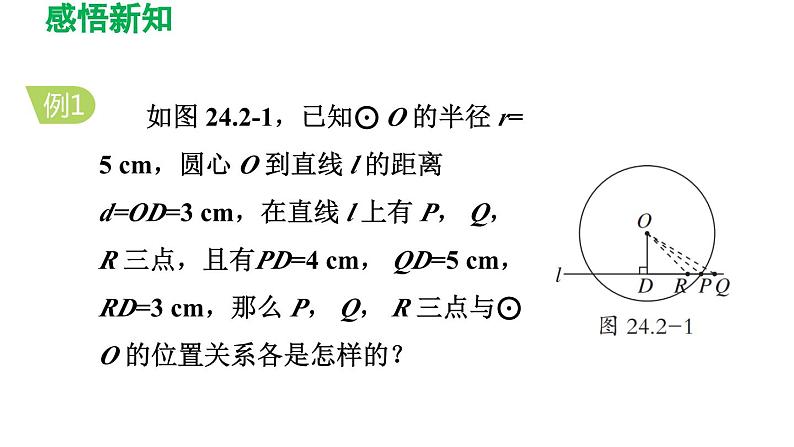
如图 24.2-1，已知⊙ O 的半径 r= 5 cm，圆心 O 到直线 l 的距离 d=OD=3 cm，在直线 l 上有 P， Q， R 三点，且有PD=4 cm， QD=5 cm， RD=3 cm，那么 P， Q， R 三点与⊙ O 的位置关系各是怎样的？
解题秘方：比较点到圆心的距离与半径的大小确定点的位置情况 .
1-1.在矩形 ABCD 中，AB=8， AD=6，以顶点D 为圆心作半径为 r 的圆，若要求另外三个顶点 A， B， C 中至少有一个点在圆内，且至少有一个点在圆外，则 r 的取值范围是_________ .
方法点拨过不在同一条直线上的任意四点作圆：要想过四点作圆，应先作出经过不在同一条直线上的三点的圆，若第四个点到圆心的距离等于半径，则第四个点在圆上，否则，第四个点不在圆上 .
2. 确定一个圆的条件(1)已知圆心、半径，可以确定一个圆 .(2)不在同一条直线上的三个点确定一个圆 .
“确定”是“有且只有”的意思.
如图 24.2－2， 点 A， B， C 在同一条直线上， 点 D在直线 AB 外，过这四个点中的任意三个点，能画圆的个数是( )A. 1 B. 2 C. 3 D. 4
解题秘方：紧扣两点：(1)四个点中取三个点的组数；(2)去掉三个点共线的组数 .
解：不在同一条直线上的三个点确定一个圆，在 A， B， C，D 四个点中任取三个点的情况共有四种：点 A， B， C；点 A，B， D；点 B， C， D；点 A， C， D. 因为点 A， B， C 在同一条直线上，所以过这三个点不能画圆 . 所以过这四个点中的任意三个点，能画圆的个数是 3.
特别提醒：1. 确定一个圆要具备两个关键点：(1)已知三个点，若已知两个点或一个点，都无法确定圆；(2)三个点不在同一条直线上 .2. 圆心为任意两条弦(不平行)的垂直平分线的交点 .
2-1.小明不慎把家里的圆形玻璃打碎了，其中四块如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块是( )A. ① B. ② C. ③ D. ④
1.三角形的外接圆 经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆，这个三角形叫做这个圆的内接三角形 .“接”是指三角形的三个顶点都在圆上 .
2. 三角形的外心 (1)定义： 三角形的外接圆的圆心是三角形三条边的垂直平分线的交点，叫做这个三角形的外心 .(2)性质： 三角形的外心到三角形三个顶点的距离相等，等于其外接圆的半径 .
3. 三角形外接圆的作法 (1)作三角形任意两边的垂直平分线，确定其交点；(2)以该交点为圆心，以交点到三个顶点中任意一点的距离为半径作圆即可 .
特别提醒三角形外心的位置：锐角三角形的外心在三角形的内部；直角三角形的外心是斜边的中点；钝角三角形的外心在三角形的外部.
如图 24.2－ 3， △ ABC 内接于⊙O， ∠ C=45 °，AB=4，求⊙ O 的半径 .
解题秘方：连接半径，利用圆周角与圆心角的关系结合勾股定理求解 .
3-1.若直角三角形的两条直角边长分别为 3，4，则直角三角形的外接圆的面积为 _____ (结果保留 π ) .
1.定义  假设命题的结论不成立，由此经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立，这种方法叫做反证法 .
2. 步骤 (1)假设命题的结论不成立，即假设结论的反面成立；(2)从这个假设出发，通过推理论证，得出矛盾；(3)由矛盾断定假设不正确，从而肯定原命题的结论成立.
警示误区1. 假设否定的是命题的结论，而不是已知条件 .2. 在推理论证时，要把假设作为新增条件参加论证 .
如图 24.2-4， AB， CD 是⊙ O 内非直径的两条弦 .求证： AB 与 CD 不能互相平分 .
解题秘方：利用垂径定理的推论结合垂线的唯一性证明 .
证明： 如图 24.2-4，设 AB， CD 交于点 P，连接 OP.假设 AB 与 CD 互相平分，则 CP=DP， AP=BP.∵ AB， CD 是⊙ O 内非直径的两条弦，∴ OP ⊥ AB， OP ⊥ CD.
这与“过一点有且只有一条直线与已知直线垂直”相矛盾，∴假设不成立 .∴ AB 与 CD 不能互相平分 .
4-1.用反证法证明 “ △ ABC 中至少有两个锐 角”， 第一步应为( )A. 假设△ ABC 中至多有一个锐角B. 假设△ ABC 中有一个直角C. 假设△ ABC 中有两个直角D. 假设△ ABC 中有两个锐角