

2021-2022学年湖北省武汉市青山区八年级(上)期中数学试卷(含答案)
展开
这是一份2021-2022学年湖北省武汉市青山区八年级(上)期中数学试卷(含答案),共27页。
2021-2022学年湖北省武汉市青山区八年级(上)期中数学试卷
一、你一定能选对!(本大题共有10小题,每小题3分,共30分)下列各题均有四个备选答案,其中有且只有一个是正确的,请将正确答案的代号在答题卡上将对应的答案标号涂黑.
1.(3分)下列品牌的标识中,是轴对称图形的是( )
A. B.
C. D.
2.(3分)下列图形中有稳定性的是( )
A.四边形 B.三角形 C.五边形 D.六边形
3.(3分)下列长度的三条线段能组成三角形的是( )
A.5,6,11 B.4,4,9 C.3,4,8 D.8,7,14
4.(3分)如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.62° B.72° C.76° D.66°
5.(3分)从n边形的一个顶点出发,可以作5条对角线,则n的值是( )
A.6 B.8 C.10 D.12
6.(3分)如图,△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,点E,若△ABC与△BCE的周长分别是36cm和22cm,则AD的长是( )
A.7cm B.8cm C.10cm D.14cm
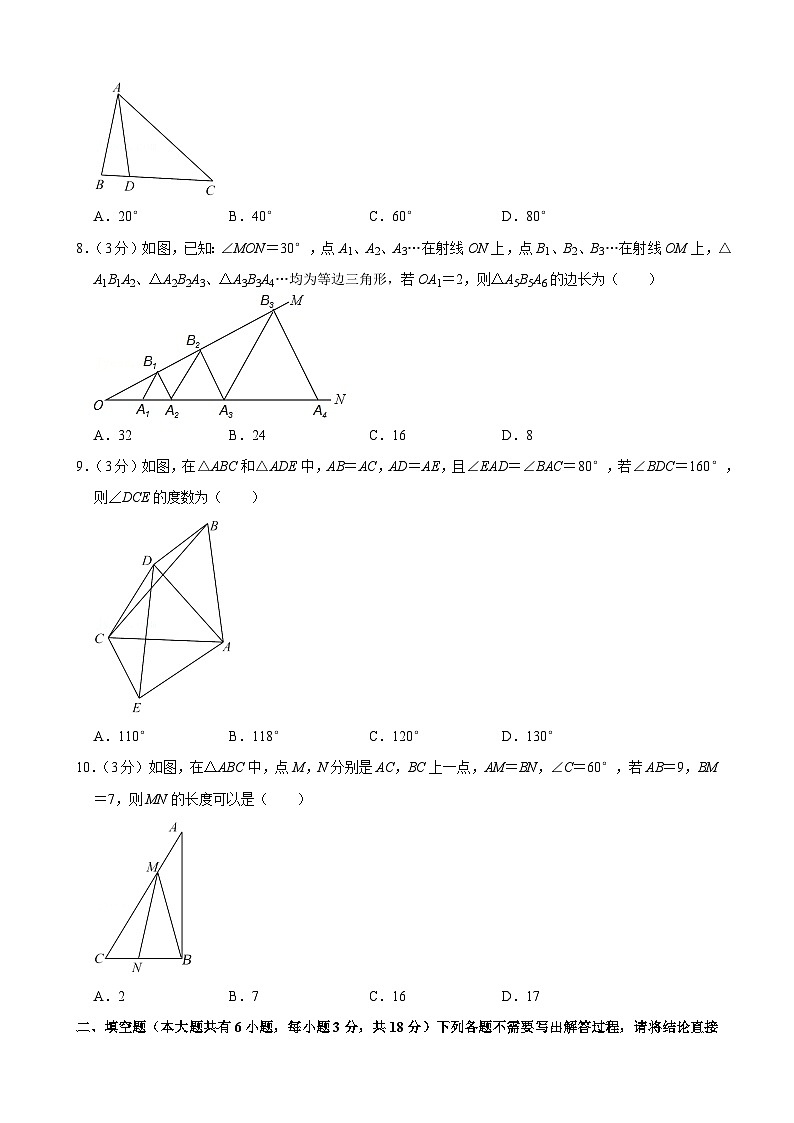
7.(3分)如图,△ABC中,AB=AD=DC,∠C=2∠BAD,则∠BAC的度数是( )
A.20° B.40° C.60° D.80°
8.(3分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
A.32 B.24 C.16 D.8
9.(3分)如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠EAD=∠BAC=80°,若∠BDC=160°,则∠DCE的度数为( )
A.110° B.118° C.120° D.130°
10.(3分)如图,在△ABC中,点M,N分别是AC,BC上一点,AM=BN,∠C=60°,若AB=9,BM=7,则MN的长度可以是( )
A.2 B.7 C.16 D.17
二、填空题(本大题共有6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结论直接填写在答题卷的指定位置.
11.(3分)点P(2,﹣5)关于x轴对称的点的坐标为 .
12.(3分)一个n边形的每个外角都等于72°,则n= .
13.(3分)用直尺和圆规作一个角等于已知角,如图,能得到△COD≌△C′O′D′的依据是 .
14.(3分)等腰△ABC的一个外角是100°,则其顶角的度数为 .
15.(3分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O,OF⊥AB于点F.下列结论:①∠EOB=60°;②BF+CD=BC;③AE+AD=2AF;④S四边形BEDC=2S△BOC+S△EDO.其中正确结论是 .
16.(3分)如图,在四边形ABCD中,AB=AC,DB平分∠ADC,∠BCD=150°.则∠ABD的度数为 °.
三、解下列各题(本大题共8小题,共72分)下列各题需要在答题卷的指定位置写出文字说明、证明过程、演算步骤或画出图形.
17.(8分)如图,DE分别与△ABC的边AB,AC交于点D,点E,与BC的延长线交于点F,∠B=65°,∠ACB=70°,∠AED=42°,求∠BDF的度数.
18.(8分)如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF,求证:AC∥DF.
19.(8分)已知一个三角形的三条边的长分别为:n+6;3n;n+2.(n为正整数)
(1)若这个三角形是等腰三角形,求它的三边的长;
(2)若这个三角形的三条边都不相等,且为正整数,直接写出n的最大值为 .
20.(8分)如图,六边形ABCDEF是正六边形,请用无刻度直尺画图,画图过程用虚线表示,画图结果用实线表示,按要求完成下列问题:
(1)如图1,连接AC.
①∠ACB= °;
②在图1中画出以AC为边的等边三角形,且另一个顶点在六边形的边上;
(2)已知,P为AF边上一点,
①如图2,在AB边上找一点Q,使得AQ=AP;
②如图3,在CD边上找一点H,使得PH⊥CD.
21.(8分)如图,在等边△ABC中,P为AB边上的一点,线段BC与DC关于直线CP对称,连接DA并延长交直线CP于点E.
(1)若∠ACE=20°,求∠CED的度数;
(2)若AE=1,CE=4.求AD的长.
22.(10分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,以BC为边向左作等边△BCE,点D为AB中点,连接CD,点P、Q分别为CE、CD上的动点.
(1)求证:△ADC为等边三角形;
(2)求PD+PQ+QE的最小值.
23.(10分)已知,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上一点,E为射线AD上一点,连接BE、CE.
(1)如图1,若∠ADC=60°,CE平分∠ACB.求证:BD=DE;
(2)若∠CED=45°.
①如图2,求证:BE⊥AE;
②如图3,若∠BED=30°,E在A、D之间,且AE=1,求BE的长.
24.(12分)已知,在平面直角坐标系中,A,B两点的坐标分别为点A(3,0),点B(0,b),将线段AB绕点A顺时针旋转α°得到AC,连接BC.
(1)若α=90.
①如图1,b=1,直接写出点C的坐标;
②如图2,D为BC中点,连接OD.求证:OD平分∠AOB;
(2)如图3,若α=60,b=3,N为BC边上一点,M为AB延长线上一点,BM=CN,连接MN,将线段MN绕点N逆时针旋转120°得到NP,连接OP.求当∠AOP取何值时,线段OP最短.
2021-2022学年湖北省武汉市青山区八年级(上)期中数学试卷
参考答案与试题解析
一、你一定能选对!(本大题共有10小题,每小题3分,共30分)下列各题均有四个备选答案,其中有且只有一个是正确的,请将正确答案的代号在答题卡上将对应的答案标号涂黑.
1.(3分)下列品牌的标识中,是轴对称图形的是( )
A. B.
C. D.
【解答】解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
故选:A.
2.(3分)下列图形中有稳定性的是( )
A.四边形 B.三角形 C.五边形 D.六边形
【解答】解:根据三角形具有稳定性,可得四个选项中只有三角形具有稳定性.
故选:B.
3.(3分)下列长度的三条线段能组成三角形的是( )
A.5,6,11 B.4,4,9 C.3,4,8 D.8,7,14
【解答】解:A.∵5+6=11,∴不能组成三角形,不符合题意;
B.∵4+4<9,∴不能组成三角形,不符合题意;
C.∵3+4<8,∴不能组成三角形,不符合题意;
D.∵8+7>14,∴能组成三角形,符合题意.
故选:D.
4.(3分)如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.62° B.72° C.76° D.66°
【解答】解:由三角形内角和定理得,∠2=180°﹣40°﹣64°=76°,
∵两个三角形全等,
∴∠1=∠2=76°,
故选:C.
5.(3分)从n边形的一个顶点出发,可以作5条对角线,则n的值是( )
A.6 B.8 C.10 D.12
【解答】解:设多边形有n条边,
则n﹣3=5,
解得n=8,
故选:B.
6.(3分)如图,△ABC中,AB的垂直平分线DE分别与边AB,AC交于点D,点E,若△ABC与△BCE的周长分别是36cm和22cm,则AD的长是( )
A.7cm B.8cm C.10cm D.14cm
【解答】解:∵DE是AB的垂直平分线,
∴EA=EB,AD=BD=12AB,
∵△EBC的周长是22cm,
∴BC+BE+EC=22cm,即AC+BC=22cm,
∵△ABC的周长是36cm,
∴AB+AC+BC=36cm,
∴AB=36﹣22=14(cm),
∴AD=12AB=12×14=7(cm).
故选:A.
7.(3分)如图,△ABC中,AB=AD=DC,∠C=2∠BAD,则∠BAC的度数是( )
A.20° B.40° C.60° D.80°
【解答】解:∵AD=DC,
∴∠C=∠DAC,
∴∠ADB=2∠C,
∵AB=AD,∠C=2∠BAD,
∴∠ABD=∠ADB=4∠BAD,
∵∠ABD+∠ADB+∠BAD=180°,
∴4∠BAD+∠4∠BAD+∠BAD=180°,
∴∠BAD=20°,
∴∠ABD=80°,∠C=40°,
∴∠BAC=180°﹣80°﹣40°=60°,
故选:C.
8.(3分)如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A5B5A6的边长为( )
A.32 B.24 C.16 D.8
【解答】解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∵∠MON=30°,
∴∠OB1A1=60°﹣30°=30°,
∴∠MON=∠OB1A1,
∴B1A1=OA1=2,
∴△A1B1A2的边长为2,
同理得:∠OB2A2=30°,
∴OA2=A2B2=OA1+A1A2=2+2=4,
∴△A2B2A3的边长为4,
同理可得:、△A3B3A4的边长为:23=8,
△A4B4A5的边长为:24=16,
则△A5B5A6的边长为:25=32,
故选:A.
9.(3分)如图,在△ABC和△ADE中,AB=AC,AD=AE,且∠EAD=∠BAC=80°,若∠BDC=160°,则∠DCE的度数为( )
A.110° B.118° C.120° D.130°
【解答】解:如图所示:
∵∠EAD=∠BAC=80°,
∴∠1=∠2,
在△BAD和△CAE中,
AB=AC∠1=∠2AD=AE,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠ABD,
∵∠BAC=80°,AB=AC,
∴∠BCA=∠CBA=50°,
∴∠DCE=∠4+∠BCA+∠ACE=∠4+50°+∠ABD=∠4+50°+∠3+∠ABC=∠3+∠4+100°,
又∵∠BDC=160°,
∴∠3+∠4=180°﹣∠BDC=20°,
∴∠DCE=20°+100°=120°,
故选:C.
10.(3分)如图,在△ABC中,点M,N分别是AC,BC上一点,AM=BN,∠C=60°,若AB=9,BM=7,则MN的长度可以是( )
A.2 B.7 C.16 D.17
【解答】解:如图,作等边△ABQ和等边△MBP,连接QP,QM,
在等边△ABQ和等边△MBP中,∠QBA=∠PBM=60°,
∴∠QBP+∠QBM=∠QBM+∠ABM=60°,
∴∠QBP=∠ABM,
又∵QB=AB=9,PB=MB=7,
∴△QBP≌△ABM(SAS),
∴∠BQP=∠BAM,PQ=AM,
∵AM=BN,
在△ABC中,∠ACB+∠CAB+∠CBA=180°,∠ACB=60°,
∴∠MBC=180°﹣60°﹣∠MAB﹣∠ABM=120°﹣∠MAB﹣∠ABM,
在△QBP中,∠QPB+∠BQP+∠QBP=180°,∠MPB=60°,
∴∠MPQ=180°﹣60°﹣∠BQP﹣∠QBP=120°﹣∠MAB﹣∠ABM,
∴∠MBN=MPQ,
在△QMP和△NMB中,
PB=MB∠MBN=∠MPQPQ=BN,
∴△QMP≌△NMB(SAS),
∴MQ=MN,
在△QMB中,QB﹣MB<QM<QB+MB,
∴AB﹣MB<MN<AB+MB,
∴2<MN<16,
∴选项B,MN=7符合题意,
故选:B.
二、填空题(本大题共有6小题,每小题3分,共18分)下列各题不需要写出解答过程,请将结论直接填写在答题卷的指定位置.
11.(3分)点P(2,﹣5)关于x轴对称的点的坐标为 (2,5) .
【解答】解:点P(2,﹣5)关于x轴对称的点的坐标为:(2,5),
故答案为:(2,5).
12.(3分)一个n边形的每个外角都等于72°,则n= 5 .
【解答】解:∵n边形的每个外角都相等,
∴这个n边形是正多边形,
∵多边形的外角和为360°,
∴多边形的边数为360°÷72°=5.
故答案为:5.
13.(3分)用直尺和圆规作一个角等于已知角,如图,能得到△COD≌△C′O′D′的依据是 SSS .
【解答】解:由作法得OD=OC=OD′=OC′,CD=C′D′,
所以△COD≌△C′O′D′(SSS).
故答案为SSS.
14.(3分)等腰△ABC的一个外角是100°,则其顶角的度数为 20°或80° .
【解答】解:∵等腰△ABC的一个外角是100°,
∴①当顶角的外角是100°,
∴顶角等于180°﹣100°=80°,
②当底角的外角是100°,
∴底角等于180°﹣100°=80°,
∴顶角等于180°﹣80°﹣80°=20°,
∴其顶角的度数为:20°或80°.
故答案为:20°或80°.
15.(3分)如图,在△ABC中,∠A=60°,角平分线BD,CE交于点O,OF⊥AB于点F.下列结论:①∠EOB=60°;②BF+CD=BC;③AE+AD=2AF;④S四边形BEDC=2S△BOC+S△EDO.其中正确结论是 ①③④ .
【解答】解:如图1,∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BD、CE分别平分∠ABC、∠ACB,且BD、CE相交于点O,
∴∠OBC=∠OBA=12∠ABC,∠OCB=∠OCA=12∠ACB,
∴∠OBC+∠OCB=12(∠ABC+∠ACB)=60°,
∴∠EOB=∠OBC+∠OCB=60°,
故①正确;
如图2,在BC上截取BM=BE,连接OM,
在△BOE和△BOM中,
BE=BM∠OBE=∠OBMOB=OB,
∴△BOE≌△BOM(SAS),
∴OE=OM,∠EOB=∠BOM=60°,
∵∠COD=∠EOB=60°,
∴∠COM=180°﹣∠BOM﹣∠COD=60°,
∴∠COD=∠COM,
在△COD和△COM中,
∠COD=∠COMOC=OC∠OCD=∠OCM,
∴△COD≌△COM{ASA),
∴CD=CM,
∴BE+CD=BC,
故②错误;
如图3,作OH⊥AC于点H,OG⊥BC于点G,连接OA,
∵OF⊥AB于点F,
∴∠AFO=∠AHO=90°,∠OFE=∠OHD=90°,
∵OF=OG,OH=OG,
∴OF=OH,
在Rt△AOF和Rt△AOH中,
OA=OAOF=OH,
∴Rt△AOF≌Rt△AOH(HL),
∴AF=AH,
∵∠EAC=∠COD=60°,
∴∠EAC+∠ACE=∠COD+∠ACE,
∵∠OEF=∠EAC+∠ACE,∠ODH=∠COD+∠ACE,
∴∠OEF=∠ODH,
在△OEF和△ODH中,
∠OEF=∠ODH∠OFE=∠OHDOF=OH,
∴△OEF≌△ODH(AAS),
∴EF=DH,
∴AE+AD=AE+AH+DH=AE+AH+EF=AF+AH=2AF,
故③正确;
如图2,∵△BOE≌△BOM,△COD≌△COM,
∴S△BOE=S△BOM,S△COD=S△COM,
∴S△BOE+S△COD=S△BOM+S△COM,=S△BOC,
∴S四边形BEDC=S△BOC+S△BOE+S△COD+S△EDO=2S△BOC+S△EDO,
故④正确,
故答案为:①③④.
16.(3分)如图,在四边形ABCD中,AB=AC,DB平分∠ADC,∠BCD=150°.则∠ABD的度数为 30 °.
【解答】解:作△BCD的外接圆⊙O,连接OA,OB,OC,OD,如图,
∵∠BCD=150°,
∴∠BOD=60°.
∵OB=OD,
∴△OBD为等边三角形.
∴∠OBD=∠ODB=60°,BD=OB=OD.
在△OBA和△OCA中,
OA=OAOB=OCAB=AC,
∴△OBA≌△OCA(SSS).
∴∠BOA=∠COA=12∠BOC.
∵DB平分∠ADC,
∴∠ADB=∠CDB=12∠ADC.
∵∠BDC=12∠BOC,
∴∠BOA=∠COA=∠ADB=∠CDB.
∵∠BOD=∠BDO=60°,
∴∠BOD﹣∠BOA=∠BDO﹣∠ADB.
∴∠AOD=∠ADO.
∴AO=AD.
在△OBA和△DBA中,
OB=BDBA=BAAO=AD,
∴△OBA≌△DBA(SSS).
∴∠ABO=∠ABD=12∠OBD=30°.
故答案为:30.
三、解下列各题(本大题共8小题,共72分)下列各题需要在答题卷的指定位置写出文字说明、证明过程、演算步骤或画出图形.
17.(8分)如图,DE分别与△ABC的边AB,AC交于点D,点E,与BC的延长线交于点F,∠B=65°,∠ACB=70°,∠AED=42°,求∠BDF的度数.
【解答】解:∵∠B=65°,∠ACB=70°,
∴∠A=180°﹣∠B﹣∠ACB
=180°﹣65°﹣70°
=45°,
又∵∠AED=42°,
∴∠BDF=∠A+∠AED
=45°+42°
=87°.
18.(8分)如图,点B,E,C,F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF,求证:AC∥DF.
【解答】证明:∵BE=CF(已知),
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
∠A=∠D∠B=∠DEFBC=EF,
∴△ABC≌△DEF(AAS),
∴AC=DF(全等三角形对应边相等).
19.(8分)已知一个三角形的三条边的长分别为:n+6;3n;n+2.(n为正整数)
(1)若这个三角形是等腰三角形,求它的三边的长;
(2)若这个三角形的三条边都不相等,且为正整数,直接写出n的最大值为 7 .
【解答】解:(1)①如果n+2=3n,
解得n=1,
三角形三边的长为3,3,7,不符合三角形三边关系;
②如果n+6=3n,
解得n=3,
三角形三边的长为5,9,9,符合三角形三边关系.
综上所述,等腰三角形三边的长为5,9,9;
(2)n的最大值为7.
由三角形三边关系知,(n+2)+(n+6)>3n(n+2)+3n>n+6,
解得43<n<8,
∵三角形的三条边都不相等,
∴3n≠n+6,
∴n≠3,
∴43<n<8且n≠3,
∵n为正整数,
∴n的最大值为7.
故答案为:7.
20.(8分)如图,六边形ABCDEF是正六边形,请用无刻度直尺画图,画图过程用虚线表示,画图结果用实线表示,按要求完成下列问题:
(1)如图1,连接AC.
①∠ACB= 30 °;
②在图1中画出以AC为边的等边三角形,且另一个顶点在六边形的边上;
(2)已知,P为AF边上一点,
①如图2,在AB边上找一点Q,使得AQ=AP;
②如图3,在CD边上找一点H,使得PH⊥CD.
【解答】解:(1)①∵六边形ABCDEF是正六边形,
∴∠ABC=120°,BA=BC,
∴∠ACB=∠BAC=12(180°﹣120°)=30°,
故答案为:30;
②如图1中,△ACE即为所求;
(2)①如图2中,点Q即为所求;
②如图3中,线段PH即为所求.
21.(8分)如图,在等边△ABC中,P为AB边上的一点,线段BC与DC关于直线CP对称,连接DA并延长交直线CP于点E.
(1)若∠ACE=20°,求∠CED的度数;
(2)若AE=1,CE=4.求AD的长.
【解答】解:(1)∵△ABC是等边三角形,
∴∠ACB=60°,CB=CA,
∵∠ACE=20°,
∴∠ECB=60°﹣20°=40°,
由翻折的性质可知,CB=CD,∠ECB=∠ECD=40°,
∴CA=CD,∠ACD=40°﹣20°=20°,
∴∠CAD=∠D=80°,
∵∠DAC=∠CED+∠ACE,
∴∠CED=80°﹣20°=60°.
(2)过点C作CT⊥DE于T.设∠ECA=α,则∠ECB=∠ECD=60°﹣α,
∴∠ACD=60°﹣2α,
∵CA=CD,
∴∠CAD=12(180°﹣60°+2α)=60°+α,
∵∠DAC=∠E+∠ACE,
∴∠E=60°+α﹣α=60°,
∵CT⊥AD,CA=CD,
∴AT=DT,
∴∠ECT=30°,
∴ET=12EC=2,
∴AT=DT﹣AE=2﹣1=1,
∴AD=2AT=2.
22.(10分)如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,以BC为边向左作等边△BCE,点D为AB中点,连接CD,点P、Q分别为CE、CD上的动点.
(1)求证:△ADC为等边三角形;
(2)求PD+PQ+QE的最小值.
【解答】(1)证明:∵ACB=90°,点D为AB的中点,
∴CD=AD,
∵∠ABC=30°,
∴∠A=60°,
∴△ABC是等边三角形;
(2)解:连接AP,BQ,
∵△BCE是等边三角形,
∴∠BCE=60°,
∴∠ACE=30°,
∵△ACD是等边三角形,
∴CP垂直平分AD,
∴DP=AP,
同理得EQ=BQ,
∴PD+PQ+QE=AP+PQ+BQ,
∴当点P、Q落在AB上时,PD+PQ+QE的最小值为AB,
∵∠ABC=30°,AC=2,
∴AB=2AC=4,
∴PD+PQ+QE的最小值为4.
23.(10分)已知,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上一点,E为射线AD上一点,连接BE、CE.
(1)如图1,若∠ADC=60°,CE平分∠ACB.求证:BD=DE;
(2)若∠CED=45°.
①如图2,求证:BE⊥AE;
②如图3,若∠BED=30°,E在A、D之间,且AE=1,求BE的长.
【解答】(1)证明:如图1中,延长CE交AB于点J.
∵CA=CB,∠ACB=90°,
∴∠CBA=∠CAB=45°,
∵CE平分∠ACB,
∴CJ⊥AB,AJ=JB,
∴EA=EB,
∵∠ADC=60°,
∴∠DAC=90°﹣∠ADC=30°,
∴∠EAB=∠EBA=15°,
∴∠EBD=30°,
∵∠EDC=∠EBD+∠BED=60°,
∴∠EBD=∠BED=30°,
∴DB=DE;
(2)①证明:如图2中,过点C作CH⊥CE交AE于点H.
∵∠AEC=45°,∠ECH=90°,
∴∠CEH=∠CHE=45°,
∴CE=CH,
∵∠ACB=∠ECH=90°,
∴∠ACH=∠BCE,
在△ACH和△BCE中,
CA=CB∠ACH=∠BCECH=CE,
∴△ACH≌△BCE(SAS),
∴∠CAH=∠CBE,
∵∠ADC=∠BDE,
∴∠ACD=∠BED=90°;
②解:如图3中,过点C作CH⊥CE交AD的延长线于点H,连接BH.
同法可证,△ACE≌△BCH(SAS),BH⊥AH,
∴BH=AE=1,
∵∠BHE=90°,∠BEH=30°,
∴BE=2BH=2.
24.(12分)已知,在平面直角坐标系中,A,B两点的坐标分别为点A(3,0),点B(0,b),将线段AB绕点A顺时针旋转α°得到AC,连接BC.
(1)若α=90.
①如图1,b=1,直接写出点C的坐标;
②如图2,D为BC中点,连接OD.求证:OD平分∠AOB;
(2)如图3,若α=60,b=3,N为BC边上一点,M为AB延长线上一点,BM=CN,连接MN,将线段MN绕点N逆时针旋转120°得到NP,连接OP.求当∠AOP取何值时,线段OP最短.
【解答】(1)①解:如图1中,过点C作CH⊥x轴于点H.
∵∠AOB=∠BAC=∠AHC=90°,
∴∠BAO+∠CAH=90°,∠CAH+∠ACH=90°,
∴∠OAB=∠ACH,
在△AOB和△CHA中,
∠AOB=∠CHA∠OAB=∠HCAAB=CA,
∴△AOB≌△CHA(AAS),
∴OB=AH,CH=OA,
∵B(0,1),A(3,0),
∴OB=1,OA=3,
∴AH=1,CH=3,OH=4,
∴C(4,3);
②证明:如图2中,过点D作DM⊥OA于点M,DN⊥OB于点N.
∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥BC,AD=DB=DC,∠DAB=∠DAC=45°,
∵∠DMO=∠DNO=∠MON=90°,
∴∠MDN=∠ADB=90°,
∴∠BDN=∠ADM,
∵∠ADB=∠AOB=90°,
∴∠DAM+∠DBO=180°,
∵∠DBO+∠DBN=180°,
∴∠DBN=∠DAM,
在△DNB和△DMA中,
∠DNB=∠DMA∠DBN=∠DAMDB=DA,
∴△DNB≌△DMA(AAS),
∴DM=DN,
∵DM⊥OA,DN⊥OB,
∴OD平分∠AOB;
(2)解:作NE∥AB交AC于点E,连接PM,AN,PA,过点O作OF⊥PA交PA的延长线于点F.
∵OA=OB,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵△ABC是等边三角形,
∴∠CBA=∠CAB=∠C=60°,
∵NE∥AB,
∴∠CNE=∠CBA=60°,∠CEN=∠CAB=60°,
∴△CEN是等边三角形,
∴CN=NE=CE,
∵BM=CN,CB=CA,
∴NE=BM,BN=AE,
∵∠CBA=∠CEN=60°,
∴∠MBN=∠AEN=120°,
在△NBM和△AEN中,
BM=EN∠NBM=∠NEABN=EA,
∴△NBM≌△AEN(SAS),
∴NM=AN,
∵NM=NP,
∴AN=NP,
∴∠NMA=∠NAM,∠NAP=∠NPA,
∵∠MNP=120°,
∴2∠NAM+2∠NAP=240°,
∴∠PAM=∠NAM+∠NAP=120°,
∴∠OAP=∠OAB+∠MAP=165°,
∴∠AOF=180°﹣165°=15°,
∴点P在直线PA上运动(∠OAP=165°),
根据垂线段最短可知,当点P与F重合时,OP的值最小,此时∠AOP=90°﹣15°=75°.
相关试卷
这是一份2021-2022学年湖北省武汉市青山区八年级(上)期中数学试卷,共27页。
这是一份2021-2022学年湖北省武汉市青山区八年级(上)期末数学试卷,共21页。
这是一份2020-2021学年湖北省武汉市青山区八年级(下)期中数学试卷,共25页。









