江西省赣州市寻乌县2022届九年级上学期期末检测数学试卷(含解析)

这是一份江西省赣州市寻乌县2022届九年级上学期期末检测数学试卷(含解析)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
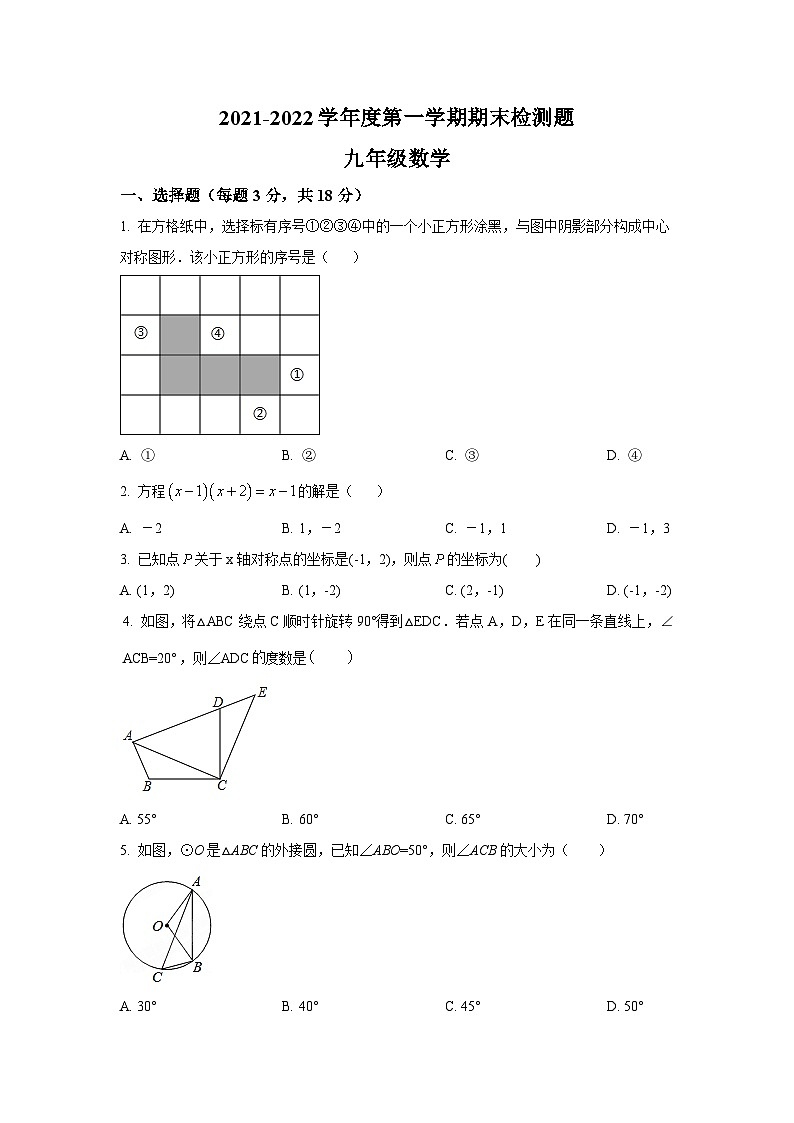
2021-2022学年度第一学期期末检测题九年级数学一、选择题（每题3分，共18分）1. 在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形．该小正方形的序号是（    ）A. ① B. ② C. ③ D. ④2. 方程的解是（    ）A. －2 B. 1，－2 C. －1，1 D. －1，33. 已知点关于x轴对称点的坐标是(-1，2)，则点的坐标为(     )A. (1，2) B. (1，-2) C. (2，-1) D. (-1，-2)4. 如图，将△ABC绕点C顺时针旋转90°得到△EDC．若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC度数是　　A. 55° B. 60° C. 65° D. 70°5. 如图，⊙O是△ABC的外接圆，已知∠ABO=50°，则∠ACB的大小为（　　）A. 30° B. 40° C. 45° D. 50°6. 已知二次函数的图象与x轴交于点与，其中，方程的两根为m，n（m<n），则下列判断正确的是（    ）A.  B.  C.  D. 二、填空题（每题3分，共18分）7. “清明时节雨纷纷”是_______事件．(填“必然”“不可能”或“随机”)8. 抛物线的对称轴是直线______．9. 已知圆锥的母线长为10，侧面积为，则其侧面展开图的圆心角度数为________度．10. 已知α、β是一元二次方程x2-2021x+2020=0的两实根，则代数式(α-2021)(β-2021)=___．11. 如图，在中，直径，弦于，若，则____12. 如图，已知⊙P的半径是1，圆心P在抛物线上运动，当⊙P与x轴相切时，圆心P的坐标为_____．三、解答题（每题6分，共30分）13. （1）解方程：（2）如图，在△ABC中，已知∠ABC＝30°，将△ABC绕点B逆时针旋转50°后得到，若∠A＝100°，求证：．14 先化简，再求值：，其中实数m可使关于x的一元二次方程x2﹣4x﹣m＝0有两个相等的实数根．15. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连接AC，BC．（1）求证：∠A＝∠BCD；（2）若AB＝10，CD＝6，求BE的长．16. 某同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，分别用、、表示；田赛项目：跳远，跳高分别用、表示．该同学从5个项目中任选一个，恰好是田赛项目的概率为______；该同学从5个项目中任选两个，利用树状图或表格列举出所有可能出现的结果，并求恰好是一个田赛项目和一个径赛项目的概率．17. 等腰△ABC中，，以AB为直径作圆交BC于点D，请仅用无刻度的直尺．根据下列条件分别在图1、图2中画一条弦，使这条弦的长度等于弦BD．（保留作图痕迹，不写作法，用虚线表示画图过程，实线表示画图结果）（1）如图1，；（2）如图2，四、解答题（每题8分，共24分）18. 在平面直角坐标系中，△ABC位置如图所示．（每个小方格都是边长为1个单位长度的正方形）
 （1）画出△ABC关于原点对称的；（2）将绕点C′顺时针旋转90°，画出旋转后得到的，并直接写出此过程中点A′运动的路径长度．（结果保留π）19. 如图1，在Rt△ABC中，D为AB的中点，P是BC边上一动点，连接PD，PA．若BC＝4，AC＝3，设PC＝x（当点P与点C重合时，x的值为0），．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整．（1）通过取点、画图、计算，得到了x与y几组值，如下表：x00.511.522.533.54y5.55.15 4.945.15.5 6.77.5说明：补全表格时，相关数值保留一位小数．（参考数据：，，）．（2）如图2，描出剩余的点，并用光滑的曲线画出该函数的图象．（3）观察图象，下列结论正确的有______．①函数有最小值，没有最大值              ②函数有最小值，也有最大值③当时，y随着x的增大而增大        ④当y>5.5时，x的取值范围是x>2.520. 某超市对进货价位元/千克的某种苹果的销售情况进行统计，发现每天销售量（千克）与销售价（元/千克）存在一次函数关系，如图所示．（1）求关于的函数关系式（不要求写出的取值范围）；（2）应怎样确定销售价，使该品种苹果的每天销售利润最大？最大利润是多少？五、解答题（每题9分，共18分）21. 如图，在△ABC中，AB＝AC，点D在BC上，BD＝DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．（1）证明：AB是⊙O的直径（2）试判断DE与⊙O的位置关系，并说明理由；（3）若DE的长为3，∠BAC＝60°，求⊙O的半径．22. 通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．（1）思路梳理∵AB=CD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．∵∠ADC=∠B=90°，∴∠FDG=180°，点F、D、G共线．根据　　　　，易证△AFG≌　　　　，得EF=BE+DF．（2）类比引申如图2，四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系　　　　时，仍有EF=BE+DF．（3）联想拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．六、解答题（共12分）23. 已知抛物线与x轴只有一个公共点．（1）若抛物线过点，求的最小值；（2）已知点中恰有两点在抛物线上．①求抛物线解析式；②设直线l：与抛物线交于M，N两点，点A在直线上，且，过点A且与x轴垂直的直线分别交抛物线和直线l于点B，C．求证：与的面积相等．
 
答案 1. B解：如图，把标有序号②的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形，
故选B．2. C∵∴∴∴或∴，故选：C．3. D根据平面直角坐标系中两个关于坐标轴成轴对称的点的坐标特点，∴点关于x轴对称点的坐标是(-1，2)，则点的坐标为（-1，-2）．故选：D．4. C∵将△ABC绕点C顺时针旋转90°得到△EDC．∴∠DCE=∠ACB=20°，∠BCD=∠ACE=90°，AC=CE，∴∠ACD=90°-20°=70°，∵点A，D，E在同一条直线上，∴∠ADC+∠EDC=180°，∵∠EDC+∠E+∠DCE=180°，∴∠ADC=∠E+20°，∵∠ACE=90°，AC=CE∴∠DAC+∠E=90°，∠E=∠DAC=45°在△ADC中，∠ADC+∠DAC+∠DCA=180°，即45°+70°+∠ADC=180°，解得：∠ADC=65°，故选C．5. B解：△AOB中，OA=OB，∠ABO=50°，
∴∠AOB=180°-2∠ABO=80°，故选B．6. DA：两函数的对称轴不变所以n＞，选项说法错误不符合题意；B：方程有根所以＞0，选项说法错误不符合题意；C：，选项说法错误不符合题意；D：a＞0时，开口向上图象向下平移；a＜0时，开口向下图象向上平移，选项说法正确符合题意．故答案选：D7. 随机“清明时节雨纷纷”这一事件可能发生，也可能不发生，因此这个事件是随机事件，故答案为随机.8. x＝1解：抛物线，该抛物线的对称轴是直线，故答案是：．9. 108圆锥的侧面展开图是一个扇形，扇形所在圆的半径为圆锥的母线长设圆锥的侧面展开图的圆心角度数为度则，即解得故答案为：108．10. 2020解：∵α、β是一元二次方程x2-2021x+2020=0的两实根，∴α+β=2021，αβ=2020，∴（α-2021）（β-2021）=αβ-2021（α+β）+20212=2020-2021×2021+20212=2020．故答案为：2020．11. 由圆周角定理得，∠COB=2∠A=60°，∴CE=OC•sin∠COE=2×=，∵AE⊥CD，∴CD=2CE=2，故答案为2.12. （3，1）或（﹣1，1）或（1，﹣1）解：设点P（x，y），，∵⊙P与x轴相切∴|y|＝1∴y＝±1①当y＝1时，，解得：x1＝3，x2＝－1∴点P（3，1），（－1，1）②当y＝－1时，，解得：x＝1∴点P（1，－1）故答案为（3，1）或（－1，1）或（1，－1）13. （1）解： 或 所以  或（2）证明：∵∠ABC＝30°，∠A＝100°，∴∠C＝50°．∵△ABC绕点B逆时针旋转50°后得到，∴，，∴，∴．14.解：＝•＝∵一元二次方程x2﹣4x﹣m＝0有两个相等的实数根，∴△＝b2﹣4ac＝16+4m＝0，∴m＝﹣4将m＝﹣4代入原式＝＝＝．15. (1)∵直径AB⊥弦CD，∴,∴∠A=∠BCD；(2)连接OC，∵直径AB⊥弦CD，CD=6，∴CE=ED=3，∵直径AB=10，∴CO=OB=5，在Rt△COE中，∵OC=5，CE=3，∴OE==4，∴BE=OB﹣OE=5﹣4=1．16. （1）∵5个项目中田赛项目有2个，∴该同学从5个项目中任选一个，恰好是田赛项目的概率为：．故答案为；（2）画树状图得：∵共有20种等可能的结果，恰好是一个田赛项目和一个径赛项目的有12种情况，∴恰好是一个田赛项目和一个径赛项目的概率为：．17. 解：（1）如图1，DE为所作：（2）如图2，DE为所作：18. （1）如图所示，即为所求（2）如图所示，即为所求∵，∴点A′运动的路径长为．
19. （1）如图1，取BC中点H，连接DH∵点D、H分别为AB、BC的中点∴，且DH为△BAC的中位线∴DH∥AC且， 又∵AC⊥BC∴DH⊥BC当PC＝x＝1时，∴，∴当PC＝x＝1时，同理可得故答案为：5.0；6.0．（2）描点绘制函数图像如图2所示：（3）由函数图像可知，函数有最小值，也有最大值，故①错误，②正确；由函数图像并结合表格中数据可知，函数图像最低点近似在x=1.25处，所以当时，y随着x的增大而增大，故③正确；当y>5.5时，x的取值范围是2.5<x≤4，故④错误；故答案为：②③．20. （1）设y=kx+b，由图象可知，，
解得：，则y=-4x+160;（2）设销售利润为P，根据题意，
得：P=（x-20）（-4x+160）
=-4x2+240x-3200，
=-4（x-30）2+400，
则当x=30时，P最大值=400，
答：当售价为30元/千克时，该品种苹果的每天销售利润最大，最大利润是400元．21. （1）解：如图所示，连接AD∵AB＝AC，BD＝DC，∴AD⊥BC即∠ADB＝90°，∴AB是⊙O的直径．（2）解：DE与⊙O相切，理由如下：如图所示，连接OD，∵OB＝OA，BD＝DC，∴OD是△ABC的中位线，∴．∵DE⊥AC，∴DE⊥OD即∠ODE＝90°，∴DE与⊙O相切．（3）解：∵AB＝AC，AD⊥BC，∠BAC＝60°，∴∠BAD＝∠DAE＝30°．∵DE⊥AC，AD⊥BD，∴AD＝2DE＝6，AB＝2BD．在△ABD中，，∴，解得．∴，∴⊙O的半径为．22. 解：（1）思路梳理
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，如图1，
∵∠ADC=∠B=90°，
∴∠FDG=180°，点F、D、G共线，
则∠DAG=∠BAE，AE=AG，BE=DG，
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°-45°=45°=∠EAF，
即∠EAF=∠FAG，
在△EAF和△GAF中，，∴△AFG≌△AEF（SAS）．∴EF=FG=DG+DF=BE+DF；
故答案为：SAS；△AFG；（2）类比引申
∠B+∠ADC=180°时，EF=BE+DF；理由如下：
∵AB=AD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，如图2所示：
∴∠BAE=∠DAG，BE=DG，
∵∠BAD=90°，∠EAF=45°，
∴∠BAE+∠DAF=45°，
∴∠EAF=∠FAG，
∵∠ADC+∠B=180°，
∴∠FDG=180°，点F、D、G共线，
在△AFE和△AFG中， ∴△AFE≌△AFG（SAS），
∴EF=FG，
∵FG=DG+DF，
∴EF=BE+DF，
故答案为：∠B+∠ADC=180°；
（3）联想拓展
猜想：DE2=BD2+EC2．理由如下：
把△ACE绕点A逆时针旋转90°到ABF的位置，连接DF，如图3所示：
则△ABF≌△ACE，∠FAE=90°，
∴∠FAB=∠CAE．BF=CE，∠ABF=∠C，
∴∠FAE=∠BAC=90°，
∵∠DAE=45°，
∴∠FAD=90°-45°=45°，
∴∠FAD=∠DAE=45°，
在△ADF和△ADE中，∴△ADF≌△ADE（SAS），
∴DF=DE，
∵∠BAC=90°，AB=AC，
∴∠ABC=∠C=45°，
∴∠C=∠ABF=45°，
∴∠DBF=∠ABF+∠ABC=90°，
∴△BDF是直角三角形，
∴BD2+BF2=DF2，
∴BD2+EC2=DE2．23. 解：因为抛物线与x轴只有一个公共点，以方程有两个相等的实数根，所以，即．（1）因为抛物线过点，所以，所以，即．所以，当时，取到最小值．（2）①因为抛物线与x轴只有一个公共点，所以抛物线上的点只能落在x轴的同侧．又点中恰有两点在抛物线的图象上，所以只能是在抛物线的图象上，由对称性可得抛物线的对称轴为，所以，即，因为，所以．又点在抛物线的图象上，所以，故抛物线的解析式为．②由题意设，则．记直线为m，分别过M，N作，垂足分别为E，F，即，因为，所以．又，所以，所以．所以，所以，即．所以，即．①把代入，得，解得，所以．②将②代入①，得，即，解得，即．所以过点A且与x轴垂直的直线为，将代入，得，即，将代入，得，即，所以，因此，所以与的面积相等．