江西省上饶市余干县四校2022-2023学年八年级下学期期中考试数学试卷(含答案)

;

八年级下学期期中考试数学练习

练习内容：（第十六章至第十八章）

一、选择题（共6小题，每小题3分，共18分）

1．下列四组数据中，不能作为直角三角形三边长的是（    ）

A．5，12，13 B．2，3，4 C．1，， D．1，2，

2．下列二次根式中，属于最简二次根式的是（    ）

A． B． C． D．

3．如图，四边形中，对角线相交于点，下列条件不能判定这个四边形是平行四边形的是（　　）

A．， B．，

C．， D．，

4．化简得(    )

A． B． C． D．

5．如图所示，中，，长度为单位1，数轴上点A所表示的数为a，则a的值是（　　）

A． B． C． D．

6．如图，在正方形中，点E、点F分别在上，且，若四边形的面积是，的长为1，则正方形的边长为（　　）

A． B． C． D．

二、填空题（共6小题，每小题3分，共18分）

7．若在实数范围内有意义，则实数的取值范围是         ．

8．若最简二次根式与是同类二次根式，则a的值是          

9．我国古代有这样一道数学问题：“枯木一根直立地上，高三丈，周八尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为3丈，底面周长为8尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是           丈．

10．直角三角形的两边a、b满足 第三边长是      ．

11．如图，在菱形中，对角线，交于点O，E为边的中点，，，则菱形的面积为     ．

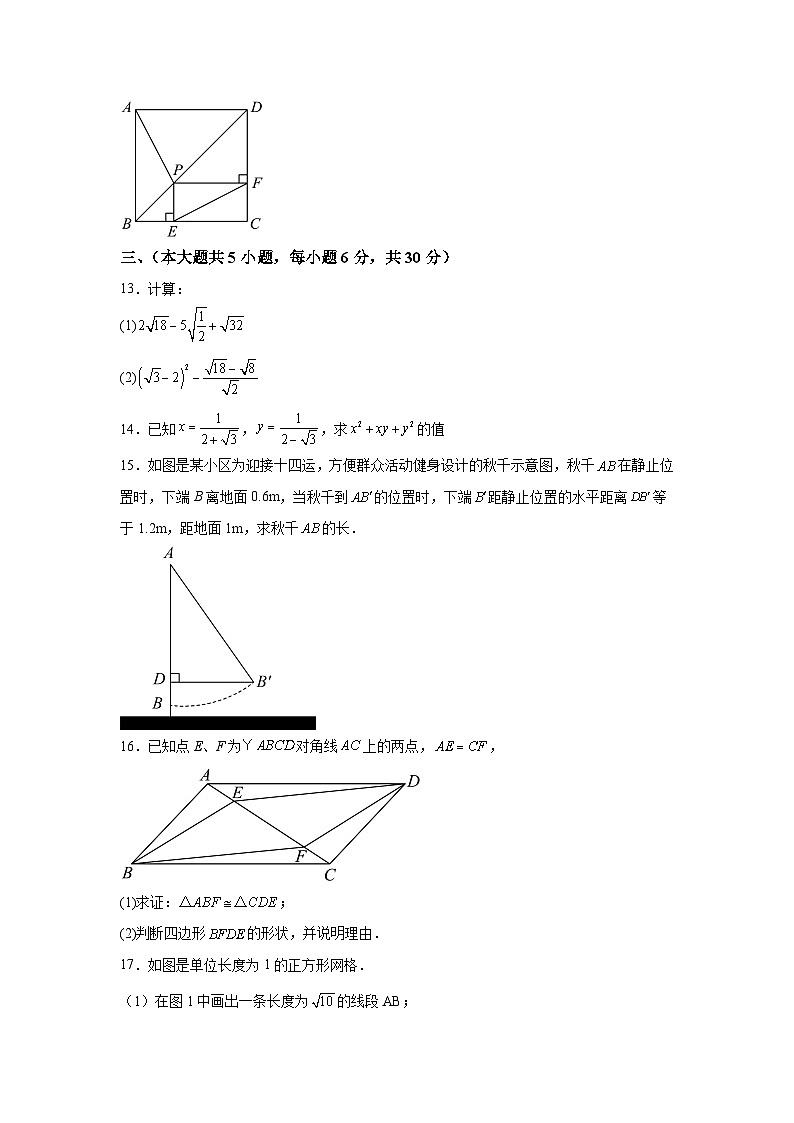
12．如图，已知正方形的边长为4，是对角线上一点，于点，于点，连接，．给出下列结论：①；②四边形的周长为8；③的最小值为2；④．其中正确结论的序号为      ．

三、（本大题共5小题，每小题6分，共30分）

13．计算：

(1)

(2)

14．已知，，求的值

15．如图是某小区为迎接十四运，方便群众活动健身设计的秋千示意图，秋千在静止位置时，下端B离地面0.6m，当秋千到的位置时，下端距静止位置的水平距离等于1.2m，距地面1m，求秋千的长．

16．已知点E、F为对角线上的两点，，

(1)求证：；

(2)判断四边形的形状，并说明理由．

17．如图是单位长度为1的正方形网格．

（1）在图1中画出一条长度为的线段AB；

（2）在图2中画出一个以格点为顶点，面积为5的正方形．

四、（本大题共3小题，每小题8分，共24分）

18．如图，中，是上的一点，若，，，．

(1)求线段的长；

(2)求的面积．

19．当时，求的值．如图是小亮和小芳的解答过程：

(1) 的解法是错误的；

(2)错误的原因在于未能正确地运用二次根式的性质： ；

(3)当时，求的值．

20．如图，矩形中，垂直平分对角线，垂足为O，点E和 F分别在边，上，连接，．

(1)求证：四边形是菱形；

(2)若，求的度数．

五、（本大题共2小题，每小题9分，共18分）

21．先观察下列等式，再回答下列问题：

①；

②；

③．

(1)请你根据上面三个等式提供的信息，猜想的结果，并验证；

(2)请你按照上面各等式反映的规律，试写出一个用n（n为正整数）表示的等式；

(3)请利用上述规律来计算（仿照上式写出过程）．

22．如图，已知在中，，，，是上的一点，，点从点出发沿射线方向以每秒个单位的速度向右运动．设点的运动时间为t，连接．

(1)当秒时，求的长度；

(2)当为等腰三角形时，求所有符合条件的值；

(3)过点作于点E，在点的运动过程中，直接写出当为何值时，能使？

六、（本大题共12分）

23．已知：在中，，点D为直线上一动点（点D不与B、C重合），以为边作正方形，连接．

(1)如图1，当点D在线段的延长线上时，请你判断线段与的数量关系，并说明理由．

(2)如图1，若，请连接并求出的长．

(3)如图2，当点D在线段的反向延长线上时，且点A、F分别在直线的两侧，其它条件不变；若连接正方形对角线，交点为O，连接，探究的形状，并说明理由．

答案

1．B

解析：解：A、，则此项能作为直角三角形三边长，不符合题意；

B、，则此项不能作为直角三角形三边长，符合题意；

C、，则此项能作为直角三角形三边长，不符合题意；

D、，则此项能作为直角三角形三边长，不符合题意；

故选：B．

2．C

解析：、，被开方数含分母，不是最简二次根式，本选项不符合题意；

、，被开方数含分母，不是最简二次根式，本选项不符合题意；

、是最简二次根式，本选项符合题意；

、，被开方数含能开得尽方的因数，不是最简二次根式，本选项不符合题意；

故选：．

3．D

解析：解：A、根据两组对边分别平行可判定四边形是平行四边形，故A选项不符合题意；

B、根据两组对边分别相等可判定四边形是平行四边形，故B选项不符合题意；

C、根据对角线相互平分可判定四边形是平行四边形，故C选项不符合题意；

D、一组对边相等、另一组对边平行不能判定四边形是平行四边形，故D选项符合题意；

故选：D．

4．A

解析：解：

，

故选：A．

5．A

解析：解：根据题意得：，

∴，

∴，

∴数轴上点A所表示的数为．

故选：A

6．D

解析：解：∵四边形是正方形，

∴，

在与中，

，

∴，

∴，

∴，

∴，

∵，

∴，

∴，

即，

∵，，

∴，

∴，

故选：D．

7．

解析：解：根据题意得：，

解得：．

故答案为：

8．5

解析：∵最简二次根式与是同类二次根式，

∴，

解得：．

故答案为：5．

9．5

解析：如图所示：表示葛藤的最短长度，

由题意可知：

（丈），（丈），

在Rt中，

（丈）．

故答案为：5.

10．或5

解析：因为直角三角形的两边a、b满足

所以

解得（舍去），（舍去），

当第三边是直角边时，长为；

当第三边是斜边时，长为；

故答案为：或5．

11．96

解析：∵菱形的对角线、交于点O，，

∴，，，

∵E为边的中点，，

∴，

∴，

∴，

∴．

故答案为： 96．

12．①②④

解析：解：∵四边形是正方形

∴

∵

∴ 是等腰直角三角形

∵

∴

故①正确

∵ 是等腰直角三角形

∴

同理

四边形的周长=

故②正确

连接，

∵ ,当 时的值最小，

∴的最小值为

故③错误

如图：过点P作 ，点G为垂足，则，延长 交 于点H

∵

∴

∴

∵

∴

∵

∴

∴

∴

故④正确，

故答案为：①②④．

13．(1)

(2)

解析：（1）解：

（2）解：

14．

解析：∵

；

把，代入，

∴

．

15．秋千的长为2m

解析：解：设，则，

由题意，得，

则，

在中，，

即，

解得：．

答：秋千的长为2m．

16．(1)见解析

(2)四边形是平行四边形，理由见解析

解析：（1）证明：

又是平行四边形

∵

 ．

（2）是平行四边形

∵

又

四边形是平行四边形.．

17．（1）见解析；（2）见解析.

解析：（1）如图1所示；

（2）如图2所示.

18．(1)

(2)84

解析：（1）∵，

∴是直角三角形，

∴，

∴是直角三角形．

∴．

（2），

∴的面积为84．

19．(1)小亮

(2)

(3)-2

解析：（1）原式，

，

∵，

∴，

∴原式，

故小亮的解法错误，

故答案为：小亮．

（2），

故答案为：．

（3）∵，

，，

∴原式，

．

20．(1)见解析

(2)

解析：（1）证明：∵垂直平分对角线，

∴，，

∵四边形是矩形，

∴，

∴，

在和中，

，

∴，

∴，

∵垂直平分对角线，

∴，，

∴，

∴四边形是菱形；

（2）解：∵四边形是矩形，

∴，，

∵，

∴，

在和中，

，

∴，

∴，

∵，

∴，

∵，

∴，

∴，

∴．

21．(1)，理由见解析

(2)

(3)

解析：（1）∵①，

②，

③，

∴，

理由：；

（2）由（1）可知，；

（3）

22．(1)

(2)或或

(3)或

解析：（1）根据题意，得，

，

在中，，

根据勾股定理，得，

答：的长为．

（2）在中，，，

根据勾股定理，得，

为等腰三角形，

若，则，

在中，根据勾股定理得，，解得．

若，则，

若，则，，

即满足条件的的值为或或．

（3）①点在线段上时，过点作于，如图所示：

则，

，

，

，

又，

≌，

，，

，

，

，

在中，由勾股定理得：，

解得：；

②点在线段的延长线上时，过点作于，如图所示

同①得：≌，

，，

，

，

，

在中，由勾股定理得：，

解得：；

综上所述，在点的运动过程中，当的值为或时，．

23．(1)，理由见解析

(2)；

(3)是等腰三角形，理由见解析

解析：（1）解：，理由如下，

∵，

∴，

∵四边形是正方形，

∴，

∵，，

∴，

在和中，，

∴，

∴；

（2）解：由（1）得，

∴，，

∴，

∵，则，

∴，

∵，

∴，

∴；

（3）解：是等腰三角形，理由如下，

∵，

∴，

则，

∵四边形是正方形，

∴，，

∵，，

∴，

在和中，，

∴，

∴，

∴，

则为直角三角形，

∵正方形中，O为中点，

∴，

∵在正方形中，，，

∴，

∴是等腰三角形．