四川省绵阳市涪城区2023届九年级上学期期中教学质量监测数学试卷(含答案)

这是一份四川省绵阳市涪城区2023届九年级上学期期中教学质量监测数学试卷(含答案)，共15页。试卷主要包含了下列结论正确的是等内容，欢迎下载使用。
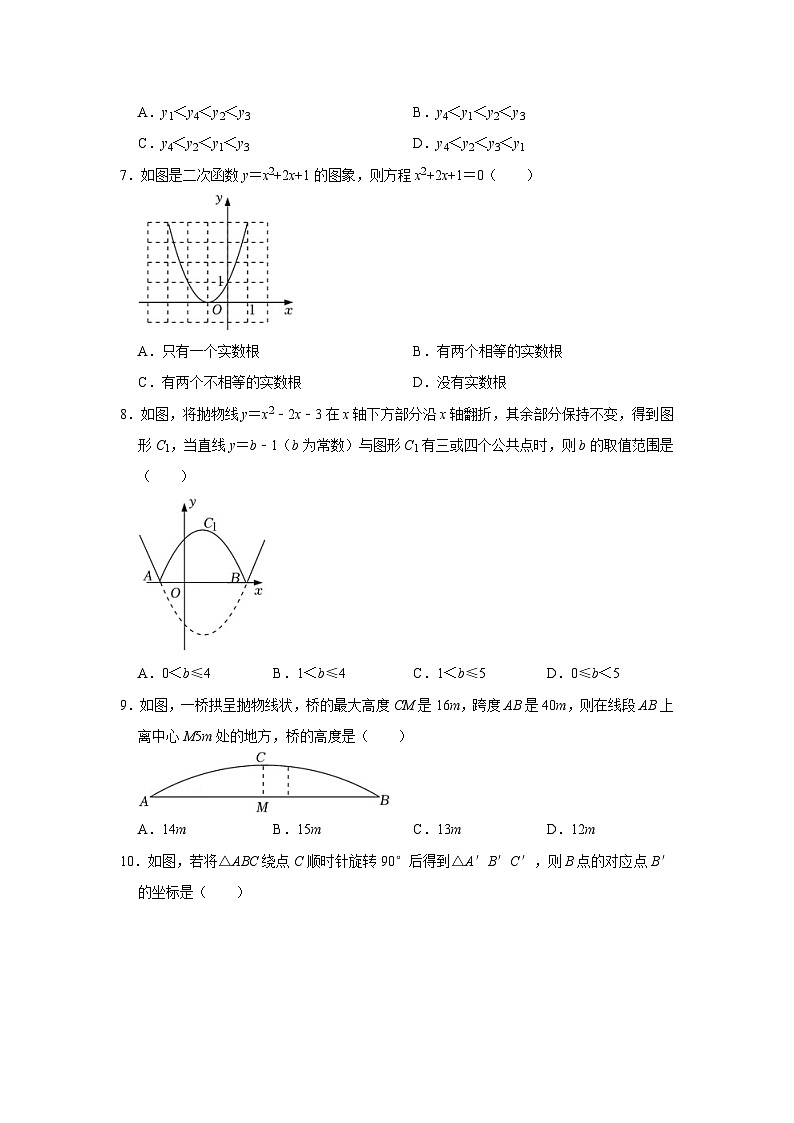
2022-2023学年九年级（上）期中教学质量监测试卷数  学一．选择题（共36分）1．下列关于防范“新冠肺炎”的标志中是轴对称图形，不是中心对称图形的是（　　）A．戴口罩讲卫生 B．勤洗手勤通风 C．有症状早就医 D．少出门少聚集2．下列结论正确的是（　　）A．半径相等的两条弧是等弧 B．半圆是弧 C．半径是弦 D．弧是半圆3．若关于x的方程x2+bx+6＝0的一个根是3，则b的值是（　　）A．2 B．﹣3 C．4 D．﹣54．若某三角形两边的长分别等于方程x（x﹣9）+4（9﹣x）＝0的两个实数根，则这个三角形的第三边长可能是（　　）A．5 B．10 C．13 D．145．在一幅长60m，宽40m的景观区域的四周铺设一条观光小道，如图所示，如果要使观光小道的总面积是2816m2，设观光小道的宽为xm，那么x满足的方程是（　　）A．2x（60+2x）+2x（40+2x）＝2816 B．（60+2x）（40+2x）＝2816 C．（60+2x）（40+2x）﹣2400＝2816 D．x（60+2x）+x（40+2x）＝28166．已知二次函数y＝ax2+bx+c图象上的点A（﹣3，y1），B（﹣1，y2），C（1，y3），D（3，y4），且y4＜y2＜y3，则y1，y2，y3，y4的大小关系是（　　）A．y1＜y4＜y2＜y3 B．y4＜y1＜y2＜y3 C．y4＜y2＜y1＜y3 D．y4＜y2＜y3＜y17．如图是二次函数y＝x2+2x+1的图象，则方程x2+2x+1＝0（　　）A．只有一个实数根 B．有两个相等的实数根 C．有两个不相等的实数根 D．没有实数根8．如图，将抛物线y＝x2﹣2x﹣3在x轴下方部分沿x轴翻折，其余部分保持不变，得到图形C1，当直线y＝b﹣1（b为常数）与图形C1有三或四个公共点时，则b的取值范围是（　　）A．0＜b≤4 B．1＜b≤4 C．1＜b≤5 D．0≤b＜59．如图，一桥拱呈抛物线状，桥的最大高度CM是16m，跨度AB是40m，则在线段AB上离中心M5m处的地方，桥的高度是（　　）A．14m B．15m C．13m D．12m10．如图，若将△ABC绕点C顺时针旋转90°后得到△A′B′C′，则B点的对应点B′的坐标是（　　）A．（﹣3，﹣2） B．（2，2） C．（3，0） D．（2，1）11．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝10，AE＝1，则弦CD的长是（　　）A． B．2 C．6 D．812．如图，四边形ABCD是⊙O的内接四边形，若∠D＝85°，则∠B的度数为（　　）A．95° B．105° C．115° D．125°二．填空题（共24分）13．若a，b，c是△ABC的三边，则关于x的方程（a+b）x2﹣2cx+a+b＝0的根的情况是 　   　．14．m是方程x2+x﹣2＝0的根，则代数式2m2+2m﹣2022的值是 　   　．15．若二次函数y＝ax2+bx﹣（a+b）图象经过A（﹣1，4），B（0，﹣1），C（1，1）三个点中的其中两个点，则该二次函数的解析式为 　   　．16．在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在第 　   　象限．17．如图，在⊙O中，AB为直径，弦CD⊥AB于点H，若AH＝CD＝10，则⊙O的半径长为 　   　．18．如图，抛物线y＝x2经过平移得到抛物线y＝ax2+bx，其对称轴与两段抛物线所围成的阴影部分的面积是8，则抛物线y＝ax2+bx的顶点坐标是 　   　．三．解答题（共90分）19．（6分）用适当的方法解下列方程：（1）x2﹣2x＝0；（2）x2﹣10x+16＝0．20．（8分）在平面直角坐标系xOy中，点（1，m），（3，n）在抛物线y＝ax2+bx+1（a，b为常数，且a≠0）上，当x＝t时函数y有最小值．（1）当m＝n，a＝1时，求抛物线的解析式及t的值；（2）若a＝b时，用n的代数式表示m；（3）已知，二次函数y＝ax2+bx+1的图象和直线y＝2ax+2b都经过点（1，m），求a2+b2的取值范围．21．（8分）如图，在平面直角坐标系中，A（﹣1，4），B（﹣4，0），C（﹣1，0）．（1）△A1B1C1与△ABC关于原点O对称，画出△A1B1C1并写出点A1的坐标；（2）△A2B2C2是△ABC绕原点O顺时针旋转90°得到的，画出△A2B2C2并写出点A2的坐标．22．（10）如图，CD是⊙O的直径，点A在DC的延长线上，∠A＝20°，AE交⊙O于点B，且AB＝OC．（1）求∠AOB的度数．（2）求∠EOD的度数．23．（8分）石拱桥是我国古代人民勤劳和智慧的结晶（如图1），隋代建造的赵州桥距今约有1400年历史，是我国古代石拱桥的代表．如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为．桥的跨度（弧所对的弦长）AB＝24m，设所在圆的圆心为O，半径OC⊥AB，垂足为D．拱高（弧的中点到弦的距离）CD＝5m．连接OB．求这座石拱桥主桥拱的半径．（精确到1m）．24．（8分）如图，AB是⊙O的直径，C是BA延长线上一点，点D在⊙O上，且CD＝OA，CD的延长线交⊙O于点E．若∠BOE＝57°，试求∠C的度数．25．（10分）在△AMB中，∠AMB＝90°，AM＝6，BM＝8，将△AMB以B为旋转中心顺时针旋转90°得到△CNB，连接AC，求AC的长．26．（10分）在平面直角坐标系xOy中，抛物线y＝x2﹣2ax+b的顶点在x轴上，若P（x1，m），Q（x2，m）（x1＜x2）是此抛物线上的两点．（1）若a＝1，①当m＝b时，求x1，x2的值；②将抛物线沿y轴平移，使得它与x轴的两个交点间的距离为4，求平移后抛物线的解析式；（2）若存在实数c，使得x1≤c﹣1，且x2＞c+7成立，则m的取值范围是 　   　．27．（10分）学校准备利用操场开元旦晚会，师生坐在足球场区域，已知足球场宽度为72m（观众席不一定要占满球场宽度），其他三边利用总长为140m的移动围栏围成一个矩形的观众席，并在观众席内按行、列，摆放单人座椅，要求每个座位占地面积为1m2（如图所示），且观众席内的区域恰好都安排了座位．（1）若观众席内有x行座椅，用含x的代数式表示每行的座椅数，并求x的最小值；（2）若全校师生共2400人，那么座位够坐吗？请说明理由．28．（12分）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0），B（3，0）与y轴交于点C，当点P从点B匀速运动到点A时，点Q恰好从点C运动到点O，过点P作PF⊥AB交抛物线于点F，交直线BC于点E，连结CF．（1）求抛物线的函数表达式．（2）若点F在第一象限，求S△CBF的最大值．（3）记BP＝t，CQ＝s．①求s关于t的函数表达式．②作点Q关于直线BC的对称点Q′，当点Q′落在△CEF的一条边上时，求s的值．
 参考答案 一．选择题 1． A．2． B．3． D．4． B．5． C．6． A．7． B．8． C．9． B．10． B．11． C．12． A．二．填空题 13． 没有实数解．14． ﹣2018．15． y＝3x2﹣2x﹣1．16． 一．17． ．18． （2，﹣4）．三．解答题 19． 解：（1）x2﹣2x＝0，x（x﹣2）＝0，∴x＝0或x﹣2＝0，∴x1＝0，x2＝2；（2）x2﹣10x+16＝0，（x﹣2）（x﹣8）＝0，∴x﹣2＝0或x﹣8＝0，∴x1＝2，x2＝8．20． 解：（1）当m＝n，则点（1，m）与点（3，m）为抛物线上的对称点，∴抛物线的对称轴为直线x＝2，即t＝2，∵a＝1，∴y＝x2+bx+1，∵﹣ ＝2，解得b＝﹣4，∴抛物线解析式为y＝x2﹣4x+1；（2）当a＝b，抛物线解析式为y＝ax2+ax+1，把（1，m），（3，n）分别代入得，∴6m﹣n＝5，∴n＝6m﹣5；（3）把（1，m）分别代入y＝ax2+bx+1和y＝2ax+2b得a+b+1＝m，2a+2b＝m，∴a+b＝1，即b＝a﹣1，∴a2+b2＝a2+（1﹣a）2＝2a2﹣2a+1＝2（a﹣）2+，∴a2+b2的最小值为，∴a2+b2的取值范围为a2+b2≥．21． 解：（1）如图，△A1B1C1即为所求．点A1的坐标为（1，﹣4）．（2）如图，△A2B2C2即为所求．点A2的坐标为（4，1）．22． 解：（1）连OB，如图，∵AB＝OC，OB＝OC，∴AB＝BO，∴∠AOB＝∠1＝∠A＝20°； （2）∵∠2＝∠A+∠1，∴∠2＝2∠A，∵OB＝OE，∴∠2＝∠E，∴∠E＝2∠A，∴∠DOE＝∠A+∠E＝3∠A＝60°．23． 解：∵OC⊥AB，∴AD＝BD，设主桥拱半径为R，由题意可知AB＝24，CD＝5，∴BD＝AB＝12，OD＝OC﹣CD＝R﹣5，∵∠ODB＝90°，∴OD2+BD2＝OB2，∴（R﹣5）2+122＝R2，解得R＝16.9≈17，答：这座石拱桥主桥拱的半径约为17m．24． 解：连接OD，∵CD＝OB＝OA＝OD，∠BOE＝57°，∴∠ODE＝2∠C，∵OD＝OE，∴∠ODE＝∠EDO＝2∠C，∴∠EOB＝∠C+∠ODE＝3∠C＝57°，∴∠C＝19°．25． 解：在Rt△AMB中，AM＝6，BM＝8，根据勾股定理可得AB＝  ＝10．根据旋转的性质可知AB＝BC，∠ABC＝90°，∴AC＝＝10．26． 解：∵抛物线y＝x2﹣2ax+b的顶点在x轴上，∴   ＝0，∴b＝a2．（1）∵a＝1，∴b＝1，∴抛物线的解析式为y＝x2﹣2x+1．①∵m＝b＝1，∴x2﹣2x+1＝1，解得：x1＝0，x2＝2；②设平移后的抛物线为y＝（x﹣1）2+k．∵抛物线的对称轴是直线x＝1，平移后与x轴的两个交点之间的距离是4，∴（3，0）是平移后的抛物线与x轴的一个交点，∴（3﹣1）2+k＝0，即k＝﹣4，∴变化过程是：将原抛物线向下平移4个单位；（2）∵x2﹣2ax+a2＝m，解得：x1＝a﹣，x2＝a+ ，∴PQ＝2．又∵x1≤c﹣1，x2≥c+7，∴2≥（c+7）﹣（c﹣1），即2＝8，∴m≥16．故答案为：m≥16．27． 解：（1）∵移动围栏的总长为140m，且观众席内有x行座椅，∴每行的座椅数为（140﹣2x）个．∵140﹣2x≤72，∴x≥34，∴x的最小值为34．（2）座位够坐，理由如下：依题意得：x（140﹣2x）＝2400，整理得：x2﹣70x+1200＝0，解得：x1＝30（不符合题意，舍去），x2＝40，∴若全校师生共2400人，那么座位够坐．28．解：（1）将点A（﹣1，0），B（3，0）代入y＝﹣x2+bx+c，得解得∴y＝﹣x2+2x+3；（2）令x＝0，则y＝3，∴C（0，3），设直线BC的解析式为y＝kx+m，∴∴∴直线BC的解析式为y＝﹣x+3，设F（t，﹣t2+2t+3），则E（t，﹣t+3），∴EF＝﹣t2+2t+3+t﹣3＝﹣t2+3t＝﹣（t﹣ ）2+，当t＝时，EF有最大值，∵S△CBF＝EF•OB＝EF，∴S△CBF的最大值为×＝；（3）①∵AB＝4，OC＝3，∴  =∵P点与Q点运动时间相同，∴= ∴s＝t；②∵BP＝t，∴P（3﹣t，0），∵OB＝OC，∴∠OCB＝45°，∵点Q关于直线BC的对称点Q′，∴∠QCQ'＝90°，当Q'落在CF上时，CF⊥y轴，∴F（2，3），∴3﹣t＝2，∴t＝1，∴s＝；当Q'落在EF上时，CQ＝CQ'＝s，∴s＝3﹣t，∴3﹣t＝t，∴t＝，∴s＝；综上所述：s的值为或．