北师大版七年级数学下册专题四模型拓展——平行线中的拐点教学课件

这是一份北师大版七年级数学下册专题四模型拓展——平行线中的拐点教学课件，共12页。
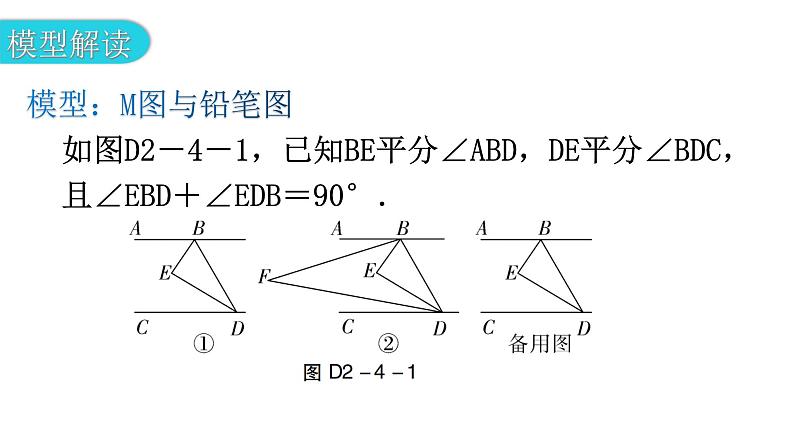
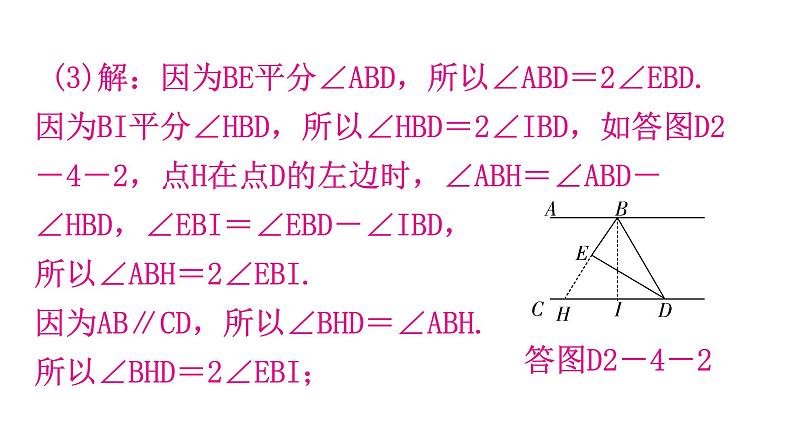
专题四 模型拓展——平行线中的拐点如图D2－4－1，已知BE平分∠ABD，DE平分∠BDC，且∠EBD＋∠EDB＝90°． 模型：M图与铅笔图(1)求证：AB∥CD；(2)如图D2－4－1②,射线BF，DF交于点F，且∠BFD＝30°，当∠ABE＝3∠ABF时，试探究∠CDF与∠CDE的比值，并说明理由；(3)若点H是直线CD上一动点(不与点D重合)，BI平分∠HBD. 请直接写出∠EBI与∠BHD的数量关系．(1)证明：因为BE平分∠ABD，DE平分∠BDC，所以∠ABD＝2∠EBD，∠CDB＝2∠EDB.又因为∠EBD＋∠EDB＝90°，所以∠ABD＋∠CDB＝2×90°＝180°. 所以AB∥CD.阅读下面材料：小亮同学遇到这样一个问题：如图D2－4－2①，AB∥CD，E为AB，CD之间一点，连接BE，DE，得到∠BED. 求证：∠BED＝∠B＋∠D. (1)小亮写出了该问题的证明，请你帮他把证明过程补充完整．证明：过点E作EF∥AB，则有∠BEF＝________．因为AB∥CD，所以________∥________.所以∠FED＝________．所以∠BED＝∠BEF＋∠FED＝∠B＋∠D. ∠BEFCD∠D(2)请你参考小亮思考问题的方法，解决问题：如图D2－4－2②，直线a∥b，点A，B在直线a上，点C，D在直线b上，连接AD，BC，BE平分∠ABC，DE平分∠ADC，且BE，DE所在的直线交于点E．①如图D2－4－2②，当点B在点A的左侧时，若∠ABC＝60°，∠ADC＝70°，求∠BED的度数；②如图D2－4－2③，当点B在点A的右侧时，设∠ABC＝α，∠ADC＝β，请你求出∠BED的度数(用含有α，β的式子表示)．