新高考数学一轮复习知识点总结与题型精练专题07 基本初等函数（含解析）

这是一份新高考数学一轮复习知识点总结与题型精练专题07 基本初等函数（含解析），共42页。

专题07 基本初等函数
【考纲要求】
1、掌握二次函数的图象与性质，会求二次函数的最值(值域)、单调区间．
2、了解指数函数模型的实际背景，理解有理数指数幂的含义，了解实数指数幂的意义，掌握幂的运算．
3、理解指数函数的概念及其单调性，掌握指数函数图象通过的特殊点，知道指数函数是重要的函数模型．
4、理解对数的概念及其运算性质，知道用换底公式将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用．
5、理解对数函数的概念及其单调性，掌握对数函数图象通过的特殊点，知道对数函数是重要的函数模型．
一、二次函数
【考点总结】
1．二次函数
(1)二次函数解析式的三种形式
①一般式：f(x)＝ax2＋bx＋c(a≠0)．
②顶点式：f(x)＝a(x－m)2＋n(a≠0)．
③零点式：f(x)＝a(x－x1)(x－x2)(a≠0)．
(2)二次函数的图象和性质
解析式
f(x)＝ax2＋bx＋c(a>0)
f(x)＝ax2＋bx＋c(a<0)
图象


定义域
(－∞，＋∞)
(－∞，＋∞)
值域


单调性
在上单调递减；
在上单调递增
在上单调递增；
在上单调递减
对称性
函数的图象关于x＝－对称
二、幂函数
【思维导图】


【考点总结】
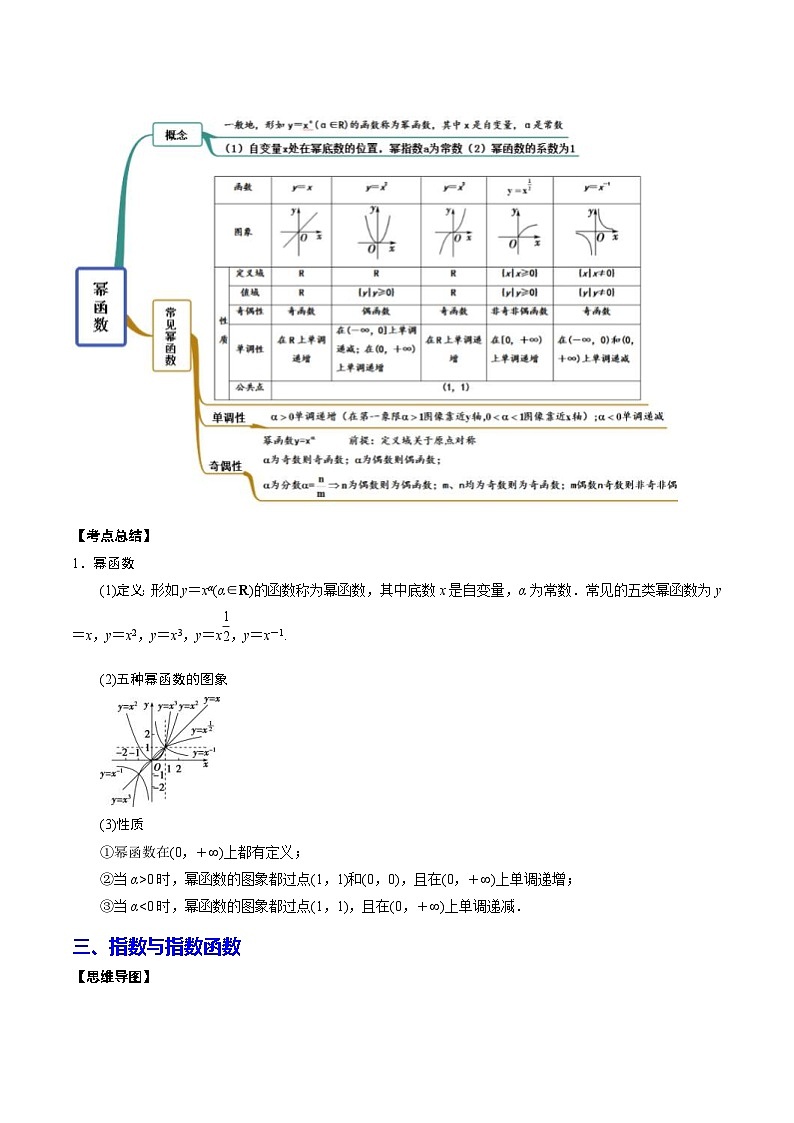
1．幂函数
(1)定义：形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．常见的五类幂函数为y＝x，y＝x2，y＝x3，y＝x，y＝x－1.
(2)五种幂函数的图象

(3)性质
①幂函数在(0，＋∞)上都有定义；
②当α>0时，幂函数的图象都过点(1，1)和(0，0)，且在(0，＋∞)上单调递增；
③当α<0时，幂函数的图象都过点(1，1)，且在(0，＋∞)上单调递减．
三、指数与指数函数
【思维导图】


【考点总结】
1．根式
(1)根式的概念
①若xn＝a，则x叫做a的n次方根，其中n>1且n∈N*.式子叫做根式，这里n叫做根指数，a叫做被开方数．
②a的n次方根的表示：
xn＝a⇒
(2)根式的性质
①()n＝a(n∈N*，且n>1)；
②＝
2．有理数指数幂
(1)幂的有关概念
①正分数指数幂：a＝(a>0，m，n∈N*，且n>1)；
②负分数指数幂：a－＝＝(a>0，m，n∈N*，且n>1)；
③0的正分数指数幂等于0，0的负分数指数幂无意义．
(2)有理数指数幂的运算性质
①aras＝ar＋s(a>0，r，s∈Q)；
②(ar)s＝ars(a>0，r，s∈Q)；
③(ab)r＝arbr(a>0，b>0，r∈Q)．
3．指数函数的图象与性质
y＝ax (a>0且a≠1)
a>1
0 图象


定义域
R
值域
(0，＋∞)
性质
过定点(0，1)
当x>0时，y>1；当x<0时，0 当x>0时，01
在R上是增函数
在R上是减函数
四、对数与对数函数


【考点总结】
1．对数
概念
如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底数N的对数，记作x＝logaN，其中a叫做对数的底数，N叫做真数，logaN叫做对数式
性质
对数式与指数式的互化：ax＝N⇔x＝logaN(a>0，且a≠1)
loga1＝0，logaa＝1，alogaN＝N(a>0，且a≠1)
运算法则
loga(M·N)＝logaM＋logaN
a>0，且a≠1，M>0，N>0
loga＝logaM－logaN
logaMn＝nlogaM(n∈R)
换底公式
logab＝(a>0，且a≠1，c>0，且c≠1，b>0)
2.对数函数的图象与性质


a>1
0 图象



续　表


a>1
0 性质
定义域：(0，＋∞)
值域：R

过定点(1，0)
当x>1时，y>0当0 当x>1时，y<0当00
在(0，＋∞)上是增函数
在(0，＋∞)上是减函数
3.反函数
指数函数y＝ax与对数函数y＝logax互为反函数，它们的图象关于直线y＝x对称．
【题型汇编】
题型一：二次函数的概念
题型二：二次函数的图象与性质
题型三：幂函数的图象与性质
题型四：指数函数的图象与性质
题型五：对数函数的图象与性质
【题型讲解】
题型一：二次函数的概念
一、单选题
1．（2022·上海松江·二模）已知正方形的边长为4，点、分别在边、上，且，，若点在正方形的边上，则的取值范围是（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
建立平面直角坐标系，利用向量的数量积运算及二次函数求值域即可得解.
【详解】
如图，建立平面直角坐标系，

则，，
当在上时，设，，
，
当时，，当时，，
即，
当在上时，设，则，
，知，
当在上时，设，，
，
当时，，当时，，
即，
当在上时，设，，
，
当时，，当时，，
即.
综上可得，，
故选：C
2．（2022·北京·北大附中三模）已知半径为的圆经过点，且与直线相切，则其圆心到直线距离的最小值为（       ）
A．1 B． C．2 D．
【答案】B
【解析】
【分析】
先求出得圆心的轨迹方程，再利用点到直线的距离公式表示出距离，最后根据二次函数的最值求解方法可求得答案.
【详解】
依题意，设圆的圆心，动点到点的距离等于到直线的距离，
根据抛物线的定义可得圆心的轨迹方程为，
设圆心到直线距离为，

当时,
故选：B
方法二：可以设与直线平行的抛物线的切线方程，联立方程，利用判别式等
于零，得到切线方程，再利用平行线的距离公式得解；
方法三：在第一象限分析问题，转化为求函数的切线与直线平行，再利用平行线的距离公式得解.
3．（2022·江西南昌·三模（理））已知的内角，，所对的边分别为，，，，，.，分别为线段，上的动点，，则的最小值为（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
根据已知条件运用正弦定理求出的长，根据设出边的关系，再利用余弦定理表示出，从函数的角度求其最值.
【详解】
依题意，如图所示，

在中，，，由正弦定理得，
，又，解得：，
设 ，则，，
，
在中，由余弦定理得，


，
对于二次函数
开口向上，对称轴
，
的最小值为.
4．（2022·北京·二模）如图，已知正方体的棱长为1，则线段上的动点P到直线的距离的最小值为（       ）


A．1 B． C． D．
【答案】D
【解析】
【分析】
利用坐标法，设，可得动点P到直线的距离为，然后利用二次函数的性质即得.
【详解】
如图建立空间直角坐标系，则，

设，则，
∴动点P到直线的距离为

，当时取等号，
即线段上的动点P到直线的距离的最小值为.
故选：D.
5．（2022·江西·上饶市第一中学二模（文））已知集合，，则（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
解不等式得集合A，求二次函数值域得集合B，然后由集合的交集运算可得.
【详解】
由解得，即，
易知，即
则.
故选：A
6．（2022·北京市第十二中学三模）若函数的值域为R，则a的取值范围是（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
由时，，由题意，当时，，对分和两种情况讨论即可求解.
【详解】
解：由时，，
因为函数的值域为R，所以当时，，
分两种情况讨论：
①当时， ，所以只需，解得，所以；
②当时，，所以只需，显然成立，所以.
综上，的取值范围是.
故选：D.
7．（2022·四川·三模（理））设函数的定义城为R，且，当时，，若存在时，使，则k的最大值为（       ）．
A．1 B．2 C． D．
【答案】D
【解析】
【分析】
先根据得到从开始，每右移1个单位，图像就会向上移1个单位，然后确定函数的由小到大，第一次取到时，的范围，进而可得该范围内函数的解析式，令，求出，进而可得k的最大值.
【详解】
当时，
由得，
即从开始，每右移1个单位，图像就会向上移1个单位，
当时，，
又，
故当函数的由小到大，第一次取到时，
又当时，，
令，解得或，
若存在时，使，则必有，
所以k的最大值为.
故选：D.
8．（2022·安徽·淮南第一中学一模（理））已知双曲线（，）的左、右焦点分别是、，且，若P是该双曲线右支上一点，且满足，则面积的最大值是（       ）
A． B．1 C． D．
【答案】A
【解析】
【分析】
根据已知条件，结合双曲线的定义求出与，然后在中，利用余弦定理求出，再根据面积公式及二次函数的知识即可求解.
【详解】
解：因为P是该双曲线右支上一点，所以由双曲线的定义有，
又，所以，，设，
所以，
所以，
所以，当且仅当时等号成立，
所以面积的最大值是，
故选：A.
9．（2022·安徽淮北·一模（理））已知是椭圆的右焦点，点在上，直线与轴交于点，点为C上的动点，则的最小值为（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
由题可得椭圆，进而可得，利用向量数量积的坐标表示可得，再结合条件及二次函数的性质即求.
【详解】
由题可得，
∴，即椭圆，
∴，直线方程为，
∴，又，
设，则，，
∴


，又，
∴当时，有最小值为.
故选：C.
10．（2022·四川巴中·一模（理））已知集合，，则（       ）
A． B．
C． D．
【答案】B
【解析】
【分析】
求出集合中的范围，与集合取交集
【详解】
集合中，根据得：，所以集合，集合，所以
故选：B
二、多选题
1．（2022·重庆·一模）已知，且，则下列结论正确的是（       ）
A．的最大值为 B．的最大值为
C．的最小值为 D．的最大值为
【答案】BC
【解析】
【分析】
利用基本不等式直接判断A；利用基本不等式求得的最大值可判断B；利用基本不等式“1”的代换可判断C；利用二次函数的性质可判断D；
【详解】
，且，，
对于A，利用基本不等式得，化简得，
当且仅当，即时，等号成立，所以的最大值为，故A错误；
对于B，，
当且仅当，即时，等号成立，所以的最大值为，故B正确；
对于C，，
当且仅当，即时，等号成立，所以的最小值为，故C正确；
对于D，
利用二次函数的性质知，当时，函数单调递减；当时，函数单调递增，
，，故D错误；
故选：BC
题型二：二次函数的图象与性质
一、单选题
1．（2022·上海浦东新·二模）已知，，，实数满足，设，，现有如下两个结论：
①对于任意的实数，存在实数，使得；
②存在实数，对于任意的，都有；
则（       ）
A．①②均正确 B．①②均不正确
C．①正确，②不正确 D．①不正确，②正确
【答案】C
【解析】
【分析】
对①，根据，的几何意义，判断得出与一定有两个交点分析即可
对②，通过化简，将题意转换为：存在实数，使得在上为减函数，再分析出当时函数有增区间，推出矛盾即可
【详解】
对①，的几何意义为与两点间的斜率，同理的几何意义为与两点间的斜率.
数形结合可得，当时，存在；当时，存在，使得，即成立.

即对于任意的实数，存在实数，使得，故①正确；
对②，若存在实数，对于任意的，都有，即，即，即.即存在实数，对于任意的，恒成立.设，则，即为减函数.故原题意可转化为：存在实数，使得在上为减函数.因为当时，，因为对称轴为，故当时一定为增函数，故不存在实数，使得在上为减函数.故②错误
故选：C
2．（2022·辽宁·三模）函数的最大值为（       ）
A．2 B．3 C．4 D．5
【答案】B
【解析】
【分析】
利用三角函数的平方关系将化为，配方后结合二次函数知识，求得答案.
【详解】
，
当时，取得最大值，且最大值为3,
故选：B
3．（2022·江西鹰潭·二模（理））已知函数的极大值点，极小值点 ，则的取值范围是 （      ）
A． B．
C． D．
【答案】B
【解析】
【分析】
求出的导函数 ，由当时取得极大值，当时取得极小值，可得、是方程的两个根，根据一元二次方程根的分布可以得到参数 、满足的不等式组，画出其表示的平面区域，根据的几何意义即可求解
【详解】

又因为当时取得极大值，当时取得极小值，可得、是方程的两个根，根据一元二次方程根的分布可得
即：作出该不等式组表示的平面区域如图中阴影部分所示（不包括边界），可求出边界交点坐标分别为 、、，表示平面区域内的点与点连线的斜率，由图可知 ，根据倾斜角的变化，可得
故选:B
4．（2022·北京昌平·二模）已知函数，则关于的不等式的解集是（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
由二次函数的性质判断区间单调性，根据解析式知恒过且，进而确定区间值域，再由对数函数性质求的对应区间值域，即可得不等式解集.
【详解】
由题设，对称轴为且图象开口向下，则在上递增，上递减，
由，即恒过且，
所以上，上，
而在上递增，且上，上，
所以的解集为.
故选：C
5．（2022·江苏·华罗庚中学三模）若函数的定义域和值域的交集为空集，则正数的取值范围是（       ）
A． B．
C． D．
【答案】B
【解析】
【分析】
首先得到函数的定义域，再分析当时的取值，即可得到，再对时分和两种情况讨论，求出此时的取值，即可得到的值域，从而得到不等式，解得即可；
【详解】
解：因为，所以的定义域为，，
当时，则在上单调递增，所以；
要使定义域和值域的交集为空集，显然，
当时，
若则，此时显然不满足定义域和值域的交集为空集，
若时在上单调递减，此时，
则，
所以，解得，即
故选：B
6．（2022·宁夏·银川一中三模（文））已知的最小值为2，则的取值范围为（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
注意观察时，，所以让时， 恒成立即可，根据参变分离和换元方法即可得解.
【详解】
当时，，
又因为的最小值为2，
，所以需要当时， 恒成立，
所以在恒成立，
所以在恒成立，
即在恒成立，
令 ，则，
原式转化为在恒成立，
是二次函数，开口向下，对称轴为直线，
所以在上 最大值为，
所以，
故选：D.
7．（2022·北京·一模）已知直线是圆的一条对称轴，则的最大值为（       ）
A． B． C．1 D．
【答案】A
【解析】
【分析】
圆心必然在直线l上，得到 的关系式，再考虑求最大值.
【详解】
由于直线l是圆的对称轴，所以圆的圆心必定在直线l上，
将圆的一般方程转变为标准方程： ，
圆心为 ，将圆心坐标代入直线l的方程得 ，
， ，
函数是开口向下，以   为对称轴的抛物线，
所以 ，
故选：A.
8．（2022·山东济南·二模）若二次函数，满足，则下列不等式成立的是（       ）
A． B．
C． D．
【答案】B
【解析】
【分析】
首先根据，判断出二次函数的对称轴，然后再根据二次函数的单调性即可得出答案.
【详解】
因为，所以二次函数的对称轴为，
又因为，所以，
又，所以.
故选：B.
二、多选题
1．（2022·福建莆田·三模）已知函数，函数，则下列结论正确的是（       ）
A．若有3个不同的零点，则a的取值范围是
B．若有4个不同的零点，则a的取值范围是
C．若有4个不同的零点，则
D．若有4个不同的零点，则的取值范围是
【答案】BCD
【解析】
【分析】
根据题意，将问题转化为函数与图像交点个数问题，进而数形结合求解即可得答案.
【详解】
解：令得，即
所以零点个数为函数与图像交点个数，
故，作出函数图像如图，

由图可知，有3个不同的零点，则a的取值范围是，故A选项错误；
有4个不同的零点，则a的取值范围是，故B选项正确；
有4个不同的零点，此时关于直线对称，所以，故C选项正确；
由C选项可知，所以，由于有4个不同的零点，a的取值范围是，故，所以，故D选项正确.
故选：BCD
题型三：幂函数的图象与性质
一、单选题
1．（2022·山东·德州市教育科学研究院三模）已知对数函数的图像经过点与点，，，，则（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
根据对数函数可以解得，，再结合中间值法比较大小．
【详解】
设，由题意可得：，则
∴
，，
∴
故选：C．
2．（2022·江西·二模（文））已知，则a，b，c的大小关系是（       ）
A． B．
C． D．
【答案】C
【解析】
【分析】
利用对数函数、三角函数、幂函数的单调性比较大小即可.
【详解】
，
因为在是单调递增函数，所以，
因为在是单调递增函数，所以
所以，
故选：C.
3．（2022·四川眉山·三模（文））下列结论正确的是（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
对于A、B：作出和在第一象限的图像判断出：在上，有，在上，有，在上，有.即可判断A、B；对于C：判断出, ，即可判断；对于D：判断出，，即可判断.
【详解】
对于A、B：
作出和在第一象限的图像如图所示：


其中的图像用虚线表示，的图像用虚线表示.
可得，在上，有，在上，有，在上，有.
因为，所以，故A正确；
因为，所以，故B错误；
对于C：,而，所以.故C错误；
对于D：，而，所以.故D错误.
故选：A
4．（2022·北京·二模）下列函数中，与函数的奇偶性相同，且在上有相同单调性的是（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
根据指对函数的性质判断A、B，由正弦函数性质判断C，对于D有，即可判断奇偶性和单调性.
【详解】
由为奇函数且在上递增，
A、B：、非奇非偶函数，排除；
C：为奇函数，但在上不单调，排除；
D：，显然且定义域关于原点对称，在上递增，满足.
故选：D
5．（2022·江西·南昌市八一中学三模（文））已知，，，则a，b，c的大小关系为（       ）
A． B．
C． D．
【答案】C
【解析】
【分析】
结合对数函数、指数函数和幂函数的单调性直接比较大小即可.
【详解】
依题意，，，而，即，故.
故选：C．
6．（2022·广东·二模）定义在上的下列函数中，既是奇函数，又是增函数的是（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
由正弦函数，指数函数和幂函数的性质对各个选项进行分析判断即可得到答案.
【详解】
A. ,由正弦函数的性质可知在上不为增函数，故排除；
B.在上单调递减，故排除；
C. ，故函数在上为偶函数，故排除；
D. ，，故函数在上为奇函数，且由幂函数的性质知在上单调递增，则在上单调递增，满足题意；
故选：D
7．（2022·内蒙古包头·二模（文））下列函数中是减函数的为（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
根据二次函数、正比例函数、指数函数、幂函数的单调性逐一判断即可.
【详解】
A：因为函数在上单调递增，所以该函数不是减函数，不符合题意；
B：因为函数是增函数，所以不符合题意；
C：因为函数是增函数，所以不符合题意；
D：因为函数是减函数，所以符合题意，
故选：D
8．（2022·安徽·芜湖一中三模（文））设，，，则a，b，c的大小关系为（       ）
A． B．
C． D．
【答案】A
【解析】
【分析】
根据指数函数和对数函数单调性，即可求解.
【详解】
解：，，，
所以，
故选：A.
二、多选题
1．（2022·山东威海·三模）若，，则（       ）
A． B．
C． D．
【答案】BC
【解析】
【分析】
根据幂函数、指数函数、对数函数的单调性分别可判断A、B、C，结合C和对数换底公式即可判断D.
【详解】
对于A，∵幂函数y=在单调递增，∴根据可知，故A错误；
对于B，∵指数函数y=在R上单调递减，∴根据可知，故B正确；
对于C，∵对数函数y=()在上单调递减，∴根据可知，故C正确；
对于D，由C可知，∴，即，故D错误．
故选：BC．
2．（2022·山东滨州·二模）若实数a，b满足，则下列结论中正确的是（       ）
A． B．
C． D．
【答案】BCD
【解析】
【分析】
根据给定条件，求出a，b的关系，再利用不等式性质判断A，B；指对数函数、幂函数单调性分析判断C，D作答.
【详解】
因，则，于是有，A不正确；
，即，B正确；
由得：，因此，，C正确；
因，函数在R上单调递减，函数在上单调递增，则，D正确.
故选：BCD
题型四：指数的图象与性质
一、单选题
1．（2022·青海·大通回族土族自治县教学研究室三模（文））已知，，，则正数，，的大小关系为（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
由已知求出m，n，p，再借助商值比较法及“媒介”数推理判断作答.
【详解】
由，得，由，得，
因此，，即，
由，得，于是得，
所以正数，，的大小关系为.
故选：A
2．（2022·青海·大通回族土族自治县教学研究室三模（文））若函数满足，且当时，，则（       ）
A． B．10 C．4 D．2
【答案】B
【解析】
【分析】
首先得到的周期，再根据函数的周期性计算可得；
【详解】
解：由，得，
∴函数是周期函数，且4是它的一个周期，
又当时，，
∴；
故选：B.
3．（2022·山东临沂·三模）已知，则a，b，c的大小关系是（       ）
A． B．
C． D．
【答案】C
【解析】
【分析】
分别化简即可明显比较出三者大小关系.
【详解】
因为，，
所以.
故选：C.
4．（2022·江苏·华罗庚中学三模）已知，则a，b，c的大小关系是（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
利用三角函数、对数、指数函数的单调性判断可得答案.
【详解】
，
，
，
所以．
故选：C．
5．（2022·江西师大附中三模（理））设．则a，b，c大小关系是（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
根据自然常数的定义和指数幂的运算性质可知、，构造函数，利用导数研究函数的单调性可得，进而可得，即可得出结果.
【详解】
由，故；
，故；
假设，有，
令，则，所以在上单调递增，
而，则，所以成立，；
故．
故选：A．
6．（2022·广西·贵港市高级中学三模（理））已知集合，，则（       ）
A． B．
C． D．
【答案】A
【解析】
【分析】
先解出集合A、B，再求．
【详解】
集合，，
所以．
故选：A．
7．（2022·天津市武清区杨村第一中学二模）设，则a，b，c的大小关系为（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
根据对数函数、指数函数的单调性以及作商法比较大小，即可求解.
【详解】
依题意，，
，
所以
故选：A
8．（2022·山西太原·三模（理））设，则（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
根据对数和指数互化即可求解.
【详解】
，则在定义域内单调递增. 故 .
故选：D
二、多选题
1．（2022·山东烟台·三模）二进制是计算中广泛采用的一种数制，由18世纪德国数理哲学家莱布尼兹发现，二进制数据是用0和1两个数码来表示的数.现采用类似于二进制数的方法构造数列：正整数，其中（），记.如，，则下列结论正确的有（       ）
A． B． C． D．
【答案】BD
【解析】
【分析】
求得否定选项A；求得并与比较判断选项B；求得并与比较判断选项C；分别求得、并进行比较判断选项D.
【详解】
选项A：，则.判断错误；
选项B：，
则，
则.判断正确；
选项C：，
则，
.判断错误；
选项D：，
则



则
，则.判断正确.
故选：BD
2．（2022·山东烟台·三模）某公司通过统计分析发现，工人工作效率与工作年限（），劳累程度（），劳动动机（）相关，并建立了数学模型.已知甲､乙为该公司的员工，则下列说法正确的有（       ）
A．甲与乙工作年限相同，且甲比乙工作效率高，劳动动机低，则甲比乙劳累程度强
B．甲与乙劳动动机相同，且甲比乙工作效率高，工作年限短，则甲比乙劳累程度弱
C．甲与乙劳累程度相同，且甲比乙工作年限长，劳动动机高，则甲比乙工作效率高
D．甲与乙劳动动机相同，且甲比乙工作年限长，劳累程度弱，则甲比乙工作效率高
【答案】BCD
【解析】
【分析】
利用指数函数的性质，幂函数的性质逐项分析即得.
【详解】
设甲与乙的工人工作效率，工作年限，劳累程度，劳动动机，
对于A，，，，，
∴，，
，
所以，即甲比乙劳累程度弱，故A错误；
对于B，，，，
∴，，
∴，
所以，即甲比乙劳累程度弱，故B正确.
对于C，，，，
∴，，
则，
∴，即甲比乙工作效率高，故C正确；
对于D，，，，，
∴，，
则，
∴，即甲比乙工作效率高，故D 正确；
故选：BCD.
题型五：对数函数的图象与性质
一、单选题
1．（2022·浙江·高考真题）已知，则（       ）
A．25 B．5 C． D．
【答案】C
【解析】
【分析】
根据指数式与对数式的互化，幂的运算性质以及对数的运算性质即可解出．
【详解】
因为，，即，所以．
故选：C.
2．（2022·北京·高考真题）在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献．如图描述了一定条件下二氧化碳所处的状态与T和的关系，其中T表示温度，单位是K；P表示压强，单位是．下列结论中正确的是（       ）


A．当，时，二氧化碳处于液态
B．当，时，二氧化碳处于气态
C．当，时，二氧化碳处于超临界状态
D．当，时，二氧化碳处于超临界状态
【答案】D
【解析】
【分析】
根据与的关系图可得正确的选项.
【详解】
当，时，，此时二氧化碳处于固态，故A错误.
当，时，，此时二氧化碳处于液态，故B错误.
当，时，与4非常接近，故此时二氧化碳处于固态，
另一方面，时对应的是非超临界状态，故C错误.
当，时，因, 故此时二氧化碳处于超临界状态，故D正确.
故选：D
3．（2022·全国·高考真题）设，则（       ）
A． B． C． D．
【答案】C
【解析】
【分析】
构造函数， 导数判断其单调性，由此确定的大小.
【详解】
设，因为，
当时，，当时，
所以函数在单调递减，在上单调递增，
所以，所以，故，即，
所以，所以，故，所以，
故，
设，则,
令，，
当时，，函数单调递减，
当时，，函数单调递增，
又，
所以当时，，
所以当时，，函数单调递增，
所以，即，所以
故选：C.
4．（2022·上海青浦·二模）“”成立的一个必要而不充分条件是（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
先求解，再根据必要不充分条件的意义对比选项判断即可
【详解】
由有，解得，故“”成立的一个必要而不充分条件是“”
故选：D
5．（2022·黑龙江·鸡西市第四中学三模（理））若两个函数的图象经过若干次平移后能够重合，则称这两个函数为“同形”函数，给出下列三个函数：，，，则（       ）
A．，，为“同形”函数
B．，为“同形”函数，且它们与不为“同形”函数
C．，为“同形”函数，且它们与不为“同形”函数
D．，为“同形”函数，且它们与不为“同形”函数
【答案】A
【解析】
【分析】
根据题中“同形”函数的定义和、均可化简成以3为底的指数形式，可得答案．
【详解】
解：，
，
故，的图象可分别由的图象向左平移个单位、向右平移1个单位得到，
故，，为“同形”函数．
故选：A．
6．（2022·北京·北大附中三模）已知函数，则不等式的解集是（       ）
A． B．
C． D．
【答案】D
【解析】
【分析】
由可得，在同一坐标系中作出两函数的图象，即可得答案.
【详解】
解：依题意，等价于，
在同一坐标系中作出，的图象，如图所示：


如图可得的解集为：.
故选：D.
7．（2022·北京·人大附中三模）已知函数，则不等式的解集是（       ）
A． B． C． D．
【答案】B
【解析】
【分析】
求出的定义域，判断出其在上为增函数，由即可得到不等式的解集.
【详解】
函数的定义域为.
因为在上为增函数，在上为增函数，
所以在上为增函数.
又，
所以不等式的解集为.
故选：B
8．（2022·江西师大附中三模（理））已知集合，则（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
根据分式不等式和对数不等式的运算求出集合A、B，结合并集的定义和运算即可得出结果.
【详解】
由题意得，
由，
即，
，即，
所以.
故选：D.
二、多选题
1．（2022·广东佛山·三模）已知，则下列不等式成立的是（       ）
A． B． C． D．
【答案】BC
【解析】
【分析】
作差法判断选项A；利用对数函数单调性判断选项B；利用幂函数指数函数对数函数的单调性去判断选项C；举反例排除选项D.
【详解】
选项A：
由，可得，
则，，
则，则.判断错误；
选项B：由，可得为上减函数，
又，则.判断正确；
选项C：由，可知为R上减函数，又，则
由，可知为上增函数，又，则，则
又为上增函数，则，则.判断正确；
选项D：令，则，
，
则，即.判断错误.
故选：BC
2．（2022·湖北·荆门市龙泉中学二模）已知函数，且正实数，满足，则下列结论可能成立的是（       ）
A． B．的最大值为
C． D．的最小值为
【答案】AC
【解析】
【分析】
去绝对值分类讨论，判断一个命题是假命题要举反例
【详解】
当，时，，
则
所以，所以，故A正确
当，时，，，
则
所以，故C正确
当，时，，
则
所以
对于B，当，，且时
取，时，
（，）
当，且时
取，时，
当，且时，
取，时，
故B错误
对于D， 当，且时，，时，等号成立，故D错误
故选：AC