新高考数学一轮复习知识点总结与题型精练专题21 空间向量与立体几何（含解析）

这是一份新高考数学一轮复习知识点总结与题型精练专题21 空间向量与立体几何（含解析），共33页。
专题21 空间向量与立体几何
【考纲要求】
1、理解空间向量的概念、运算、基本定理，理解直线的方向向量与平面的法向量的意义；
2、会用待定系数法求平面的法向量，能用向量语言表述线线、线面、面面的垂直和平行关系；
3、体会向量方法在研究几何问题中的作用，掌握利用向量法法求空间角的方法。
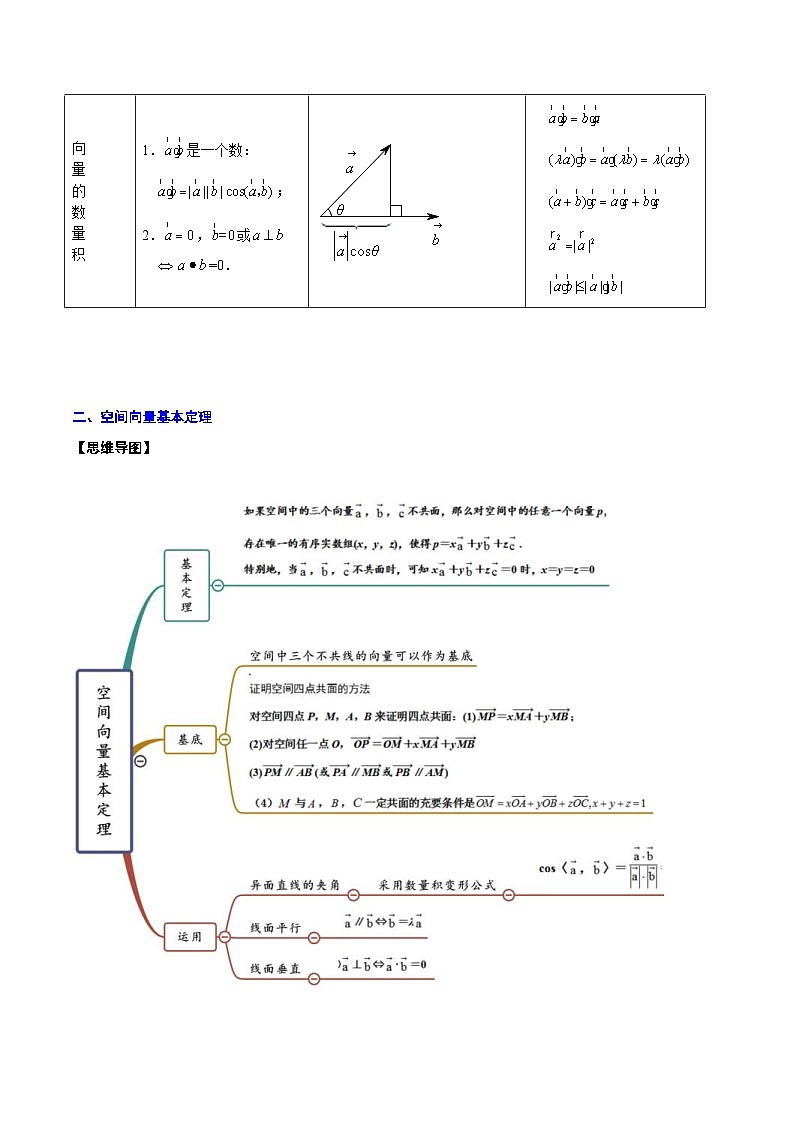
一、空间向量及其运算
【思维导图】


1、空间向量的有关概念
空间向量：空间中，既有大小又有方向的量；
空间向量的表示：一种是用有向线段表示，叫作起点，叫作终点；
一种是用小写字母（印刷体）表示，也可以用（而手写体）表示．
向量的长度（模）：表示空间向量的有向线段的长度叫做向量的长度或模，记作或．
向量的夹角：过空间任意一点作向量的相等向量和，则叫作向量的夹角，记作，规定．如图：

零向量：长度为0或者说起点和终点重合的向量，记为0．规定：0与任意向量平行．
单位向量：长度为1的空间向量，即．
相等向量：方向相同且模相等的向量．
相反向量：方向相反但模相等的向量．
共线向量（平行向量）：如果表示空间向量的有向线段所在的直线互相平行或重合．
平行于记作，此时．=0或=p．
共面向量：平行于同一个平面的向量，叫做共面向量．
要点诠释：
（1）数学中讨论的向量是自由向量，即与向量的起点无关，只与大小和方向有关． 只要不改变大小和方向，空间向量可在空间内任意平移；
（2）当我们说向量、共线（或//）时，表示、的有向线段所在的直线可能是同一直线，也可能是平行直线．
（3）对于任意一个非零向量，我们把叫作向量的单位向量，记作．与同向．
（4）当=0或p时，向量平行于，记作；当 =时，向量垂直，记作．
2、空间向量的基本运算
空间向量的基本运算：
运算类型
几何方法

运算性质
向
量
的
加
法
1平行四边形法则：


加法交换率：

加法结合率：





2三角形法则：


向
量
的
减
法
三角形法则：



向
量
的
乘
法
是一个向量，满足：
>0时，与同向；