新高考数学一轮复习知识点总结与题型精练专题25 计数原理（含解析）

这是一份新高考数学一轮复习知识点总结与题型精练专题25 计数原理（含解析），共31页。

专题25 计数原理
【考纲要求】
1、 理解分类计数原理与分步计数原理，培养学生的分析概括能力。
2、 理解排列组合的意义，会用排列数和组合数的公式
3、 理解二项式的性质，掌握多项式展开式的特殊项和系数问题
一、两种计数原理
【思维导图】

【考点总结】
1．分类加法计数原理
完成一件事有两类不同方案，在第1类方案中有m种不同的方法，在第2类方案中有n种不同的方法，
那么完成这件事共有N＝m＋n种不同的方法．
2．分步乘法计数原理
完成一件事需要两个步骤，做第1步有m种不同的方法，做第2步有n种不同的方法，
那么完成这件事共有N＝m×n种不同的方法．
3．分类加法计数原理和分步乘法计数原理的区别
原理
分类加法计数原理
分步乘法计数原理
联系
两个计数原理都是对完成一件事的方法种数而言
区别一
每类办法都能独立完成这件事，它是独立的、一次的，且每次得到的是最后结果，只需一种方法就可完成这件事
每一步得到的只是中间结果，任何一步都不能独立完成这件事，缺少任何一步也不可，只有各步骤都完成了才能完成这件事
区别二
各类办法之间是互斥的、并列的、独立的
各步之间是相互依存的，并且既不能重复也不能遗漏
二、排列与组合
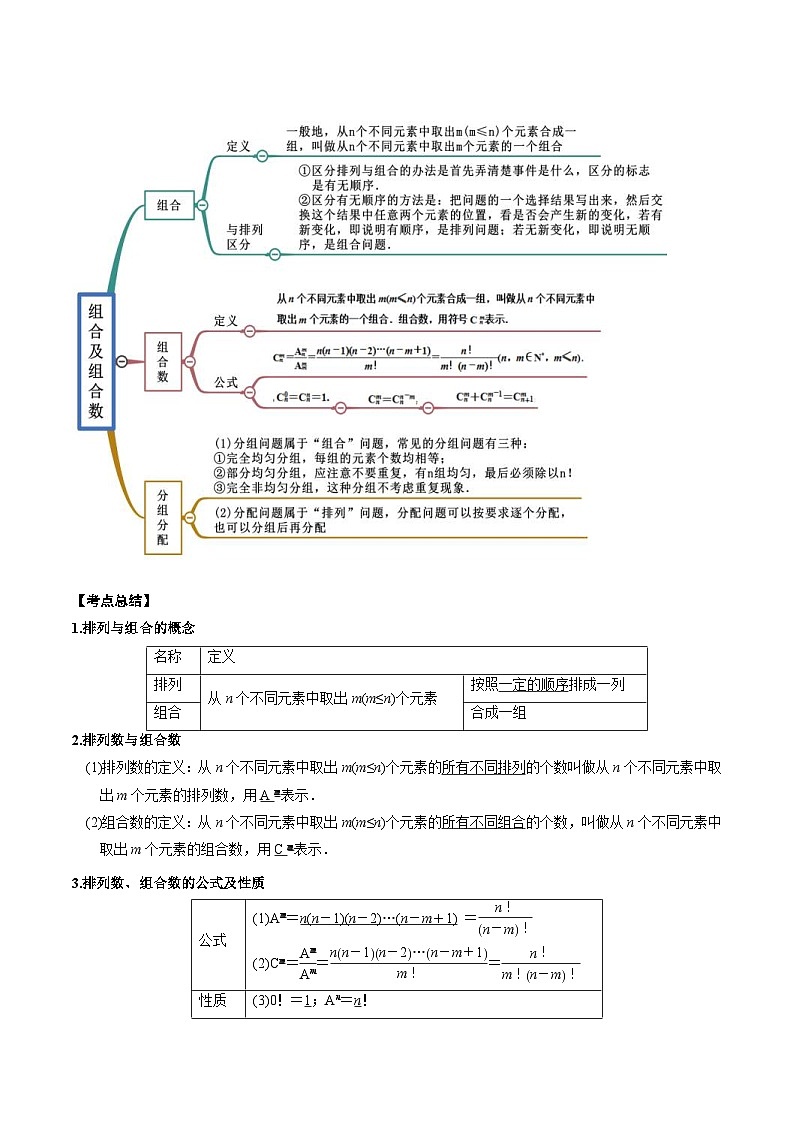
【思维导图】


【考点总结】
1.排列与组合的概念
名称
定义
排列
从n个不同元素中取出m(m≤n)个元素
按照一定的顺序排成一列
组合
合成一组
2.排列数与组合数
(1)排列数的定义：从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数叫做从n个不同元素中取出m个元素的排列数，用A表示．
(2)组合数的定义：从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数，叫做从n个不同元素中取出m个元素的组合数，用C表示．
3.排列数、组合数的公式及性质
公式
(1)A＝n(n－1)(n－2)…(n－m＋1) ＝
(2)C＝＝＝
性质
(3)0！＝1；A＝n！
(4)C＝C；C＝C＋C
三、二项式定理
【思维导图】

【考点总结】
1. 二项式定理
，这个公式所表示的定理叫做二项式定理，右边的多项式叫做的二项展开式，其中的系数 ()叫做二项式系数．式中的叫做二项展开式的通项，用表示，即展开式的第项；.
2．二项展开式形式上的特点
(1)项数为.
(2)各项的次数都等于二项式的幂指数，即与的指数的和为.
(3)字母按降幂排列，从第一项开始，次数由逐项减1直到零；字母按升幂排列，从第一项起，次数由零逐项增1直到.
(4)二项式的系数从，，一直到，.
3. 二项式系数的性质
(1)对称性：与首末两端“等距离”的两个二项式系数相等，即，，，.
(2)增减性与最大值：二项式系数，当时，二项式系数是递增的；由对称性知：当时，二项式系数是递减的．
当是偶数时，中间的一项取得最大值．
当是奇数时，中间两项 和相等，且同时取得最大值．
(3)各二项式系数的和
的展开式的各个二项式系数的和等于，即，二项展开式中，偶数项的二项式系数的和等于奇数项的二项式系数的和，即，
4.二项式定理的应用
（1）求某些多项式系数的和；
（2）证明一些简单的组合恒等式；
（3）证明整除性,①求数的末位；②数的整除性及求系数；③简单多项式的整除问题；
（4）近似计算.当充分小时，我们常用下列公式估计近似值：
①；②；
（5）证明不等式.
【题型汇编】
题型一：两种计数原理
题型二：排列与组合
题型三：二项式定理
【题型讲解】
题型一：两种计数原理
一、单选题
1．（2022·浙江·杭州四中高二期中）甲、乙、丙三人参加四项比赛，所有比赛均无并列名次，则不同的夺冠情况共有（    ）种.
A． B． C． D．
【答案】C
【分析】每个冠军都有3种可能，因为有四项比赛，根据乘法原理，可得冠军获奖者的可能情况．
【详解】解：由题意，每项比赛的冠军都有3种可能，
因为有四项比赛，所以冠军获奖者共有种可能
故选：C．
2．（2022·福建·厦门海沧实验中学高二期中）元旦来临之际，某寝室四人各写一张贺卡，先集中起来，然后每人从中拿一张别人送出的贺卡，则四张贺卡不同的分配方式有（    ）
A．6种 B．9种 C．11种 D．23种
【答案】B
【分析】由题可得当A拿贺卡b时有三种不同的分配方式，利用分类加法计数原理即得；或利用分步乘法计数原理，A先拿，有3种，此时被A拿走的那张贺卡的人也有3种不同的取法，进而即得.
【详解】解法1：设四人A、B、C、D写的贺卡分别是a、b、c、d，
当A拿贺卡b，则B可拿a、c、d中的任何一张，即B拿a，C拿d，D拿c，或B拿c，D拿a，C拿d，或B拿d，C拿a，D拿c，
所以A拿b时有三种不同的分配方式；
同理，A拿c，d时也各有三种不同的分配方式，
由分类加法计数原理，四张贺卡共有（种）分配方式；
解法2：让四人A、B、C、D依次拿一张别人送出的贺卡，
如果A先拿，有3种，此时被A拿走的那张贺卡的人也有3种不同的取法，
接下来，剩下的两个人都各只有1种取法，
由分步乘法计数原理，四张贺卡不同的分配方式有（种）．
故选：B.
3．（2023·全国·高三专题练习）四色定理又称四色猜想，是世界近代三大数学难题之一．它是于1852年由毕业于伦敦大学的格斯里提出来的，其内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色”．某校数学兴趣小组在研究给四棱锥的各个面涂颜色时，提出如下的“四色问题”：要求相邻面（含公共棱的面）不得使用同一颜色，现有4种颜色可供选择，则不同的涂法有（    ）
A．36种 B．72种 C．48种 D．24种
【答案】B
【分析】利用分步乘法原理和分类加法原理分析求解
【详解】依次涂色，底面ABCD的涂色有4种选择，侧面PAB的涂色有3种选择，侧面PBC的涂色有2种选择．
①若侧面PCD与侧面PAB所涂颜色相同，则侧面PAD的涂色有2种选择；
②若侧面PCD与侧面PAB所涂颜色不同，则侧面PCD的涂色有1种选择，侧面PAD的涂色有1种选择．
综上，不同的涂法种数为．
故选：B．

4．（2022·全国·高三专题练习）在一次运动会上有四项比赛的冠军在甲、乙、丙三人中产生，那么不同的夺冠情况共有（    ）种
A． B． C． D．
【答案】C
【分析】利用分步乘法原理求解.
【详解】由题意四项比赛的冠军依次在甲、乙、丙三人中选取，每项冠军都有3种选取方法，由乘法原理共有种．故A，B，D错误.
故选：C．
5．（2022·全国·高三专题练习）将6封信投入4个邮筒，且6封信全部投完，不同的投法有（    ）
A．种 B．种 C．4种 D．24科
【答案】A
【分析】根据乘法原理求解即可
【详解】将6封信投入4个邮筒，且6封信全部投完，根据乘法原理共有种
故选：A
6．（2022·全国·高三专题练习）从数字1，2，3，4中取出3个数字（允许重复），组成三位数，各位数字之和等于6，则这样的三位数的个数为（    ）
A．7 B．9 C．10 D．13
【答案】C
【分析】根据各位数字之和等于6的所有可能情况，①1，1，4，②1，2，3，③2，2，2三种情况分别讨论求和即可
【详解】其中各位数字之和等于6的三位数可分为以下情形：
①由1，1，4三个数字组成的三位数：114，141，411共3个；
②由1，2，3三个数字组成的三位数：123，132，213，231，312，321共6个；
③由2，2，2三个数字可以组成1个三位数，即222．
共有个，
故选：C．

二、多选题
7．（2022·广东·雷州市白沙中学高二阶段练习）已知数字，由它们组成四位数，下列说法正确的有（    ）
A．组成可以有重复数字的四位数有个
B．组成无重复数字的四位数有96个
C．组成无重复数字的四位偶数有66个
D．组成无重复数字的四位奇数有28个
【答案】AB
【分析】根据题意，由分类分步计数原理依次分析各选项，即可得答案.
【详解】解：对A：四位数的首位不能为0，有4种情况，其他数位有5种情况，则组成可以有重复数字的四位数有个，故选项A正确；
对B：四位数的首位不能为0，有4种情况，在剩下的4个数字中任选3个，排在后面3 个数位，有种情况，则组成无重复数字的四位数有个，故选项B正确；
对C：若0在个位，有个四位偶数，若0不在个位，有个四位偶数，则组成无重复数字的四位偶数共有个四位偶数，故选项C错误；
对D：组成无重复数字的四位奇数有个，故选项D错误；
故选：AB.
8．（2022·湖南·周南中学高二期末）现有不同的红球4个，黄球5个，绿球6个，则下列说法正确的是（       ）
A．从中选出2个球，正好一红一黄，有9种不同的选法
B．若每种颜色选出1个球，有120种不同的选法
C．若要选出不同颜色的2个球，有31种不同的选法
D．若要不放回地依次选出2个球，有210种不同的选法
【答案】BD
【分析】根据分步与分类计数原理逐个求解即可
【详解】对A，从中选出2个球，正好一红一黄，有种不同的选法，所以该选项错误：
对B，若每种颜色选出1个球，有种不同的选法，所以该选项正确；
对C，若要选出不同颜色的2个球，有种不同的选法，所以该选项错误；
对D，若要不放回地依次选出2个球，有种不同的选法，所以该选项正确.
故选：BD
9．（2022·广东·顺德一中高二期中）现有3名老师，8名男生和5名女生共16人，有一项活动需派人参加，则下列命题中正确的是（    ）
A．只需1人参加，有16种不同选法
B．若需老师、男生、女生各1人参加，则有120种不同选法
C．若需1名老师和1名学生参加，则有39种不同选法
D．若需3名老师和1名学生参加，则有56种不同选法
【答案】ABC
【分析】根据分类计数原理和分步计数原理依次讨论各选项即可求解.
【详解】解：选项A，分三类：取老师有3种选法，取男生有8种选法，取女生有5种选法，故共有种选法，故A正确；
选项B，分三步：第一步选老师，第二步选男生，第三步选女生，
故共有种选法，故B正确；
选项C，分两步：第一步选老师，第二步选学生，第二步，又分为两类：第一类选男生，第二类选女生，故共有种选法，故C正确；
选项D，若需3名老师和1名学生参加，则有13种不同选法，故D错误.
故选：ABC.

三、解答题
10．（2022·全国·高二课时练习）从1、2、3三个数中取1个数作分子，从4、5、6、7四个数中取1个数作分母，组成一个分数，这样能组成多少个值不相等的分数？写出这些分数．
【答案】11个；具体分数见解析.
【分析】由分步乘法计数原理可得组成分数的个数，其中，减去1个值相等的分数即可得值不同的分数的个数，再一一写出即可.
【详解】解：从1、2、3三个数中取1个数作分子，从4、5、6、7四个数中取1个数作分母，组成的分数个数为，
其中，所以组成值不相等的分数个数为，
它们是、、、、、、、、、、．
11．（2022·江苏·响水县第二中学高二期中）有6名同学报名参加三个智力竞赛项目，在下列情况下各有多少种不同的报名方法？（不一定6名同学都参加）
(1)每人恰好参加一项，每项人数不限；
(2)每项限报一人，但每人参加的项目不限.
【答案】(1)
(2)

【分析】（1）由人选项目，分个步骤完成，根据分步乘法计数原理可求解；
（2）由项目找人，分三个步骤完成，根据分步乘法计数原理可求解；
（1）
每人都可以从这三个智力竞赛项目中选报一项，各有3种不同的报名方法．
根据分步乘法计数原理，可得不同的报名方法种数为．
（2）
每项限报一人，但每人参加的项目不限．
因此每一个项目都可以从这6人中选出1人参加．根据分步乘法计数原理，可得不同的报名方法种数为．
12．（2023·全国·高三专题练习）相邻的个车位中停放了辆不同的车，现将所有车开出后再重新停入这个车位中．
(1)若要求有辆车不得停在原来的车位中，有多少种不同的停法？
(2)若要求所有车都不得停在原来的车位中，有多少种不同的停法？
【答案】(1)
(2)

【分析】（1）利用分步乘法计数原理直接计算即可；
（2）利用分步乘法计数原理直接计算即可.
（1）
可分成两步完成：第一步，先选出停在原来车位的那辆车，有种情况，
第二步，停放剩下的辆车，将剩余辆车分别编号为，，，将剩余个停车位分别编号为一、二、三，设车先选停车位，此时有种停法，剩余两辆车有且只有种停法，所以第二部有种停法，
根据分步乘法计数原理，共有种停法；
（2）
将辆车分别编号为，，，，将个停车位分别编号为一、二、三、四．不妨设车先选停车位，此时有种停法，若车选了二号停车位，那么车再选，有种停法，剩下的车和车都只有种停法，故共有种停法．
题型二：排列与组合
一、单选题
1．（2023·全国·高三专题练习）高中数学新教材有必修一和必修二，选择性必修有一､二､三共5本书，把这5本书放在书架上排成一排，必修一､必修二不相邻的排列方法种数是（    ）
A．72 B．144 C．48 D．36
【答案】A
【分析】先将选择性必修有一､二､三这三本书排成一排的方法种数, 先将选择性必修有一､二､三这三本书排成一排的方法种数，由分步计数原理即可得出答案.
【详解】先将选择性必修有一､二､三这三本书排成一排，有种方法，
再将必修一､必修二这两本书插入两个空隙中，有种方法，
所以把这5本书放在书架上排成一排，必修一､必修二不相邻的排列方法种数是：.
故选：A.
2．（2023·全国·高三专题练习）某密码锁的一个密码由3位数字组成，每一位均可取0，1，2，…，9这10个数字中的一个，小明随机设置了一个密码，则恰有两个位置数字相同的概率为（    ）

A．0.09 B．0.12 C．0.18 D．0.27
【答案】D
【分析】根据分布计数原理及组合数的定义，结合古典概型的计算公式即可求解.
【详解】先从3个位置中选1个，从0到9这10个数字中选一个数字放入，剩下的两个位置再从剩下的9个数字中选一个数字放入（两个位置数字相同），有种方法，所以所求概率．
故选: D.
3．（2022·四川·射洪中学高三阶段练习（理））2022年遂宁主城区突发“920疫情”，23日凌晨2时，射洪组织五支“最美逆行医疗队”去支援遂宁主城区，将分派到遂宁船山区、遂宁经开区、遂宁高新区进行核酸采样服务，每支医疗队只能去一个区，每区至少有一支医疗队，若恰有两支医疗队者被分派到高新区，则不同的安排方法共有（    ）
A．30种 B．40种 C．50种 D．60种
【答案】D
【分析】先从5支医疗队中选取2支医疗队去高新区，再将剩下的3支医疗队分配到船山区与经开区，最后根据分步乘法原理求解即可.
【详解】解：先从5支医疗队中选取2支医疗队去高新区，有种不同的选派方案，
再将剩下的3对医疗队分配到船山区与经开区，有种不同的选派方案，
所以，根据分步乘法原理，不同的安排方案有种.
故选：D
4．（2022·山东·高密三中高三阶段练习）已知n，m为正整数，且，则在下列各式中错误的是（    ）
A．； B．； C．； D．
【答案】C
【分析】据组合数的性质及排列数公式计算可得
【详解】解：对于A，，故正确；
对于B，因为，所以，故正确；
对于C，因为n，m为正整数，且，
所以令，则，，此时，故错误；
对于D，，故正确；
故选：C
5．（2022·江苏镇江·高三开学考试）已知，为正整数，且，则在下列各式中，正确的个数是（    ）
①；②；③；④
A．1 B．2 C．3 D．4
【答案】C
【分析】根据组合数的性质及排列数公式计算可得.
【详解】解：对于①，故①正确；
对于②因为，所以，故②正确；
对于③因为，故③错误；
对于④，故④正确；
故选：C
6．（2023·全国·高三专题练习）若，则（    ）
A．7 B．8 C．9 D．10
【答案】B
【分析】根据排列数的计算公式即可求解.
【详解】由题意，得，化简可得，解得．
故选:B
7．（2023·全国·高三专题练习）宋元时期是我国古代数学非常辉煌的时期，涌现了一大批卓有成就的数学家，其中秦九韶、李冶、杨辉和朱世杰成就最为突出，被誉为“宋元数学四大家”．周老师将秦九韶的《数书九章》、李治的《测圆海镜》《益古演段》、杨辉的《详解九章算法》、朱世杰的《算学启蒙》《四元玉鉴》这六部著作平均分给班级的3个数学兴趣小组，则分配方式一共有（    ）
A．15种 B．60种 C．80种 D．90种
【答案】D
【分析】先从6部中选2部，再从剩下的4部中选2部，此时把6部书分成3份，然后分给3个数学兴趣小组即可
【详解】解：由题意得，六部著作平均分给班级的3个数学兴趣小组的方法数有
.
故选:D.
8．（2023·全国·高三专题练习）甲乙丙丁四个同学星期天选择到东湖公园，西湖茶经楼，历史博物馆和北湖公园其中一处去参观游玩，其中茶经楼必有人去，则不同的参观方式共有（    ）种.
A．24 B．96 C．174 D．175
【答案】D
【分析】根据去茶经楼的人数进行分类讨论，结合排列组合知识进行求解.
【详解】若4人均去茶经楼，则有1种参观方式，
若有3人去茶经楼，则从4人中选择3人，另1人从另外3处景点选择一处，
有种参观方式；
若有2人去茶经楼，则从4人中选择2人，另外2人从另外3处景点任意选择一处，
有种参观方式；
若有1人去茶经楼，则从4人中选择1人，另外3人从另外的3处景点任意选择一处，
有种参观方式，
综上：共有种参观方式.
故选：D
9．（2023·全国·高三专题练习）2010年世界杯足球赛预计共有24个球队参加比赛，第一轮分成6个组进行单循环赛（在同一组的每两个队都要比赛），决出每个组的一、二名，然后又在剩下的12个队中按积分取4个队（不比赛），共计16个队进行淘汰赛来确定冠亚军，则一共需比赛（    ）场次．
A．53 B．52 C．51 D．50
【答案】C
【分析】分单循环赛和淘汰赛：单循环赛共需要场比赛，淘汰赛依次分别计算，在求总和即可．
【详解】第一轮分成6个组进行单循环赛共需要场比赛，淘汰赛有如下情况：16进8需要8场比赛，8进4需要4场比赛，4进2需要2场比赛，确定冠亚军需要1场比赛，共需要场比赛
故选：C．
10．（2023·全国·高三专题练习）教育部于2022年开展全国高校书记校长访企拓岗促就业专项行动，某市3所高校的校长计划拜访当地企业，共有4家企业可供选择.若每名校长拜访3家企业，每家企业至少接待1名校长，则不同的安排方法共有（    ）
A．60种 B．64种 C．72种 D．80种
【答案】A
【分析】按照间接法，先计算3名校长在4家企业任取3家企业的所有安排情况，然后减去3名校长选的3家企业完全相同的安排方法数，即可求得所需安排情况种数.
【详解】解：3名校长在4家企业任取3家企业的所有安排情况为：种
又每家企业至少接待1名校长，故3名校长选的3家企业，不全相同，
因为3名校长选的3家企业完全相同有种，
则不同的安排方法共有：种.
故选：A.
11．（2023·全国·高三专题练习）若分配甲、乙、丙、丁四个人到三个不同的社区做志愿者，每个社区至少分配一人，每人只能去一个社区．若甲分配的社区已经确定，则乙与甲分配到不同社区的概率是（    ）
A． B． C． D．
【答案】B
【分析】计算出甲单独去分配的社区，甲和乙，丙，丁三人的一人去分配的社区，从而得到总的分配方法，再计算出甲乙分配到同一舍去的方法，得到乙与甲分配到不同社区的方法，根据古典概型求概率公式进行计算.
【详解】甲单独去分配的社区，有将乙，丙，丁三人分为两组，再和另外两个社区进行全排列，有种方法；
甲和乙，丙，丁三人的一人去分配的社区，其余两人和另外两个社区进行全排列，有种方法；
其中甲乙分配到同一社区的方法有种，
则乙与甲分配到不同社区的方法有种，
所以乙与甲分配到不同社区的概率是
故选：B

二、多选题
12．（2022·全国·高三专题练习）已知，则的可能取值是（    ）
A．0 B．1 C．2 D．3
【答案】CD
【分析】将题设中的方程化为，从而可求的可能取值.
【详解】因为，所以，所以，
其中，而 ，
所以的值可能是2或3．
故选：CD．
13．（2023·全国·高三专题练习）某单位从6男4女共10名员工中，选出3男2女共5名员工，安排在周一到周五的5个夜晚值班，每名员工值一个夜班且不重复值班，其中女员工甲不能安排在星期一、星期二值班，男员工乙不能安排在星期二值班，其中男员工丙必须被选且必须安排在星期五值班，则（    ）
A．甲乙都不选的方案共有432种
B．选甲不选乙的方案共有216种
C．甲乙都选的方案共有96种
D．这个单位安排夜晚值班的方案共有1440种
【答案】ABC
【分析】本题考查排列组合的综合应用，对于A：从4男3女中，选出2男2女共4名员工排列；对于B：甲只能排星期三或星期四，从剩下的从4男3女中，选出2男1女共3名员工排列；对于C：分情况讨论：乙排星期一或乙不排星期一；对于D：分为四种情况：甲乙都不选、选甲不选乙、选乙不选甲和甲乙都选，重点分析运算选乙不选甲．
【详解】男员工丙必须被选且必须安排在星期五值班，则原题可理解为从5男4女共9名员工中，选出2男2女共4名员工，安排在周一到周四的4个夜晚值班，每名员工值一个夜班且不重复值班，其中女员工甲不能安排在星期一、星期二值班，男员工乙不能安排在星期二值班
甲乙都不选的方案共有种，A正确
选甲不选乙的方案共有种，B正确
甲乙都选，则分两种情况：乙排星期一或乙不排星期一
乙排星期一的方案共有种
乙不排星期一的方案共有种
∴甲乙都选的方案共有96种，C正确
这个单位安排夜晚值班分为四种情况：甲乙都不选、选甲不选乙、选乙不选甲和甲乙都选
选乙不选甲的方案共有种
∴这个单位安排夜晚值班的方案共有432+216+432+96=1176种，D错误
故选：ABC．
14．（2023·全国·高三专题练习）信息技术编程中会用到“括号序列”，一个括号序列是由若干个左括号和若干个右括号组成．合法括号序列可以按如下方式定义：①序列中第一个位置为左括号；②序列中左括号与右括号个数相同；③从序列第一个位置开始任意截取一个连续片段，该片段中左括号的个数不少于右括号的个数．例如（）（（））和（）（）都是合法括号序列，而（））（，）（）和（））（（）都不是合法括号序列．一个合法括号序列中包含的左括号和右括号的个数之和称为该序列的长度．若A和B都是括号序列，则AB表示将B拼接在A后得到的括号序列．根据以上信息，下列说法中正确的是（    ）
A．如果A，B是合法括号序列，则也是合法括号序列
B．如果是合法括号序列，则A，B一定都是合法括号序列
C．如果是合法括号序列，则A也是合法括号序列
D．长度为8的合法括号序列共有14种
【答案】AD
【分析】根据合法括号序列的定义可判断A；举反例可说明B,C的正误；分类讨论，考虑在前面四个位置上左括号的个数，算出符合条件的合法括号序列共有14种，判断D.
【详解】出题意知如果A，B是合法括号序列，则也是合法括号序列,A正确;
对于B,AB为（（））（）为合法括号序列，但取A为（（，B为））（）显然都不是合法括号序列，故B错误；
对于C, 如果是合法括号序列，比如（）（）为合法括号序列，
但A为）（，不是合法括号序列，故C错误；
对于D选项，由题意知第一个位置为左括号，最后一个位置为右括号，
分类考虑：（1）当前4个位置都为左括号时，则后4个位置都为右括号，故满足条件序列有1个；
（2）当前4个位置有3个左括号时，则第2，3，4个位置任取两个位置是左括号，第5，6，7个位置任取一个位置是右括号，故满足条件序列共有个；
（3）当前4个位置有2个左括号时，
则第2或第3个位置为左括号，第5个位置一定为左括号，第6，7个位置有一个为左括号，满足条件序列共有个，综上，共有个，D正确，
故选：AD．
15．（2023·全国·高三专题练习）为弘扬我国古代的“六艺文化”，某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程，每周一门，连续开设六周，则下列说法正确的是（    ）
A．某学生从中选2门课程学习，共有15种选法
B．课程“乐”“射”排在不相邻的两周，共有240种排法
C．课程“御”“书”“数”排在相邻的三周，共有144种排法
D．课程“礼”排在第一周，课程“数”不排在最后一周，共有96种排法
【答案】ACD
【分析】利用直接法、间接法、捆绑法以及分步乘法计数原理依次判断选项即可.
【详解】A：6门中选2门共有种选法，故A正确；
B：利用间接法，课程“乐”“射”排在相邻的两周时，把这两个看成一个整体，有种排法，然后全排列有种排法，根据分步乘法计数原理，“乐”“射”相邻的排法共有种，没有限制条件时共有种排法，故“乐”“射”排在不相邻的两周有种排法，故B错误；
C：课程“御”“书”“数”排在相邻的三周，即把这三个当作一个整体，有种排法，然后全排列有种排法，根据分步乘法计数原理，得共有种排法，故C正确；
D：先特殊后一般，先把“礼”排在第一周，再排“数”，有种排法，再把剩下4个全排列，有种排法，根据分步乘法计数原理，得共有种排法，故D正确.
故选：ACD.

三、解答题
16．（2022·全国·高三专题练习）（1）求值：
（2）求关于的不等式的解集．
【答案】（1）466；（2）
【分析】（1）根据题意可得，解之即可得解；
（2）根据组合数的运算公式计算即可得出答案.
【详解】解：（1）由可得：
，解得，
则；
（2）不等式，
即不等式，
解得，
又因，
所以关于的不等式的解集为.
17．（2023·全国·高三专题练习）已知五名同学，按下列要求进行排列，求所有满足条件的排列方法数.
(1)把5名同学排成一排且相邻；
(2)把5名同学排成一排且互不相邻；
(3)把5名同学安排到排成一排的6个空位中的5个空位上，且不相邻.
【答案】(1)；
(2)；
(3).

【分析】（1）根据给定条件，利用相邻问题捆绑法，列式求解作答.
（2）根据给定条件，利用不相邻问题插空法，列式求解作答.
（3）求出任取5个空位排5人的排法种数，减去A，B相邻的排法种数即可得解.
（1）
把A，B视为一个整体，不同排法有种，排A，B有种，
由分步乘法计数原理得：5名同学排成一排且相邻的排法种数是.
（2）
先排D，E有种，再把插入3个空隙中有种，
由分步乘法计数原理得：5名同学排成一排且互不相邻的排法种数是.
（3）
5名同学安排到排成一排的6个空位中的5个空位上的排法种数是，其中有一空位A，B相邻的排法种数是，
所以所求不同排法种数是：.
18．（2023·全国·高三专题练习）有名男生和甲、乙名女生排成一排，求下列情况各有多少种不同的排法？
(1)女生甲排在正中间；
(2)名女生不相邻；
(3)女生甲必须排在女生乙的左边（不一定相邻）；
(4)名女生中间恰有名男生．
【答案】(1)种；
(2)种；
(3)种；
(4)种.

【分析】（1）根据特殊元素优先排，其余元素再利用全排列即可求解；
（2）不相邻问题利用“插空法”即可求解；
（3）固定顺序问题即是所有元素全排列种类数的一半；
（4）相邻问题用“捆绑法”，其余元素再利用全排列即可.
（1）
女生甲排在正中间，其余人有种排法，因此不同排法种数为种；
（2）
将名男生排成一排，有种排法，2名女生可以在
每2名男生之间及两端共6个位置中选出2个排，有种排法，
因此不同排法种数为种；
（3）
对7名学生全排列有种排法，因此不同排法种数为种；
（4）
选1名男生排在2名女生中间，有种排法，将3人看成1个元素，
与4名男生共5个元素排成一排，不同的排法有种，
又因为2名女生有种排法，
因此不同排法种数为种.
题型三：二项式定理
一、单选题
1．（2023·全国·高三专题练习）的展开式中项的系数为（　　）
A． B． C．80 D．200
【答案】B
【分析】先利用二项式定理求出的展开式通项，再利用多项式相乘进行求解.
【详解】的展开式的通项为，
因为，
在中，令，得，
在中，令，得，
所以展开式中项的系数为.
故选：B.
2．（2023·全国·高三专题练习）展开式中，项的系数为（　　）
A．5 B．-5 C．15 D．-15
【答案】B
【分析】根据展开式的含义，可确定出现有两种情况，求出每种情况展开式中含有的项，即可求得答案.
【详解】，表示5个相乘，
展开式中出现有两种情况，第一种是中选出3个和2个1，
第二种是中选出4个和1个，
所以展开式中含有项有和，
所以项的系数为,
故答案为：B
3．（2022·北京市广渠门中学高三阶段练习）若的展开式中的第项和第项的二项式系数相等，则展开式中的系数为（    ）
A． B．
C． D．
【答案】B
【分析】根据第项和第项的二项式系数相等可构造方程求得，由此可得展开式通项，令即可求得的系数.
【详解】展开式中的第项和第项的二项式系数相等，，解得：，
展开式通项公式为：，
令，解得：，的系数为.
故选：B.
4．（2022·江苏省泰兴中学高三阶段练习）设，，则（    ）
A．
B．
C．
D．
【答案】A
【分析】将 运用二项式定理按照 和 展开，求出各项的系数，并用赋值法求出 和 的值，令 ，逐项验证即可求解.
【详解】由二项式定理知：
，
，令 ，则有 ；
，
，令 ，则有 ；
故有 ，A正确；
令 ，则有 ，
分别代入B，C，D选项：
，B错误；
，C错误；
，D错误；
故选：A.
5．（2022·江苏·金陵中学高三阶段练习）的展开式中的系数为（    ）
A． B． C． D．
【答案】B
【分析】由二项式定理将展开，然后得出，即可求出的系数.
【详解】由二项式定理：




观察可知的系数为.
故选：B.
6．（2022·江苏江苏·高三阶段练习）的展开式中的系数为（    ）
A． B． C． D．
【答案】D
【分析】根据二项式定理可分别求得和展开式中的系数，由此可得结果.
【详解】；
展开式中的系数为；展开式中的系数为；
展开式中的系数为.
故选：D.
7．（2023·广东茂名·高三阶段练习）下列各式中，不是的展开式中的项是（    ）
A． B． C． D．
【答案】D
【分析】根据题意多项式展开式中，有一个因式选，有2个因式选，其余的2个因式选，有1个因式选，剩下的3个因式选，分别计算所得项，即可得到结果.
【详解】表示4个因式的乘积，在这4个因式中，有一个因式选，其余的3个因式选，所得的项为，所以是的展开式中的项，在这4个因式中，有2个因式选，其余的2个因式选，所得的项为，所以是的展开式中的项，在这4个因式中，有1个因式选，剩下的3个因式选，所得的项为，所以是的展开式中的项，在这4个因式中，有2个因式选，其余的2个因式中有一个选，剩下的一个因式选，所得的项为，所以不是的展开式中的项.
故选:D.
8．（2023·全国·高三专题练习）在（）的展开式中，若第5项为二项式系数最大的项，则n的值不可能是（  ）
A．7 B．8 C．9 D．10
【答案】D
【分析】由题意，利用二项式系数的性质，求得的值．
【详解】当时，的展开式有8项，的展开式中二项式系数最大，
即第四项和第五项的二项式系数最大；
当时，的展开式有9项，的展开式中二项式系数最大，
即第五项的二项式系数最大；
当时，的展开式有10项，的展开式中二项式系数最大，
即第五项和第六项的二项式系数最大.
当时，的展开式有11项，的展开式中二项式系数最大，
即第六项的二项式系数最大.
故选：D．
9．（2023·全国·高三专题练习）在的展开式中，若二项式系数的和为，则的系数为（    ）
A． B． C． D．
【答案】A
【分析】根据二项式系数的和为，可得，再利用展开式的通项，即可得解．
【详解】二项式系数的和为，所以，展开式的通项为，令，则，
所以的系数为．
故选：A

二、多选题
10．（2023·全国·高三专题练习）已知，则下列结论正确的有（    ）
A． B．
C． D．
【答案】ABD
【分析】通过赋值根据选项一一判断即可得结果.
【详解】解：对于A，取得，所以，故A正确；
对于B，的展开式中第7项为，所以，故B正确；
对于C，取得，故C错误；
对于D，由，
取得，
取得，
所以，故D正确.
故选：ABD.
11．（2023·全国·高三专题练习）（多选）已知，则（    ）
A． B．
C． D．
【答案】CD
【分析】结合赋值法、二项式展开式的通项公式对选项进行分析，从而确定正确选项.
【详解】令，得，故A错误；
令，得，
即，所以，故B错误；
因为的展开式的通项为，
所以，故C正确；
由的展开式的通项及题意，
得，
令，得，
则，故D正确．
故选：CD
12．（2023·全国·高三专题练习）下列结论正确的是（    ）
A．命题“"的否定是""
B．已知回归模型为，则样本点的残差为
C．若样本数据的方差为2，则数据的方差为8
D．若的展开式中各项的二项式系数之和为32，则展开式中项的系数为
【答案】ABC
【分析】根据命题的否定可判断A，根据残差的计算即可判断B，根据方差的性质即可求解C，根据二项式系数和可求，再根据通项即可求解.
【详解】对于A,命题“"的否定是"",故正确；
对于B,当时，，故残差为，故正确，
对于C,由方差的性质可知：的方差为，故正确，
对于D,的展开式中各项的二项式系数之和为，故的通项为，令，故项的系数为，故错误，
故选：ABC
13．（2023·全国·高三专题练习）已知，则（    ）
A． B．
C． D．
【答案】BCD
【分析】赋值法即可求解所有项的系数和.根据二项式展开的通项特征可求指定项的系数.
【详解】令，得，故A错误；令得，即，故B正确；令，得，故C正确；展开式的通项为，令得，所以．故D正确．
故选:BCD．

三、解答题
14．（2023·全国·高三专题练习）在二项式的展开式中，二项式系数最大的项只有一项，且是第4项．
(1)求的值；
(2)求展开式中所有有理项的系数之和；
(3)把展开式中的项重新排列，求有理项互不相邻的排法种数．
【答案】(1)6
(2)32
(3)144

【分析】（1）利用二项式定理的展开式的性质即可求解；（2）利用二项式定理的展开式，找出的次数为整数的项，即可求解（3）元素不相邻的排列问题用插空法，即可求解.
（1）
由题意知，所以．
（2）
二项式的展开式的通项为，
当时，的次数为整数，对应的项为有理项．
于是展开式中有理项共有四项，分别为第1项第3项、第5项、第7项，
所以展开式中所有有理项的系数之和为（或）．
（3）
展开式共有7项，其中4项为有理项，3项为无理项．
将无理项排列，有种排法，
将有理项插空排列，有种排法，
故有理项互不相邻的排法共有（种）．
15．（2023·全国·高三专题练习）在①只有第5项的二项式系数最大；②第4项与第6项的二项式系数相等；③奇数项的二项式系数的和为128；这三个条件中任选一个，补充在下面（横线处）问题中，解决下面两个问题.
已知（n∈N*），___________
(1)求的值：
(2)求的值.
【答案】(1)-1
(2)16

【分析】(1)根据选①，②，③解得都有，所以有，
令，得，再令，得，于是可得；
(2)由(1)可得，所以有，两边分别求导得，再令即可得答案.
（1）
解：若选①：
因为只有第5项的二项式系数最大，
所以展开式中共有9项，即，得，
若选②：
因为第4项与第6项的二项式系数相等，
所以，
若选③：
因为奇数项的二项式系数的和为128，
所以，解得.
因为，
令，则有，
即有，
令，得，
所以；
综上所述：；
（2）
由(1)可知：无论选①，②，③都有，
，
两边求导得，
令，
则有，
所以.
16．（2023·全国·高三专题练习）已知展开式的二项式系数和为512，且.
(1)求的值；
(2)设，其中，且，求的值.
【答案】(1)
(2)

【分析】（1）根据二项展开式的二项式系数和求出，再结合，根据二项式定理即可求出答案；
（2）根据已知条件改写原式，得到原式可以被整除的部分，根据余项、转化求解即可得到答案.
（1）
因为展开式的二项式系数和为512，
所以，得，
所以，
所以.
（2）

，
因为能被6整除，
而，，所以.