中考数学专项训练（18）专题圆中不规则图形面积含解析答案

这是一份中考数学专项训练（18）专题圆中不规则图形面积含解析答案，共32页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

中考数学专项训练（18）专题 圆中不规则图形面积
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．如图，将边长为3的正六边形铁丝框（面积记为）变形为以点D为圆心，为半径的扇形（面积记为），则与的关系为（　　）

A． B． C． D．
2．如图，在扇形中，已知，，过的中点C作，，垂足分别为点D，E，则图中阴影部分的面积为（    ）

A． B． C． D．
3．如图，已知⊙O的半径是4，点A,B,C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（    ）

A． B． C． D．
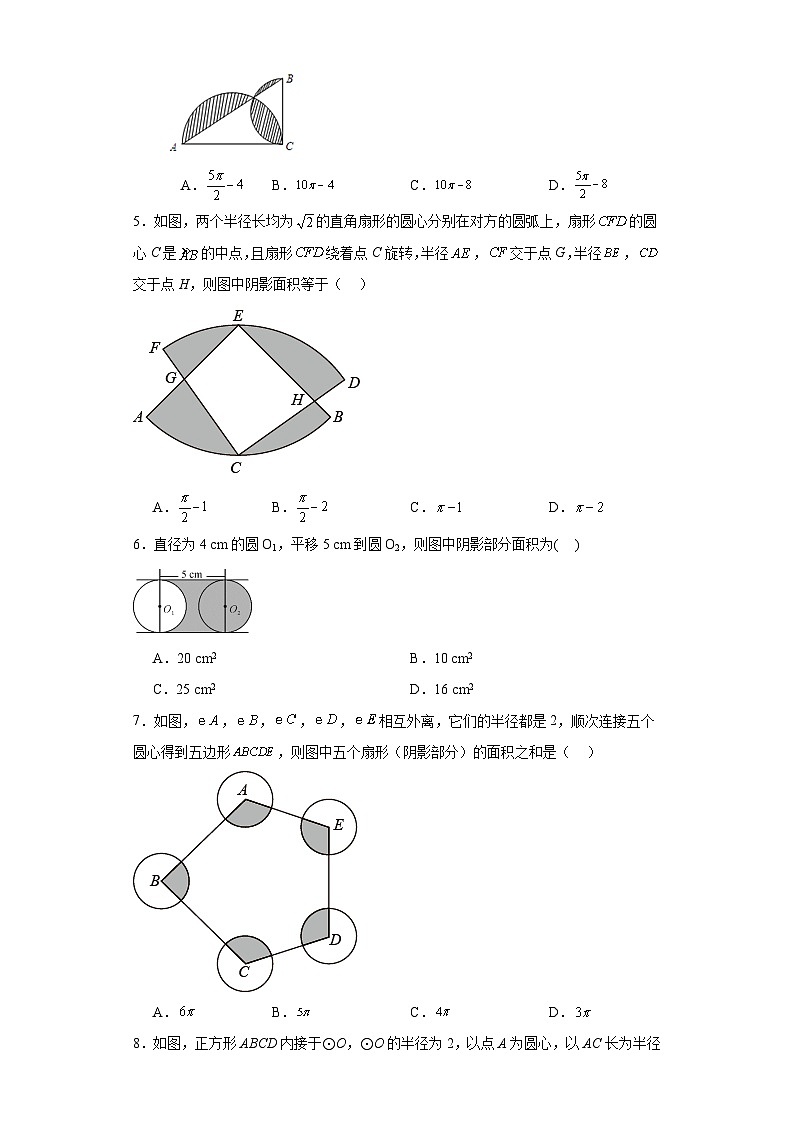
4．如图，在Rt中，∠BCA=90° 两分圆别以为半径画圆，则阴影部分的面积为（        ）

A． B． C． D．
5．如图，两个半径长均为的直角扇形的圆心分别在对方的圆弧上，扇形的圆心C是的中点，且扇形绕着点C旋转，半径，交于点G，半径，交于点H，则图中阴影面积等于（    ）

A． B． C． D．
6．直径为4 cm的圆O1，平移5 cm到圆O2，则图中阴影部分面积为(    )

A．20 cm2 B．10 cm2
C．25 cm2 D．16 cm2
7．如图，，，，，相互外离，它们的半径都是2，顺次连接五个圆心得到五边形，则图中五个扇形（阴影部分）的面积之和是（    ）

A． B． C． D．
8．如图，正方形ABCD内接于⊙O，⊙O的半径为2，以点A为圆心，以AC长为半径画弧交AB的延长线于点E，交AD的延长线于点F，则图中阴影部分的面积为（　　）

A．4π﹣4 B．4π﹣8 C．8π﹣4 D．8π﹣8
9．如图，在中，，，是的平分线，经过，两点的圆的圆心恰好落在上，分别与、相交于点、．若圆半径为2．则阴影部分面积（    ）．

A． B． C． D．

二、填空题
10．如图，在半径为的圆形纸片中，剪一个圆心角为90°的最大扇形（阴影部分），则这个扇形的面积为 ；若将此扇形围成一个无底的圆锥（不计接头），则圆锥底面半径为 ．

11．如图，在中，E为BC的中点，以E为圆心，BE长为半径画弧交对角线AC于点F，若，，，则扇形BEF的面积为 ．

12．如图，在中，，，则图中阴影部分的面积是 ．（结果保留）

13．如图，，，以点为圆心，为半径作弧交于点，点，交于点，若，则阴影部分的面积为 .

14．如图，A，C是双曲线上关于原点对称的点，B，D是双曲线上关于原点对称的点，圆弧与围成了一个封闭图形，当线段AC与BD都最短时，图中阴影部分的面积为 ．

15．如图，在⊙O中，直径，AC切于，交⊙O于，若，则阴影部分的面积为 .

16．如图，在Rt△ABC中，∠C＝90°，AB＝6，AD是∠BAC的平分线，经过A，D两点的圆的圆心O恰好落在AB上，⊙O分别与AB、AC相交于点E、F．若圆半径为2，则阴影部分面积＝ ．

17．如图，将四边形绕顶点A顺时针旋转至四边形的位置，若，则图中阴影部分的面积为 ．

18．如图，已知A(2，2)，B(2，1)，将△AOB绕着点O逆时针旋转，使点A旋转到点A′(－2，2)的位置，则图中阴影部分的面积为 ．

19．如图，AB是圆O的直径，弦CD⊥AB，∠BCD＝30°，CD＝4，则S阴影＝ ．

20．如图，在菱形中，对角线和交于点O，，，分别以点A、点C为圆心，以的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为 ．（结果保留）

21．如图，平行四边形ABCD中，AB=AC=4，AB⊥AC，O是对角线的交点，若⊙O过A、C两点，则图中阴影部分的面积之和为 ．

22．如图，P是半径为2的⊙O外一点，PB是⊙O的切线，B为切点，弦BC∥OA，且BC＝2，则图中阴影部分的面积为 ．


三、解答题
23．如图，在每个小正方形的边长为1的网格中，每个小正方形的顶点叫格点，的三个顶点均在格点上，把绕着点按逆时针方向旋转到．

（1）求的正切值．
（2）求扇形的面积．
24．某种冰激凌的外包装可以视为圆锥，它的底面圆直径与母线长之比为．制作这种外包装需要用如图所示的等腰三角形材料，其中，．将扇形围成圆锥时，，恰好重合．
（1）求这种加工材料的顶角的大小
（2）若圆锥底面圆的直径为5cm，求加工材料剩余部分（图中阴影部分）的面积．（结果保留）

25．如图，在中，BC＝4，且的面积为4，以点A为圆心，2为半径的⊙A交AB于E，交AC于F，点P是⊙A上一点，且∠＝45°．

（1）求证：BC为⊙A的切线；
（2）求图中阴影部分的面积．
26．如图，AB＝AC，⊙O为△ABC的外接圆，AF为⊙O的直径，四边形ABCD是平行四边形．
（1）求证：AD是⊙O的切线；
（2）若∠BAC＝45°，AF＝2，求阴影部分的面积．

27．如图，正方形的边长为a，以各边为直径在正方形内画半圆．求图中阴影部分的面积．

28．正三角形的边长为2，分别以A、B、C为圆心，以1为半径在三角形形内作弧，作内切圆，求阴影部分面积．

29．如图，是⊙O的直径，是⊙O上一点，平分，过点作交延长线于点．

（1）求证：是⊙O的切线；
（2）若，，求阴影部分的面积．
30．如图，在平面直角坐标系中，的三个顶点坐标分别为．

（1）作出关于原点对称的；
（2）将绕点逆时针旋转，根据三角形扫过的痕迹，求图中阴影部分的面积．
31．如图,在半径为2的⊙O中,点Q为优弧MN的中点,圆心角∠MON=60°,在弧QN上有一动点P,且点P到弦MN所在直线的距离为x.

(1)求弦MN的长;
(2)试求阴影部分面积y与x的函数关系式,并写出自变量x的取值范围;
(3)试分析比较,阴影部分面积y与的大小关系.

参考答案：
1．A
【分析】由正六边形的性质出的长，根据扇形面积公式=×弧长×半径，可得结果
【详解】解：由题意：
∴
∴
∴
故选：A
【点睛】本题考查了正多边形和圆、正六边形的性质、扇形面积公式；熟练掌握正六边形的性质，求出弧长是解决问题的关键．
2．B
【分析】根据矩形的判定定理得到四边形ODCE是矩形，连接OC，根据全等三角形的性质得到OD=OE，然后得到矩形ODCE是正方形，最后利用扇形和正方形的面积公式计算即可．
【详解】如图所示，连接OC

∵，，
∴四边形ODCE是矩形
∵点C是的中点
∴
∴
∴
∴四边形ODCE是正方形
∴
∴
∴
即
由扇形的面积公式可得：
∴
故选：B
【点睛】本题主要考查矩形的判定定理和性质、正方形的判定定理和性质、全等三角形的判定和性质、扇形面积的计算公式，熟练掌握相应的判定定理和性质是解题的关键．
3．B
【分析】连接OB和AC交于点D，根据菱形及直角三角形的性质先求出AC的长及∠AOC的度数，然后求出菱形ABCO及扇形AOC的面积，则由S扇形AOC-S菱形ABCO可得答案．
【详解】连接OB和AC交于点D，如图所示：

∵圆的半径为4，
∴OB=OA=OC=4，
又四边形OABC是菱形，
∴OB⊥AC，OD=OB=2，
在Rt△COD中利用勾股定理可知：CD=,
∵sin∠COD=
∴∠COD=60°，∠AOC=2∠COD=120°，
∴S菱形ABCO=,
∴S扇形=,
则图中阴影部分面积为S扇形AOC-S菱形ABCO=.
故选B.
【点睛】考查扇形面积的计算及菱形的性质，解题关键是熟练掌握菱形的面积=a•b（a、b是两条对角线的长度）；扇形的面积=.
4．A
【详解】设各个部分的面积为：，如图所示，
∵两个半圆的面积和是：，△ABC的面积是，阴影部分面积是：，
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积．
即阴影部分的面积=π×4+π×1-4×2÷2=π-4．
故选：A.

5．D
【分析】先根据扇形面积公式求出两扇形面积，再过C分别作CM⊥AE于M，CN⊥BE于N，连接EC，再证明△CMG≌△CNH，可证得白色部分的面积等于对角线为的正方形CMEN得面积，进而可求得阴影部分的面积．
【详解】解：∵两个直角扇形的半径长均为，
∴两个扇形面积和为，
过C分别作CM⊥AE于M，CN⊥BE于N，连接EC，则四边形CMEN是矩形，
∵C是的中点，
∴∠AEC=∠BEC，即EC平分∠AEB，
∴CM=CN，
∴四边形CMEN是正方形，
∴∠CMG=∠MCN=∠CNH，
∴∠MCG+∠GCN=∠NCH+∠GCN=90°，
∴∠MCG=∠NCH，
∴△CMG≌△CNH（ASA），
∴白色部分的面积等于对角线为的正方形CMEN的面积，
∴空白部分面积为，
∴阴影部分面积为，
故选：D．

【点睛】本题考查扇形面积公式、圆的有关性质、角平分线的性质、正方形的判定与性质、全等三角形的判定与性质，熟记扇形面积公式，熟练掌握角平分线的性质定理和全等三角形的判定与性质，求出空白部分面积是解答的关键．
6．A
【详解】分析：通过平移，把⊙O2的半圆向左平移到⊙O1的位置，则圆中阴影部分面积等于一个矩形的面积，然后根据面积公式计算即可．
详解：圆中阴影部分面积=5×4=20（cm2）．
故选A．
点睛：本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．
7．A
【分析】求出五个扇形的圆心角之和，利用扇形面积公式求解即可．
【详解】

故选A．
【点睛】本题考查了多边形内角和，扇形面积公式，理解题意是解题的关键．
8．A
【分析】利用对称性可知：阴影部分的面积=扇形AEF的面积-△ABD的面积.
【详解】利用对称性可知：阴影部分的面积=扇形AEF的面积-△ABD的面积=×4×2=4π-4，
故选：A．
【点睛】本题考查扇形的面积公式、正方形的性质等知识，解题的关键是学会用转化的思想思考问题．
9．C
【分析】连接OD，OF．首先证明OD∥AC，推出S阴＝S扇形OFA，再证明△AOF是等边三角形即可解决问题．
【详解】解：连接OD，OF．
∵AD是∠BAC的平分线，
∴∠DAB＝∠DAC，
∵OD＝OA，
∴∠ODA＝∠OAD，
∴∠ODA＝∠DAC，
∴OD∥AC，
∴∠ODB＝∠C＝90°，
∴S△AFD＝S△OFA，
∴S阴＝S扇形OFA，
∵OD＝OA＝2，AB＝6，
∴OB＝4，
∴OB＝2OD，
∴∠B＝30°，
∴∠A＝60°，
∵OF＝OA，
∴△AOF是等边三角形，
∴∠AOF＝60°，
∴S阴＝S扇形OFA＝.
故选：C．

【点睛】本题考查扇形的面积，等边三角形的判定和性质，解直角三角形等知识，解题的关键是添加常用辅助线，用转化的思想思考问题．
10． π
【分析】由勾股定理求扇形的半径，再根据扇形面积公式求值；根据扇形的弧长等于底面周长求得底面半径即可．
【详解】解：连接BC，
由∠BAC＝90°得BC为⊙O的直径，
∴BC＝2，
在Rt△ABC中，由勾股定理可得：AB＝AC＝2，
∴S扇形ABC＝＝π；
∴扇形的弧长为：＝π，
设底面半径为r，则2πr＝π，
解得：r＝，
故答案为：π，．

【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
11．
【分析】根据三角形内角和、三角形的外角以及等腰三角形性质求出，然后根据扇形面积公式计算．
【详解】解：∵，，
∴，
∵E为BC的中点，EB、EF为半径，
∴，
∴，
∵，
∴，
∴扇形BEF的面积．
【点睛】本题主要考查的是扇形面积计算，三角形内角和定理，等腰三角形性质，掌握扇形面积计算公式是解题的关键．
12．
【分析】由，根据圆周角定理得出，根据S阴影=S扇形AOB－可得出结论．
【详解】解：∵，
∴，
∴S阴影=S扇形AOB－

，
故答案为：．
【点睛】本题主要考查圆周角定理、扇形的面积计算，根据题意求得三角形与扇形的面积是解答此题的关键．
13．
【分析】根据题意连接OC，可得阴影部分的面积等于两个阴影部分面积之和，再根据弧AC所对的阴影部分面积等于弧AC所对圆心角的面积减去的面积，而不规则图形BCD的面积等于的面积减去弧DC所对圆心角的面积.进而可得阴影部分的面积.
【详解】解：根据题意连接OC


为等边三角形

阴影部分面积1=
阴影部分面积2=
阴影部分面积=阴影部分面积1+阴影部分面积2=
故答案为．
【点睛】本题只要考查圆弧的面积计算，关键在于阴影部分面积的分割.
14．
【分析】设点A，要使当线段AC与BD都最短，就是使OA最短，利用勾股定理表示出OA与x的函数解析式，将其函数解析式转化为顶点式，利用二次函数的性质可求出OA的最小值，即可求出AC的值；再利用同样的方法可求出BC的长；再证明△ABC是等边三角形，然后利用扇形的面积公式和三角形的面积公式可求出阴影部分的面积．
【详解】解：设点A， 要使当线段AC与BD都最短，就是使OA最短，
∴，
∴当时，OA的最小值为，
∴x=1（负值舍去），
∴点A（1，1），点；
∴AC=，
设点B ， 要使当线段BD都最短，就是使OB最短，
∴，
∴当时，OB的最小值为，
∴x=-（负值舍去），
∴点B ， 点D；
∵点B和点D，点A和点C关于原点对称，
∴BC=AB=CD=AD，
∴，
∴△ABC是等边三角形，
∴BC=AC=AB，
∴，
∴S阴影部分=．
故答案为：
【点睛】本题考查了反比例函数，线段最值，二次函数求最值，等边三角形，弓形面积的计算，解题关键在于求出线段的最值．
15．1
【分析】根据题意连接AD，得到ABC为等腰直角三角形，推出AB=BD，则弓形BD的面积=弓形AD的面积，故阴影部分的面积=△ACD的面积，可解出最终结果．
【详解】连接AD，，AC切⊙O于A点，
，ABC为等腰直角三角形，
又，AD=BD，
弓形BD的面积=弓形AD的面积，故阴影部分的面积=△ACD的面积，
AB=2，CD=AD=BD=，∴S△ACD=CD×AD==1，即阴影部分的面积是1．

【点睛】本题考查圆的性质及切线和弓形面积的知识，属于综合题，需要充分掌握圆的基础知识，学会运用圆的性质进行解题是关键．
16．
【分析】连接OD，OF．首先证明OD∥AC，推出S阴影＝S扇形OFA，再证明△AOF是等边三角形即可解决问题．
【详解】解：连接OD，OF．

∵AD是∠BAC的平分线，
∴∠DAB＝∠DAC，
∵OD＝OA，
∴∠ODA＝∠OAD，
∴∠ODA＝∠DAC，
∴OD∥AC，
∴∠ODB＝∠C＝90°，
∴S△AFD＝S△OFA，
∴S阴影＝S扇形OFA，
∵OD＝OA＝2，AB＝6，
∴OB＝4，
∴OB＝2OD，
∴∠B＝30°，
∴∠BAC＝60°，
∵OF＝OA，
∴△AOF是等边三角形，
∴∠AOF＝60°，
∴S阴影＝S扇形OFA＝．
故答案为：．
【点睛】本题考查扇形的面积，等边三角形的判定和性质，解直角三角形等知识，解题的关键是添加常用辅助线，运用转化的思想思考问题．
17．
【分析】由旋转的性质得：∠BAB'=45°，四边形AB'C'D'≌四边形ABCD，图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积-四边形AB'C'D'的面积=扇形ABB'的面积，代入扇形面积公式计算即可．
【详解】解：由旋转的性质得：∠BAB'=45°，四边形AB'C'D'≌四边形ABCD，
则图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积-四边形AB'C'D'的面积
=扇形ABB'的面积
=
=2π；
故答案为：2π．
【点睛】本题考查了旋转的性质、扇形面积公式；熟练掌握旋转的性质，得出阴影部分的面积=扇形ABB'的面积是解题的关键．
18．
【详解】试题分析：∵A（，2）、B（，1），∴OA=4，OB=，∵由A（，2）使点A旋转到点A′（﹣2，），∴∠A′OA=∠B′OB=90°，根据旋转的性质可得，，∴阴影部分的面积等于S扇形A'OA﹣S扇形C'OC==，故答案为．

考点：1．扇形面积的计算；2．坐标与图形变化-旋转．

19．
【分析】根据垂径定理求得，然后由圆周角定理知∠DOE=60°，然后通过解直角三角形求得线段OD、OE的长度，最后将相关线段的长度代入S阴影=S扇形ODB-S△DOE+S△BEC．
【详解】解：如图，设线段CD、AB交于点E，
∵AB是⊙O的直径，弦CD⊥AB，
∴CE＝ED＝2，
又∵∠BCD＝30°，
∴∠DOE＝2∠BCD＝60°，
∴∠ODE＝30°，
∴OE＝DE•tan∠ODE＝2×＝2，
∴OD＝2OE＝4，
∴S阴影＝S扇形ODB﹣S△DOE+S△BEC＝＝．
故答案为．

【点睛】此题考查了垂径定理、扇形面积的计算,解直角三角形，解题的关键是学会利用分割法求阴影部分面积，用转化的思想思考问题，属于中考常考题型．
20．
【分析】根据菱形的性质得到AC⊥BD，∠ABC=2∠ABD=60°，即可得出∠BAD=120°，根据直角三角形的性质求出AO、BD，根据扇形面积公式、三角形面积公式计算即可．
【详解】解：∵四边形ABCD是菱形，∠ABD=30°，
∴AC⊥BD，∠ABC=2∠ABD=60°，
∴∠BAD=120°，OA=AB=×4=2，
由勾股定理得，OB==，
∴BD=，
∴阴影部分的面积=××2-，
故答案为：．
【点睛】本题考查的是扇形面积计算、菱形的性质，掌握扇形面积公式是解题的关键．
21．4
【详解】解∶∵∠AOB=∠COD，
∴S阴影=S△AOB．
∵四边形ABCD是平行四边形，
∴OA=AC=×4=2．
∵AB⊥AC，
∴S阴影=S△AOB=OA•AB=×2×4=4．
【点睛】本题考查了平行四边形的性质，扇形面积的计算等知识，解题的关键是判断出阴影部分的面积等于△AOB的面积．
22．
【详解】整体分析：
连接OC，OB，则△OAB为等边三角形，由BC∥OA，得S△OCB＝S△PCB，把阴影部分的面积转化为扇形OBC的面积.
解：连接OC，OB.
∵OB＝OC＝BC＝2，
∴△OAB为等边三角形，
∴∠COB＝60°.
∵BC∥OA，
∴S△OCB＝S△PCB，
∴S阴影＝S扇形OBC＝＝.

23．（1）；（2）．
【分析】(1)过点C作CD⊥AB，交AB的延长线于D，如图,根据正切的定义求解；
(2)连接CC´，如图，先利用勾股定理的逆定理证明△ACC为直角三角形，则∠CAC=90°，然后根据扇形的面积公式计算．
【详解】解：（1）过点作，交的延长线于，

则，，
∴在中，．
（2）连接，
，，
∵，
∴为直角三角形，，
∴．
【点睛】本题考查了作图一旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
24．（1）=90°；（2）S阴影=（100-）cm2．
【分析】（1）设ED=x，则AD=2x，根据圆的周长求 弧长，利用弧长公式求即可；
（2）由，=90°，可得△ABC为等腰直角三角形，由可求BD=CD=AD=10cm， 利用三角形面积公式求S△BAC=，利用扇形面积公式求，利用面积差求S阴影即可．
【详解】解：（1）设ED=x，则AD=2x，
∴弧长，
∴，
∴=90°；
（2）∵ED=5cm，
∴AD=2ED=10cm，
∵，=90°，
∴△ABC为等腰直角三角形，
∵，
∴BD=CD=AD=10cm，
∴BC=BD+CD=20cm，
∴S△BAC=cm2，
∴，
∴S阴影= S△BAC-=（100-）cm2．
【点睛】本题考查圆锥，侧面展开图，扇形面积公式，等腰直角三角形判定与性质，利用割补法求阴影面积，掌握圆锥，侧面展开图，扇形面积公式，等腰直角三角形判定与性质，利用割补法求阴影面积是解题关键．
25．（1）证明见详解；（2）．
【分析】（1）作AD⊥BC，根据三角形的面积，可求出AD＝2=半径且为BC边上的高，即可判定；
（2）再根据圆周角定理得∠EAF＝2∠EPF＝90°，而＝，然后利用扇形的面积公式：S＝和三角形的面积公式即可计算出图中阴影部分的面积．
【详解】解：（1）过点A作AD⊥BC，如图，

∵BC=4，S△ABC=4，
∴，
∴AD=2，
又⊙A的半径为2，
∴BC与⊙A相切，切点为点D，
（2）∵由（1）可知⊙A与BC相切于点D，
∴AD⊥BC，且AD＝2，
又∵∠EPF＝45°
∴∠BAC=90°，
而BC＝4，，
∴＝＝BC×AD﹣＝．
【点睛】本题考查了扇形的面积公式：S＝（其中n为扇形的圆心角的度数，R为圆的半径），或S＝lR，l为扇形的弧长，R为半径．同时考查了切线的性质定理和圆周角定理．
26．（1）证明见解析；（2）．
【分析】（1）由题意根据垂径定理得到AF⊥BC，根据平行四边形的性质得到AD∥BC，求得AD⊥AF，于是得到AD是⊙O的切线；
（2）根据题意连接OC，OB，根据圆周角定理得到∠BOC=90°，根据勾股定理得到BC=，求得AD=BC=，连接OE，根据梯形和扇形的面积公式即可得到结论．
【详解】解：（1）∵AB＝AC，
∴，
∵AF为⊙O的直径，
∴AF⊥BC，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∠AD⊥AF，
∴AD是⊙O的切线；
（2）连接OC，OB，

∵∠BAC＝45°，
∴∠BOC＝90°，
∵AF＝2，
∴OB＝OC＝1，
∴BC＝，
∵四边形ABCD是平行四边形，
∴AD＝BC＝，
连接OE，
∵AB∥BD，
∴∠ACE＝∠BAC＝45°，
∴∠AOE＝2∠ACE＝90°，
∵OA＝OE＝1，
∴阴影部分的面积＝S梯形AOED﹣S扇形AOE＝（1+）×1﹣＝．
【点睛】本题考查切线的判定，等腰三角形的性质，平行四边形的性质，扇形的面积的计算，正确的作出辅助线是解题的关键．
27．
【分析】阴影部分的面积为正方形的面积减去四空白的面积．而正方形的面积减去两个半圆的面积就得两个空隙的面积，正方形的面积为a2，半圆的面积为 π.
【详解】解：如图，图中四个半圆都通过正方形的中心，用正方形的面积减去四空白的面积，剩下的就是阴影部分的面积，而正方形的面积减去两个半圆的面积就得两个空隙的面积，
∴，
∴
∴
【点睛】本题考查了圆的面积以及不规则的几何图形的面积的求法，将不规则图形转化为规则的几何图形的面积的和与差是解题的关键．
28．
【分析】根据切线长定理求出∠OBD=∠OBF=30°，由切线的性质得∠ODB=90°，根据勾股定理求出OD，然后根据S圆中间空白= 6S△BDO - 3S扇形BDF和S阴影=S⊙O- S圆中间空白求解即可．
【详解】解：连接OD，OB，由题意知BD=1，
∵△ABC是等边三角形，
∴∠ABC=60°，
∵⊙O是△ABC的内切圆，
∴∠OBD=∠OBF=30°，∠ODB=90°，
∴OB=2OD，
∵OD2+BD2=OB2，
∴OD2+12=4OD2，
∴OD=，
S圆中间空白= 6S△BDO - 3S扇形BDF
=
=，
∴S阴影=S⊙O- S圆中间空白
=
=．
故答案为：．

【点睛】本题考查了切线长定理，切线的性质，含30°角的直角三角形的性质，等边三角形的性质，勾股定理，以及扇形面积公式，熟练掌握各知识点是解答本题的关键．
29．（1）见解析；（2）
【分析】（1）连接OC，根据等腰三角形的性质得到∠BAC=∠ACO，推出ADOC，根据平行线的性质得到∠OCD=90°，于是得到CD是⊙O的切线；
（2）求出∠OEA=∠EOC=60°，由扇形的面积公式可得出答案．
【详解】（1）连接，
∵OC=OA，
∴∠BAC=∠ACO，
∵AC是∠BAD的平分线，
∴∠DAC=∠BAC，
∴∠DAC=∠ACO，
∴ADOC，
∴∠OCD+∠D=180°，
∵
∴∠CDA=90°，
∴∠OCD=90°，
∴CD是⊙O的切线．

（2）连接CE，OE，
∵，
∴，
∵，，
∴，
和为等边三角形

∴，
∴，
∴．

【点睛】本题考查了切线的判定与性质，等腰三角形的性质，扇形的面积的计算，正确的作出辅助线是解题的关键．
30．（1）所作图形如图所示，见解析；（2）图中阴影部分的面积为．
【分析】（1）根据关于原点对称的点的坐标特征得到A1、B1、C1，然后描点即可；
（2）由题意，阴影部分的面积等于线段绕点逆时针旋转90°所得到的扇形面积，即可求出答案．
【详解】解：（1）所作图形如图所示：

（2）由题意可知，
∵
所求阴影部分的面积等于线段绕点逆时针旋转90°所得到的扇形面积：
．
【点睛】本题考查了作图——旋转变换，旋转的性质，熟练掌握网格结构准确找出对应点的位置是解题的关键．也考查了三角形的面积和扇形面积公式．
31．（1）MN＝2；（2）；（3）见解析
【分析】（1）根据有一个角是60°的等腰三角形是等边三角形，可得出△OMN是等边三角形，即OM=ON=MN=2,（2）根据三角形的面积公式，即可列出y，x的函数关系式,
（3）根据等底等高的三角形的面积相等，可以过点O作OP′∥MN，以此线段为分界线进行分情况讨论．
【详解】(1)  ∵OM=ON,∠MON=60°,∴△MON是等边三角形,∴MN=OM=ON=2.
(2)  作OH⊥MN于H点,∴.在Rt△OHN中, ,

∴.,
∴,即.
(3)  令,即,∴.当时,;
当时,;当时,.
【点睛】本题主要考查了圆的综合题,解题时,利用了勾股定理、垂径定理、等边三角形的判定与性质以及扇形面积的计算,解决本题的关键是要熟练利用相关几何定理和性质.