初中数学苏科版八年级上册第三章 勾股定理3.1 勾股定理优秀课后测评

2023年苏科版数学八年级上册

《3.1 勾股定理》同步练习

一              、选择题

1.以下列各组数为三角形的边长，能构成直角三角形的是(    )

A.8，12， 17        B.1，2，3         C.6，8，10           D.5，12，9

2.如图，在正方形网格中，每个正方形的边长为1，则在△ABC中，边长为无理数的边数是(　　)

A.0         B.1        C.2        D.3

3.如图，在边长为1个单位长度的小正方形组成的网格中，点A，B都是格点，则以AB为边的正方形的面积为(  )

A.10    B.9    C.100    D.25

4.已知高为3，底边长为8的等腰三角形腰长为(   ).

A.3          B.4         C.5            D.6

5.如图，△ABC中，AB＝AC，AD是∠BAC的平分线.已知AB＝5，AD＝3，则BC的长为(  )

A.5            B.6                  C.8             D.10

6.已知直角三角形的两边分别为3和4，则第三边为(     )

A.5           B.           C.5或          D.4

7.如图所示，AB＝BC＝CD＝DE＝1，AB⊥BC，AC⊥CD，AD⊥DE，则AE＝(　　)

A.1      B.       C.       D.2

8.直角三角形的两边长分别是6，8，则第三边的长为(　　)

A.10                        B.2                       C.10或2                      D.无法确定

9.若直角三角形的三边长分别为2，4，x，则x的值可能有(    ).

A.1个    B.2个          C.3个      D.4个

10.直角三角形的三边为a﹣b，a，a＋b且a、b都为正整数，则三角形其中一边长可能为(　　)

A.61                         B.71                        C.81                             D.91

二              、填空题

11.若三角形三边之比为3：4：5，周长为24，则三角形面积           ．

12.在Rt△ABC中，∠C＝90o， AC＝6，BC＝8，则AB边的长是           .

13.在Rt△ABC中，∠C＝90°，∠A、∠B、∠C所对的边分别为a、b、c．

(1)若a＝2，b＝4，则c＝__________；

(2)若a＝2，c＝4，则b＝__________；

(3)若c＝26，a︰b＝5︰12，则a＝__________，b＝__________.

14.某直角三角形三条边的平方和为200，则这个直角三角形的斜边长为　　    ．

15.直角三角形三边长分别为3，4，a，则a＝     ．

16.按如图所示的方式作正方形和等腰直角三角形．若第一个正方形的边长AB＝1，第一个正方形与第一个等腰直角三角形的面积和为S1，第二个正方形与第二个等腰直角三角形的面积和为S2……则第n个正方形与第n个等腰直角三角形的面积和Sn＝          ．

三              、解答题

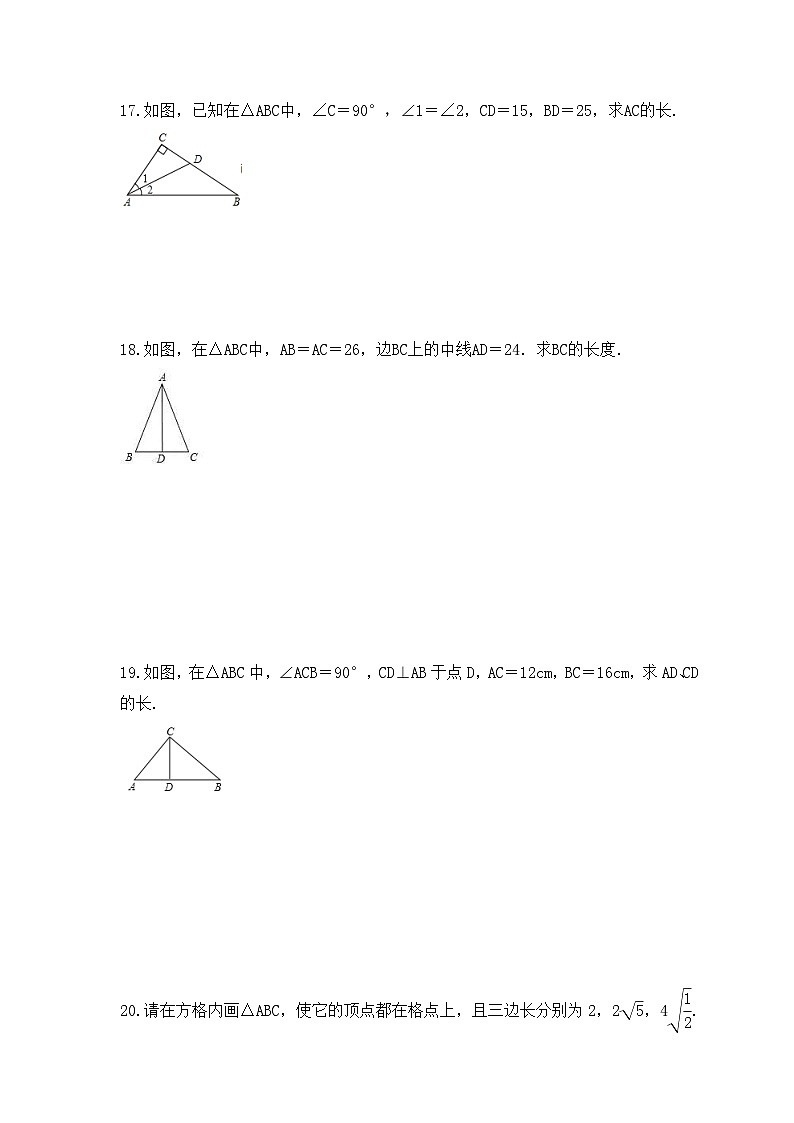
17.如图，已知在△ABC中，∠C＝90°，∠1＝∠2，CD＝15，BD＝25，求AC的长.

18.如图，在△ABC中，AB＝AC＝26，边BC上的中线AD＝24．求BC的长度．

19.如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，AC＝12cm，BC＝16cm，求AD、CD的长.

20.请在方格内画△ABC，使它的顶点都在格点上，且三边长分别为2，2，4.

(1)求△ABC的面积；

(2)求出最长边上的高.

21.如图，已知Rt△ABC中，∠ACB＝90°.请完成以下任务.

(1)尺规作图：①作∠A的平分线，交CB于点D；

②过点D作AB的垂线，垂足为点E.请保留作图痕迹，不写作法，并标明字母.

(2)若AC＝3，BC＝4，求CD的长.

22.如图，在等腰直角三角形ABC中，∠ABC＝90°，D为AC边中点，过D点做DE⊥DF，交AB于E，交BC于F．若AE＝4，FC＝3，求EF长.

答案

1.C

2.D.

3.A

4.C

5.C

6.C

7.D

8.C

9.B.

10.C.

11.答案为：24.

12.答案为：10.

13.答案为：(1)2；(2)2；(3)10，24.

14.答案为：10．

15.答案为：5或.

16.答案为：．

17.解：过D作DE⊥AB，垂足为E，

∵∠1＝∠2，

∴CD＝DE＝15，

在Rt△BDE中，BE＝20，

∵CD＝DE，AD＝AD，

∴Rt△ACD≌Rt△AED，

∴AC＝AE.

在Rt△ABC中，由勾股定理得AB2＝AC2＋BC2，

即(AC＋20)2＝AC2＋(15＋25)2，解得AC＝30.

18.解：∵在△ABC中，AB＝AC，AD是边BC上的中线，

∴AD⊥BC，BD＝DC．

∴AD2＋BD2＝AB2，

∵AD＝24，AB＝26，

∴BD2＝100，

∵BD＞0，

∴BD＝10，

∴DC＝10，

∴BC＝BD＋DC＝20．

19.解：∵∠ACB＝90°AC＝12cm，BC＝16cm，

∴AB＝20cm.

根据直角三角形的面积公式，得CD＝9.6cm.

在Rt△ACD中，AD＝7.2cm.

20.解：画图如图所示.

(1)S△ABC＝2.

(2)最长边上的高为.

21.解：(1)如图所示：①AD是∠A的平分线；

②DE是AB的垂线；

(2)在Rt△ABC中，由勾股定理得：

AB＝5，

由作图过程可知：DE＝DC，∠AED＝∠C＝90°，

∵S△ACD＋S△ABD＝S△ABC，

∴AC•CD＋AB•DE＝AC•BC，

∴×3×CD＋×5×CD＝×3×4，解得：CD＝.

22.解：连接BD．

∵D是AC中点，
∴∠ABD＝∠CBD＝45°，BD＝AD＝CD，BD⊥AC
∵∠EDB+∠FDB＝90°，∠FDB+∠CDF＝90°，
∴∠EDB＝∠CDF，
在△BED和△CFD中，
∠EBD＝∠C,BD＝CD,∠EDB＝∠CDF，
∴△BED≌△CFD(ASA)，
∴BE＝CF；
∵AB＝BC，BE＝CF＝3，
∴AE＝BF＝4，
在Rt△BEF中，EF＝.