广东省深圳市实验学校初中部2023—2024学年上学期十月月考九年级数学试卷（月考）

这是一份广东省深圳市实验学校初中部2023—2024学年上学期十月月考九年级数学试卷（月考），共7页。试卷主要包含了如图所示的工件，其俯视图是，当x＜0时，函数y＝﹣的图象在，已知点A，下面说法错误的是等内容，欢迎下载使用。
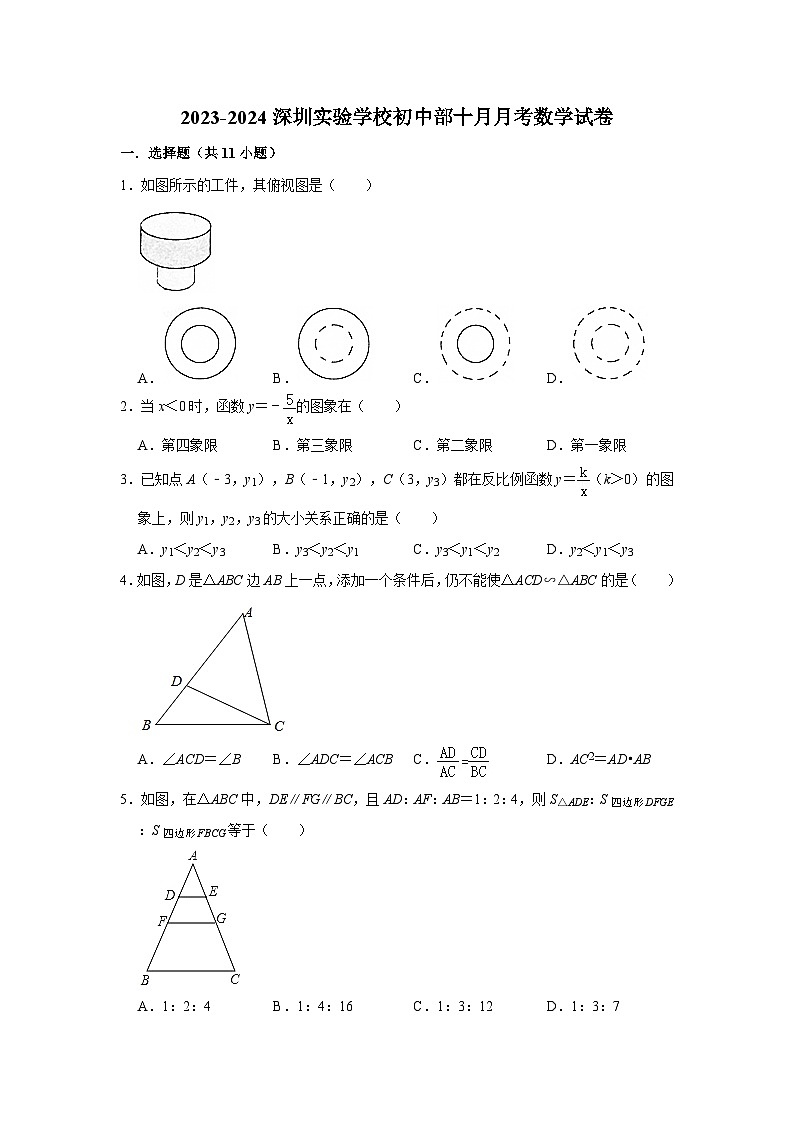
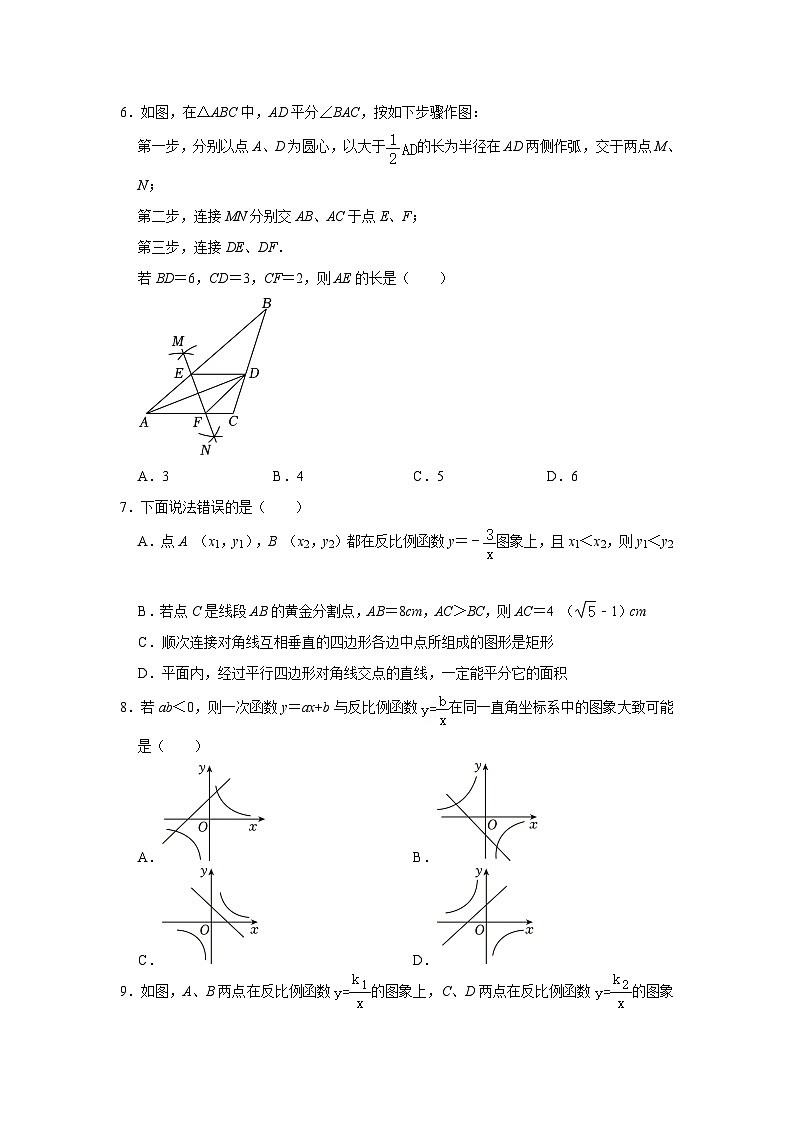
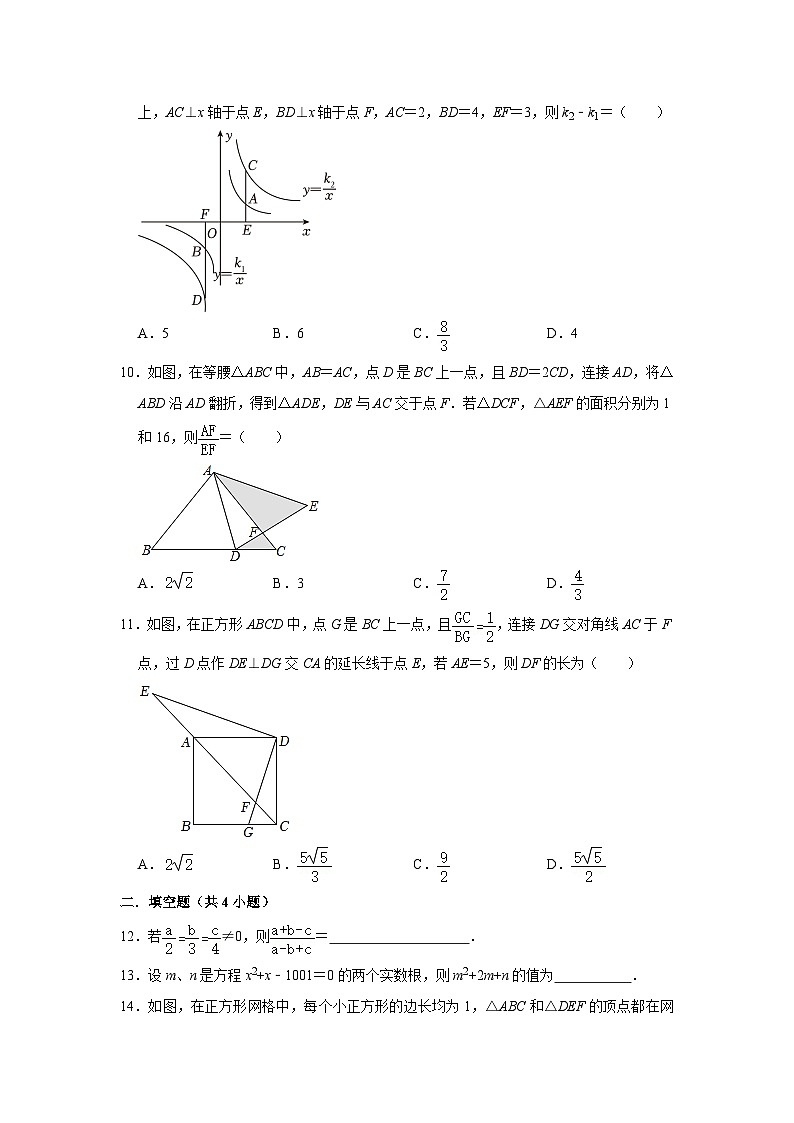
2023-2024深圳实验学校初中部十月月考数学试卷一．选择题（共11小题）1．如图所示的工件，其俯视图是（　　）A． B． C． D．2．当x＜0时，函数y＝﹣的图象在（　　）A．第四象限 B．第三象限 C．第二象限 D．第一象限3．已知点A（﹣3，y1），B（﹣1，y2），C（3，y3）都在反比例函数y＝（k＞0）的图象上，则y1，y2，y3的大小关系正确的是（　　）A．y1＜y2＜y3 B．y3＜y2＜y1 C．y3＜y1＜y2 D．y2＜y1＜y34．如图，D是△ABC边AB上一点，添加一个条件后，仍不能使△ACD∽△ABC的是（　　）A．∠ACD＝∠B B．∠ADC＝∠ACB C． D．AC2＝AD•AB5．如图，在△ABC中，DE∥FG∥BC，且AD：AF：AB＝1：2：4，则S△ADE：S四边形DFGE：S四边形FBCG等于（　　）A．1：2：4 B．1：4：16 C．1：3：12 D．1：3：76．如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于的长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN分别交AB、AC于点E、F；第三步，连接DE、DF．若BD＝6，CD＝3，CF＝2，则AE的长是（　　）A．3 B．4 C．5 D．67．下面说法错误的是（　　）A．点A （x1，y1），B （x2，y2）都在反比例函数y＝﹣图象上，且x1＜x2，则y1＜y2              B．若点C是线段AB的黄金分割点，AB＝8cm，AC＞BC，则AC＝4 （﹣1）cm C．顺次连接对角线互相垂直的四边形各边中点所组成的图形是矩形 D．平面内，经过平行四边形对角线交点的直线，一定能平分它的面积8．若ab＜0，则一次函数y＝ax+b与反比例函数在同一直角坐标系中的图象大致可能是（　　）A． B． C． D．9．如图，A、B两点在反比例函数的图象上，C、D两点在反比例函数的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC＝2，BD＝4，EF＝3，则k2﹣k1＝（　　）A．5 B．6 C． D．410．如图，在等腰△ABC中，AB＝AC，点D是BC上一点，且BD＝2CD，连接AD，将△ABD沿AD翻折，得到△ADE，DE与AC交于点F．若△DCF，△AEF的面积分别为1和16，则＝（　　）A． B．3 C． D．11．如图，在正方形ABCD中，点G是BC上一点，且，连接DG交对角线AC于F点，过D点作DE⊥DG交CA的延长线于点E，若AE＝5，则DF的长为（　　）A． B． C． D．二．填空题（共4小题）12．若≠0，则＝　                　．13．设m、n是方程x2+x﹣1001＝0的两个实数根，则m2+2m+n的值为　       　．14．如图，在正方形网格中，每个小正方形的边长均为1，△ABC和△DEF的顶点都在网格线的交点上．设△ABC的周长为C1，△DEF的周长为C2，则的值等于　                  　．15．如图，点A在双曲线y＝上，点C在双曲线y＝上，AC⊥x轴，过点A作AB⊥y轴，垂足为点B，连接AC，BC，BC与x轴交于点D，若BD＝2DC，△ABC面积为6，则k1+k2的值为　     　．三．解答题（共8小题）16．解下列方程：（1）2x2﹣3x﹣5＝0．（2）2（x﹣2）2＝x2﹣4．17．求值：（1﹣）÷﹣，其中x2+2x﹣1＝0．18．如图，在正方形网格中，点A、B、C都在格点上，利用格点按要求完成下列作图，（要求仅用无刻度的直尺，不要求写画法，保留必要的作图痕迹）（1）在图1中，以C为位似中心，位似比为1：2，在格点上将△ABC放大得到△A1B1C1；请画出△A1B1C1．（2）在图2中，线段AB上作点M，利用格点作图使得．（3）在图3中，利用格点在AC边上作一个点D，使得△ABD∽△ACB． 19．如图，一次函数y1＝ax+b的图象与反比例函数，k是常数，a≠0，k≠0）的图象交于第一象限C（1，4），D（4，m）两点，与坐标轴交于A、B两点，连接OC，OD．（O是坐标原点）（1）求一次函数y1与反比例函数y2的表达式；（2）直接写出当y2＞y1时x的取值范围；（3）将直线AB向下平移多少个单位长度，直线与反比例函数图象只有一个交点？20．在Rt△ABC中，∠BAC＝90°，AC＝12，AB＝16，点D是BC的中点，过点A作AE∥DC，且AE＝DC，连接CE．（1）求证：四边形ADCE是菱形；（2）连接DE交AC于点O，过点O作OF⊥DC．垂足为F，求DF的长． 21．芯片目前是全球紧缺资源，某市政府通过招商引进“芯屏汽合、集终生智”等优势产业，发展新兴产业，某芯片公司引进了一条内存芯片生产线，开工第一季度生产200万个，第三季度生产288万个．试回答下列问题：（1）已知每季度生产量的平均增长率相等，求前三季度生产量的平均增长率；（2）经调查发现，1条生产线最大产能是600万个/季度，若每增加1条生产线，每条生产线的最大产能将减少20万个/季度，现该公司要保证每季度生产内存芯片2600万个，在增加产能同时又要节省投入成本的条件下（生产线越多，投入成本越大），应该再增加几条生产线？ 22．【基础巩固】（1）如图1，在△ABC中，∠ACB＝90°，AC＝BC，D是AB边上一点，F是BC边上一点，∠CDF＝45°．求证：AC•BF＝AD•BD；【尝试应用】（2）如图2，在四边形ABFC中，点D是AB边的中点，∠A＝∠B＝∠CDF＝45°，若AC＝9，BF＝8，求线段CF的长．【拓展提高】（3）在△ABC中．AB＝4，∠B＝45°，以A为直角顶点作等腰直角三角形ADE，点D在BC上，点E在AC上．若CE＝2，求CD的长．        23．综合与实践问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为△ABC和△DFE，其中∠ACB＝∠DEF＝90°，∠A＝∠D，将△ABC和△DFE按图2所示方式摆放，其中点B与点F重合（标记为点B）．当∠ABE＝∠A时，延长DE交AC于点G，试判断四边形BCGE的形状，并说明理由．数学思考：（1）请你解答老师提出的问题；深入探究：（2）老师将图2中的△DBE绕点B逆时针方向旋转，使点E落在△ABC内部，并让同学们提出新的问题．①“善思小组”提出问题：如图3，当∠ABE＝∠BAC时，过点A作AM⊥BE交BE的延长线于点M，BM与AC交于点N．试猜想线段AM和BE的数量关系，并加以证明．请你解答此问题；②“智慧小组”提出问题：如图4，当∠CBE＝∠BAC时，过点A作AH⊥DE于点H，若BC＝9，AC＝12，求AH的长．请你思考此问题，直接写出结果．