广东省佛山市顺德区华侨中学2023-2024学年高二上学期10月月考数学试题（月考）

这是一份广东省佛山市顺德区华侨中学2023-2024学年高二上学期10月月考数学试题（月考），共13页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
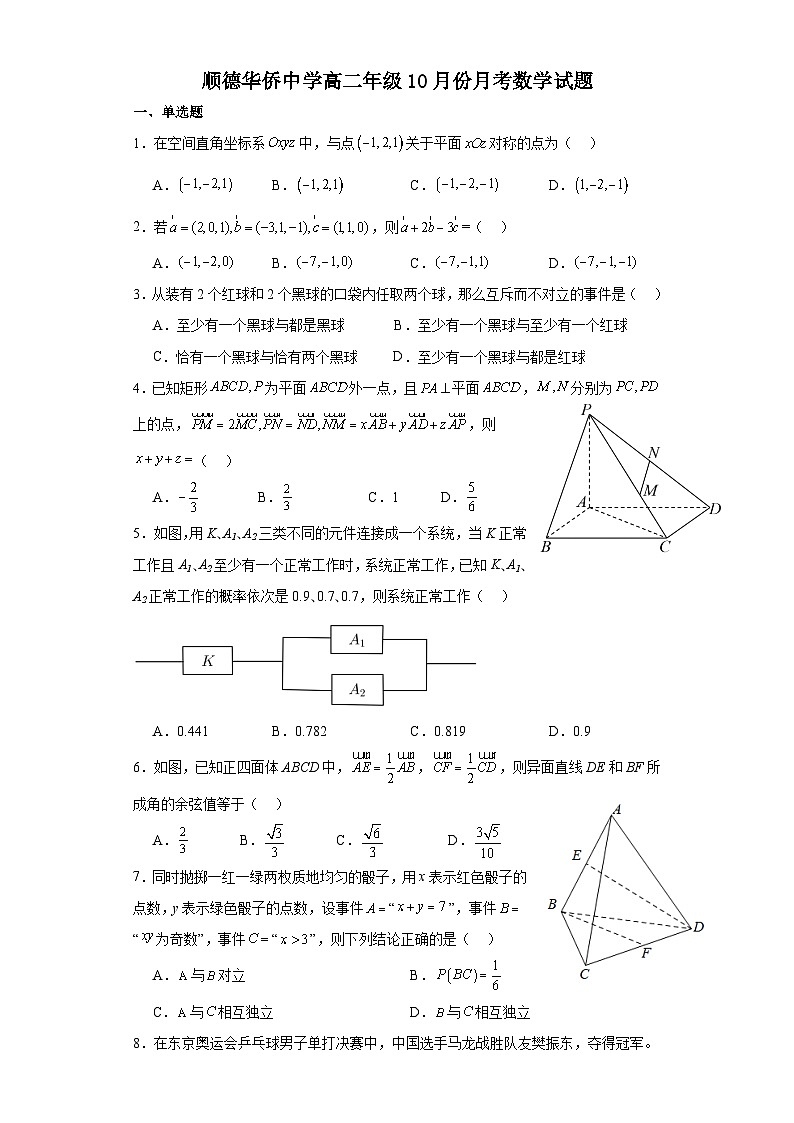
顺德华侨中学高二年级10月份月考数学试题一、单选题1．在空间直角坐标系中，与点关于平面对称的点为（    ）A． B． C． D．2．若，则=（    ）A． B． C． D．3．从装有2个红球和2个黑球的口袋内任取两个球，那么互斥而不对立的事件是（    ）A．至少有一个黑球与都是黑球       B．至少有一个黑球与至少有一个红球C．恰有一个黑球与恰有两个黑球     D．至少有一个黑球与都是红球4．已知矩形为平面外一点，且平面，分别为上的点，，则（    ）A． B． C．1      D．5．如图，用K､A1､A2三类不同的元件连接成一个系统，当K正常工作且A1､A2至少有一个正常工作时，系统正常工作，已知K､A1､A2正常工作的概率依次是0.9､0.7､0.7，则系统正常工作（    ）A．0.441 B．0.782 C．0.819 D．0.96．如图，已知正四面体ABCD中，，，则异面直线DE和BF所成角的余弦值等于（    ）A． B． C． D．7．同时抛掷一红一绿两枚质地均匀的骰子，用x表示红色骰子的点数，y表示绿色骰子的点数，设事件“”，事件“为奇数”，事件“”，则下列结论正确的是（    ）A．与对立 B．C．与相互独立 D．与相互独立8．在东京奥运会乒乓球男子单打决赛中，中国选手马龙战胜队友樊振东，夺得冠军。乒乓球决赛采用7局4胜制.在决胜局的比赛中，先得11分的运动员为胜方，但打到10平以后，先多得2分者为胜方.在平后，双方实行轮换发球法，每人每次只发1个球.若在决胜局比赛中，马龙发球时马龙得分的概率为，樊振东发球时马龙得分的概率为，各球的结果相互独立，在双方平后，马龙先发球，则双方战至的概率为（    ）A． B． C． D．二、多选题9．已知，，是不共面的三个向量，则能构成空间的一个基底的一组向量是（    ）A．+，-2， B．-， +3，2C．，2，- D．+，-，10．已知事件，，且，，则下列结论正确的是（    ）A．如果，那么，B．如果与互斥，那么，C．如果与相互独立，那么，D．如果与相互独立，那么，11．已知空间中三点，，，则下列说法正确的是（    ）A．与是共线向量 B．与同向的单位向量是C．和夹角的余弦值是 D．平面的一个法向量是12．长方体中，，，点分别在棱和上运动（不含端点），若，下列说法正确的是（    ）A． B．的最大值为C．面积的最大值为 D．三棱锥的体积不变三、填空题13．已知向量，，若与垂直，则＝     .14．某兴趣小组有2名男生和3名女生，现从中任选2名学生去参加活动，则恰好选中2名女生的概率为        ．15．已知空间三点，，，若直线上一点，满足，则点的坐标为           ．16．已知球内切于正四面体，且正四面体的棱长为，线段是球的一条动直径（，是直径的两端点），点是正四面体的表面上的一个动点，则的最大值是  ．四、解答题17．一个不透明的袋子中装有除颜色外完全相同的5个球，其中有3个红球，编号分别为A，B，C，有2个黑球，编号分别为D，E，从中一次摸取1个球，取后不放回，连续取两次．(1)试写出该试验的样本空间；(2)设事件M：“第一次摸到红球”，事件N：“第二次摸到黑球”，求事件M和事件N发生的概率． 18．已知空间三点，，．（1）求的面积；（2）若向量，且，求向量的坐标． 19．某种有奖销售的饮料，瓶盖内印有“奖励一瓶”或“谢谢购买”字样，购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖，中奖概率为.甲、乙、丙三位同学每人购买了一瓶该饮料．（Ⅰ）求三位同学都没有中奖的概率；（Ⅱ）求三位同学中至少有两位没有中奖的概率. 20．如图，已知三棱柱，平面平面，，分别是的中点．（1）证明：；（2）求直线与平面所成角的正弦值．  21．随着小汽车的普及，“驾驶证”已经成为现代人“必考”证件之一，若某人报名参加了驾驶证考试，要顺利地拿到驾驶证，需要通过四个科目的考试，其中科目二为场地考试．在每一次报名中，每个学员有5次参加科目二考试的机会（这5次考试机会中任何一次通过考试，就算顺利通过，即进入下一科目考试，若5次都没有通过，则需要重新报名），其中前2次参加科目二考试免费，若前2次都没有通过，则以后每次参加科目二考试都需要交200元的补考费，某驾校通过几年的资料统计，得到如下结论：男性学员参加科目二考试，每次通过的概率均为，女性学员参加科目二考试，每次通过的概率均为，现有这个驾校的一对夫妻学员同时报名参加驾驶证科目二考试，若这对夫妻每人每次是否通过科目二考试相互独立，他们参加科目二考试的原则为：通过科目二考试或者用完所有机会为止．(1)求这对夫妻在本次报名参加科目二考试通过且都不需要交补考费的概率；(2)求这对夫妻在本次报名参加科目二考试通过且产生的补考费用之和为200元的概率．   22．在三棱柱中，侧面正方形的中心为点平面，且，点满足．(1)若平面，求的值；(2)求点到平面的距离；(3)若平面与平面所成角的正弦值为，求的值．
顺德华侨中学高二年级10月份月考数学试题参考答案：1．A【详解】解：因为点，则其关于平面对称的点为.故选：A.2．D【详解】.故选：D3．C【详解】对于：事件：“至少有一个黑球”与事件：“都是黑球”可以同时发生，如：两个都是黑球，这两个事件不是互斥事件，不正确；对于：事件：“至少有一个黑球”与事件：“至少有一个红球”可以同时发生，如：一个红球一个黑球，不正确；对于：事件：“恰好有一个黑球”与事件：“恰有两个黑球”不能同时发生，但从口袋中任取两个球时还有可能是两个都是红球，两个事件是互斥事件但不是对立事件，正确；对于：事件：“至少有一个黑球”与“都是红球”不能同时发生，但一定会有一个发生，这两个事件是对立事件，不正确；故选：.4．B【详解】因为，所以，故，故.故选：B5．C【详解】并联的元件正常工作的概率为，故系统正常工作的概率为，故选：C.6．A【详解】在正四面中，设向量，， ，则三个向量两两夹角为，设正四面体的棱长等于1，且，，，∵，，∴ ，，，，∵，∴，即直线和所成角的余弦值为，故选：A.7．C【详解】依题意，样本空间为： 共36种，事件包含的基本事件为： 共种，，事件包含的基本事件为： 共种，，事件包含的基本事件为：共种，对于A，事件与事件互斥，不对立，A错误；事件与事件同时发生的基本事件为：，共种，，B错误；事件与事件同时发生的基本事件为：，共种，，对于C，，C正确；对于D，，D错误.故选C.8．A【详解】记甲为马龙，乙为樊振东在比分为后甲先发球的情况下，甲以赢下此局分两种情况：①后四球胜方依次为甲乙甲甲，概率为：.②后四球胜方依次为乙甲甲甲，概率为，，乙以赢下此局分两种情况：③后四球胜方依次为乙甲乙乙，概率为：④后四球胜方依次为甲乙乙乙，概率为，所以，所求事件概率为.故选：A9．AC【详解】A. 设+=x（-2）+y= ，则无解，所以+，-2，不共面，故正确；  B. 设-=x（+3）+2y= ，则 ，解得，所以-， +3，2共面，故错误；C. 设=2x）+y= ，则 ，无解，所以，2，-不共面，故正确；D. 设+=x（-）+y= ，则 ，解得，所以+，-，共面，故错误；故选：AC10．BD【详解】解：A选项：如果，那么，，故A选项错误；B选项：如果与互斥，那么，，故B选项正确；C选项：如果与相互独立，那么，，故C选项错误；D选项：如果与相互独立，那么，，故D选项正确.故选：BD.11．BD【详解】对于A，，，可知，与不共线，A错误；对于B，，，，即与同向的单位向量是，B正确；对于C，，，即和夹角的余弦值为，C错误；对于D，设平面的法向量，则，令，解得：，，，即平面的一个法向量为，D正确.故选：BD.12．ACD【详解】如图，  以为原点，为轴，为轴，为轴建立空间直角坐标系，设（），（），则，，，，，，，由得.选项，由，所以，所以，选项正确；选项B，，因为，所以，即没有最大值，选项B错误；选项C，由得，所以当时，取得最大值，所以面积，选项C正确；选项，面积是定值，到平面的距离为定值，所以三棱锥的体积为定值，又因为，所以三棱锥的体积不变，选项D正确.故选：ACD13．【详解】向量与垂直，则有，解得，于是，所以.故答案为：14．详解：从5名学生中抽取2名学生，共有10种方法，其中恰好选中2名女生的方法有3种，因此所求概率为15．【详解】依题意，得，设，则，所以，若，则，即，解得，即．故答案为：16．8【详解】解：由正四面体棱长为，其内切圆的半径为，由题意，，是直径的两端点，可得，，则，当点在正四面体顶点时，最大，且最大值为，则的最大值为，故答案为：．17．【详解】（1）试验从中一次摸取1个球，取后不放回，连续取两次的样本空间为：（2）由（1）可知样本空间中基本事件总数为符合事件M：“第一次摸到红球”的样本空间为：共个基本事件符合事件N：“第二次摸到黑球”的样本空间为：共个基本事件故，则事件M和事件N发生的概率分别为.18．【详解】（1）设向量，的夹角为，由已知，，，，，∵，∴，∴．（2）∵，∴，，∵，即，即，∴，即，或．19．【详解】设甲、乙、丙三位同学中奖分别为事件A、B、C，那么事件A、B、C相互独立，且P(A)=P(B)=P(C)．(1)三位同学都没有中奖的概率为：P(··)=P()P()P()． (2)三位同学中至少有两位没有中奖的概率为：P=．20．【详解】（1）如图所示，连结，等边中，，则，平面平面，且平面平面，由面面垂直的性质定理可得：平面，故，由三棱柱的性质可知，而，故，且，由线面垂直的判定定理可得：平面，结合平面，故.    （2）在底面内作，以点为坐标原点，方向分别为轴正方向建立空间直角坐标系设，则，，，据此可得：，由可得点的坐标为，利用中点坐标公式可得：，由于，故直线的方向向量为：， 设平面的法向量为，则：据此可得平面的一个法向量为，此时，设直线与平面所成角为，则.21．【详解】（1）分别表示丈夫和妻子第i次通过考试的事件，则，夫妻二人都不需要交补考费的事件，则，所以这对夫妻在本次报名参加科目二考试通过且都不需要交补考费的概率是.（2）由（1）知，夫妻二人共交200元补考费的事件，则，所以这对夫妻在本次报名参加科目二考试通过且产生的补考费用之和为200元的概率.22．【详解】（1）在三棱柱中，因，即点在上，连接ME，如图，  因平面面，面面，则有，而为中点，于是得为的中点，所以.（2）在三棱柱中，面面，则点到平面的距离等于点到平面的距离，又为正方形，即，而平面，以为原点，的方向分别为轴正方向建立空间直角坐标系，如图，依题意，，则，，设平面的法向量为，则，令，得，又，则到平面的距离，所以点到平面的距离为.（3）因，则，，设面的法向量为，则，令，得，于是得，而平面与平面所成角的正弦值为，则，即，整理得，解得或，所以的值是或.