新教材2023_2024学年高中物理第1章磁吃电流的作用本章整合课件教科版选择性必修第二册

这是一份新教材2023_2024学年高中物理第1章磁吃电流的作用本章整合课件教科版选择性必修第二册，共31页。

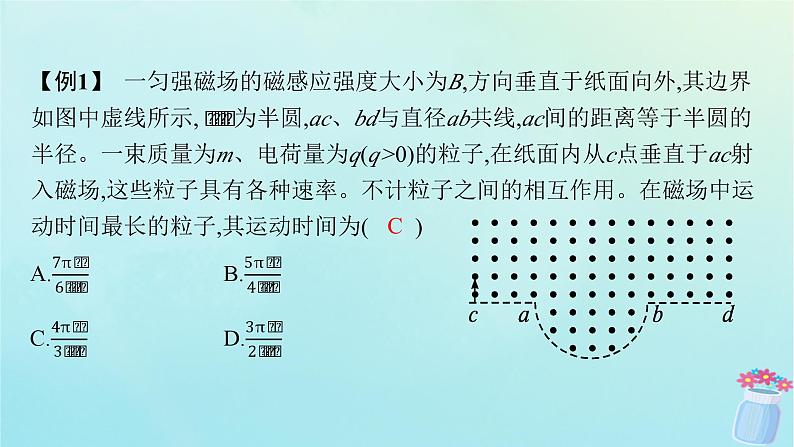
第一章本章整合突破一　带电粒子在磁场中运动的周期性多解问题和临界问题带电粒子在磁场中做圆周运动引起多解的原因:(1)带电粒子的电性不确定形成多解,可能出现两个方向的运动轨迹。(2)磁场方向不确定形成多解,可能出现两个方向的运动轨迹。(3)临界状态不唯一形成多解,需要根据临界状态的不同分别求解。(4)圆周运动的周期性形成多解。【例1】 一匀强磁场的磁感应强度大小为B,方向垂直于纸面向外,其边界如图中虚线所示, 为半圆,ac、bd与直径ab共线,ac间的距离等于半圆的半径。一束质量为m、电荷量为q(q>0)的粒子,在纸面内从c点垂直于ac射入磁场,这些粒子具有各种速率。不计粒子之间的相互作用。在磁场中运动时间最长的粒子,其运动时间为(　　)C解析 带电粒子在半圆形磁场中运动的最长时间为六分之一周期。粒子在磁场中做匀速圆周运动粒子在磁场中运动的时间 ,则粒子在磁场中运动的时间与速度无关,轨迹对应的圆心角越大,运动时间越长。设轨迹交 于e点,连接ce,则β为水平直径下方轨迹的对应的圆周角,故θ=π+2β,当β最大时,θ有最大值。由几何关系知,当ce与 相切时,β最大,此时β=30°,即轨迹对应的最大圆心角对点演练1(2023山东日照高二期末)某型号带电粒子的约束装置如图所示。分界面P、M、N、Q将某一区域分为Ⅰ、Ⅱ、Ⅲ三部分,P、M、N、Q所在平面相互平行,以O点为坐标原点,水平直线为x轴,规定向右为正方向,x轴与界面P、M、N、Q的交点分别为O、O1、O2、O3,以平行于P水平向里为z轴正方向,竖直向上为y轴正方向,建立空间直角坐标系Oxyz。区域Ⅰ内充满沿y轴负方向的匀强电场,电场强度E=5×103 N/C;区域Ⅱ内充满沿y轴负方向的匀强磁场,磁感应强度B1=2×10-2 T;区域Ⅲ内充满沿x轴正方向的匀强磁场,磁感应强度B2= T。一比荷 =5×107 C/kg的带正电粒子,在Oxy平面内,从O点以速度v0进入电场,速度大小v0=4×105 m/s,速度方向与x轴正方向夹角θ=60°,粒子经过界面M上的A点平行于x轴方向进入MN间的磁场,不计粒子重力。sin 53°=0.8,cos 53°=0.6。(1)求A点的坐标。(2)若粒子不能进入N、Q间的磁场,求MN间的最小距离dmin。(3)若MN间的距离d=0.16 m,NQ间的距离 ,粒子经过界面上的F点(图中未画出),求F点到O3的距离。答案 (1)(0.16 m,0.24 m,0)　(2)0.2 m　(3)0.08 m解析 (1)由题意可知,粒子在Oxy平面内,从O点以速度v0进入电场做类斜抛运动,y方向上做匀减速运动,有qE=ma-(v0sin 60°)2=-2ay联立解得y=0.24 m粒子在电场中运动的时间x方向上做匀速运动x=v0t1cos θ=0.16 mz=0所以A点的坐标为(0.16 m,0.24 m,0)。(2)粒子经过界面M上的A点后,速度为v=v0cos θ=2×105 m/s沿水平方向进入MN间的磁场,在Oxz水平面内做匀速圆周运动。根据洛伦兹力充当向心力可得得R1=0.2 m若粒子不能进入N、Q间的磁场,MN间的最小距离dmin=R1=0.2 m。(3)若MN间的距离为0.16 m,粒子将从N上的C点进入N、Q间的匀强磁场中,如图所示,粒子在C点速度方向与x轴方向的夹角为α得α=53°由分析可知粒子将在Oyz平面内做匀速圆周运动,在x方向上做匀速直线运动,即等距螺旋运动vx=vcos 53°=1.2×105 m/svz=vsin 53°=1.6×105 m/s圆心为D,运动轨迹在Q所在平面的投影如图所示 A点与C点在z方向的水平距离l1=R1-R1cos 53°=0.08 m带电粒子从N到Q所用时间为t2=解得t2=2.25π×10-6 s粒子在Oyz平面内做匀速圆周运动的角速度转过的角度φ=ωt2=3π粒子转过1.5圈打到界面Q上的F点CF=0.24 m故F点与O3均在Oxz平面,可得O3F=l1=0.08 m。突破二　磁聚焦和磁发散问题1.带电粒子的会聚 甲 如图甲所示,大量同种带正电的粒子,速度大小相同,平行入射到圆形磁场区域,如果轨迹圆半径与磁场圆半径相等(R=r),则所有的带电粒子将从磁场圆的最低点B点射出。证明:四边形OAO'B为菱形,必是平行四边形,对边平行,OB必平行于AO'(即竖直方向),可知从A点发出的带电粒子必然经过B点。2.带电粒子的发散如图乙所示,有界圆形磁场的磁感应强度为B,圆心为O,从P点有大量质量为m、电荷量为q的正电粒子,以大小相等的速度v沿不同方向射入有界磁场,不计粒子的重力,如果正电粒子轨迹圆半径与有界圆形磁场半径相等,则所有粒子射出磁场的方向平行。乙 证明:所有粒子运动轨迹的圆心与有界圆圆心O、入射点、出射点的连线为菱形,也是平行四边形,O1A、O2B、O3C均平行于PO,即出射速度方向相同(水平方向)。【例2】 (多选)如图所示是半径为R、磁感应强度为B的圆形匀强磁场,MN是一竖直放置的足够长的感光板。大量相同的带正电粒子从圆形磁场最高点P以速率v沿不同方向垂直磁场方向射入,不考虑速度沿圆形磁场切线方向入射的粒子。粒子质量为m,电荷量为q,不考虑粒子间的相互作用和粒子的重力。关于这些粒子的运动,下列说法正确的是(　　)A.对着圆心入射的粒子,速度越大,在磁场中运动的时间越短B.对着圆心入射的粒子,速度越大,在磁场中运动的时间越长C.若粒子速度大小均为v= ,出射后均可垂直打在MN上D.若粒子速度大小均为v= ,则粒子在磁场中的运动时间一定小于ACD 对点演练2 (2021湖南卷)带电粒子流的磁聚焦和磁控束是薄膜材料制备的关键技术之一。带电粒子流(每个粒子的质量为m、电荷量为+q)以初速度v垂直进入磁场,不计重力及带电粒子之间的相互作用。对处在xOy平面内的粒子,求解以下问题。(1)如图甲所示,宽度为2r1的带电粒子流沿x轴正方向射入圆心为A(0,r1)、半径为r1的圆形匀强磁场中,若带电粒子流经过磁场后都汇聚到坐标原点O,求该磁场磁感应强度B1的大小。甲 (2)如图甲所示,虚线框为边长等于2r2的正方形,其几何中心位于C(0,-r2)。在虚线框内设计一个区域面积最小的匀强磁场,使汇聚到O点的带电粒子流经过该区域后宽度变为2r2,并沿x轴正方向射出。求该磁场磁感应强度B2的大小和方向,以及该磁场区域的面积(无需写出面积最小的证明过程)。甲 (3)如图乙所示,虚线框Ⅰ和Ⅱ均为边长等于r3的正方形,虚线框Ⅲ和Ⅳ均为边长等于r4的正方形。在Ⅰ、Ⅱ、Ⅲ和Ⅳ中分别设计一个区域面积最小的匀强磁场,使宽度为2r3的带电粒子流沿x轴正方向射入Ⅰ和Ⅱ后汇聚到坐标原点O,再经过Ⅲ和Ⅳ后宽度变为2r4,并沿x轴正方向射出,从而实现带电粒子流的同轴控束。求Ⅰ和Ⅲ中磁场磁感应强度的大小,以及Ⅱ和Ⅳ中匀强磁场区域的面积(无需写出面积最小的证明过程)。乙(2)如图所示 (3)如图所示 突破三　交变电磁场问题解决带电粒子在交变电磁场中的运动问题的基本思路: 【例3】 如图甲所示,水平放置的足够长的平行金属板P和Q间距为d,两板间存在周期性变化的电场或磁场。P、Q间的电势差UPQ随时间的变化规律如图乙所示,磁感应强度B随时间变化的规律如图丙所示,磁场方向垂直纸面向里为正方向。t=0时刻,一质量为m、电荷量为+q的粒子(不计重力),以初速度v0由P板左端靠近板面的位置,沿平行于板面的方向射入两板之间,q、m、d、v0、U0为已知量。甲 乙丙(1)若仅存在交变电场,要使粒子飞到Q板时,速度方向恰好与Q板相切,求交变电场周期T。(2)若仅存在匀强磁场,且满足 ,粒子经一段时间恰能垂直打在Q板上(不考虑粒子反弹),求击中点到出发点的水平距离。(2)仅存在磁场时,带电粒子在匀强磁场中做半径为r的匀速圆周运动,有 要使粒子能垂直打到Q板上,在交变磁场的半个周期内,粒子轨迹的圆心角设为90°+θ,如图所示由几何关系得r+2rsin θ=d解得θ=30°则粒子打到Q板的位置距出发点的水平距离为对点演练3 如图甲所示,在xOy平面内存在大小随时间周期性变化的磁场和电场,变化规律分别如图乙、丙所示(规定垂直纸面向里为磁场的正方向、沿y轴正方向电场强度为正)。在t=0时刻由原点O发射初速度大小为v0、方向沿y轴正方向的带负电粒子。v0、t0、B0为已知量,粒子的比荷为 ,不计粒子的重力。甲 乙丙(1)当t=t0时,求粒子的位置坐标。(2)若t=5t0时粒子回到原点,求0~5t0时间内粒子距x轴的最大距离。(3)若粒子能够回到原点,求满足条件的所有E0值。(2)粒子在t=5t0时回到原点,运动轨迹如图甲所示 甲 (3)如图乙所示,设带电粒子在x轴下方做圆周运动的轨迹半径为r2',由几何关系可知,要使粒子能够回到原点,则必须满足n(2r2'-2r1)=2r1(n=1,2,3,…)乙