河南省开封市2023届九年级上学期期末考试数学试卷(含解析)

这是一份河南省开封市2023届九年级上学期期末考试数学试卷(含解析)，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
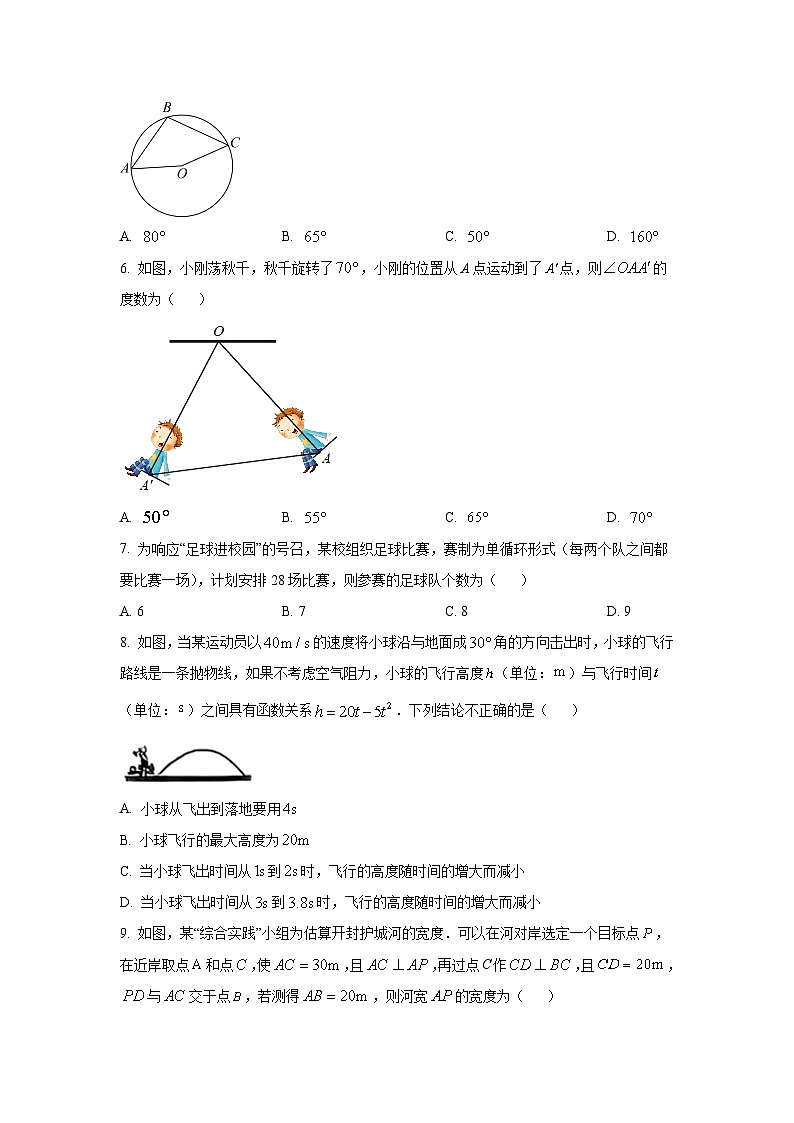
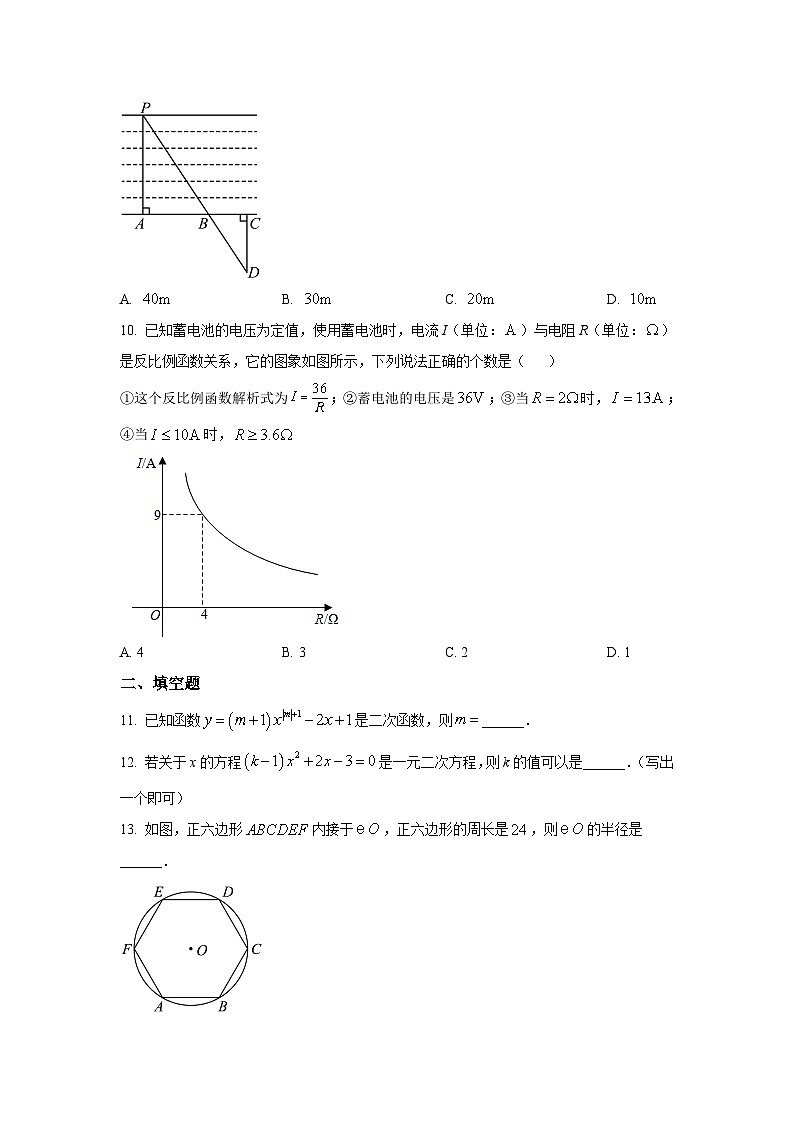
开封市2022—2023学年第一学期期末考试九年级数学试卷一、选择题（下列各题均有四个答案，其中只有一个是正确的）1. 2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（    ）A.  B.  C.  D. 2. 已知点在反比例函数的图象上，则点P关于原点对称的点的坐标是（    ）A.  B.  C.  D. 3. 下列事件中，属于随机事件的是（    ）A. 打开电视机，正在播放广告B. 在装有红球的袋中，摸出黄球C. 正五边形的每个内角都等于108°D. 2022年11月21日—12月18日，在卡塔尔举行了第22届世界杯足球赛4. 若关于x的方程，其中a在数轴上的对应点如图所示，则此方程的根的情况是（    ）A. 无法确定 B. 无实根C. 有两个不相等的实数根 D. 有两个相等的实数根5. 如图，点、、均在上，当时，则的度数是（    ）A.  B.  C.  D. 6. 如图，小刚荡秋千，秋千旋转了，小刚的位置从A点运动到了点，则的度数为（    ）A.  B.  C.  D. 7. 为响应“足球进校园”的号召，某校组织足球比赛，赛制为单循环形式（每两个队之间都要比赛一场），计划安排28场比赛，则参赛的足球队个数为（    ）A. 6 B. 7 C. 8 D. 98. 如图，当某运动员以的速度将小球沿与地面成角的方向击出时，小球的飞行路线是一条抛物线，如果不考虑空气阻力，小球的飞行高度（单位：）与飞行时间（单位：）之间具有函数关系．下列结论不正确的是（    ）A. 小球从飞出到落地要用B. 小球飞行的最大高度为C. 当小球飞出时间从到时，飞行的高度随时间的增大而减小D. 当小球飞出时间从到时，飞行的高度随时间的增大而减小9. 如图，某“综合实践”小组为估算开封护城河的宽度．可以在河对岸选定一个目标点，在近岸取点和点，使，且，再过点C作，且，与交于点，若测得，则河宽的宽度为（    ）A.  B.  C.  D. 10. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：）与电阻R（单位：）是反比例函数关系，它的图象如图所示，下列说法正确的个数是（    ）①这个反比例函数解析式为；②蓄电池的电压是；③当时，；④当时，A. 4 B. 3 C. 2 D. 1二、填空题11. 已知函数是二次函数，则______．12. 若关于x的方程是一元二次方程，则k的值可以是______．（写出一个即可）13. 如图，正六边形内接于，正六边形的周长是，则的半径是______．14. 袁隆平院士被誉为“世界杂交水稻之父”，为研究出高产水稻付出了毕生心血．他的研究团队在某次实验中，针对水稻颗粒的克数是否达标进行了称重评估，结果如下：每批粒数n100300400600100015002000…达标粒数m9628738257796014421920…达标率0.96009570.9550.9620.9600.9610.960…则水稻克数达标的概率估计值是______．15. 如图，为半圆的直径，半径，先将该半圆沿直线剪开得到两个圆心角为的扇形，再把两个扇形经平移，使点与点，点与点分别重合（如图放置），则图中重叠部分（阴影部分）的面积为______．三、解答题16. 解下列方程：（1）（2）17. 如图，在平面直角坐标系中（单位长度为1），的三个顶点坐标分别为，，．（1）画出，使与关于原点O成中心对称；（2）画出，使是绕点顺时针旋转90°时得到的图形，并求出在这个旋转过程中，点C走过的弧长．18. 某市为庆祝二十大的召开，贯彻党的二十大精神，组织中学生举办了爱党知识竞赛．现随机抽取了部分学校的学生的测试成绩进行整理后（说明：测试成绩为x（分），分为5个等级，A等：；B等：；C等：；D等：；E等：），绘制成如下不完整的条形统计图和扇形统计图，请结合统计图回答下列问题：（1）在这次调查中，抽取学生总人数是______，C组对应的扇形圆心角的度数是______；（2）请补全条形统计图；（3）某校现从A等级的4个学生中随机抽取2人去参加市赛，小明和小丽正好在这4个人当中，请用树状图法或列表法求小明和小丽都被抽到的概率是多少？19. 如图，小明设计了一个探究杠杆平衡条件的实验：取一根长为100米的匀质木杆，用细绳绑在木杆的中点O并将其吊起来．在中点O的左侧距离中点O为30处挂一个重10N的物体，在中点O的右侧用一个弹簧秤向下拉，使木杆处于水平状态．改变弹簧秤与中点O的距离L（单位：），观察弹簧秤的示数F（单位：N）的变化情况．得出如下几组实验数据：L/1015202530F/N302015a10（1）观察上表实验数据，写出表中a值______．（2）以L的数值为横坐标，F的数值为纵坐标建立如图平面直角坐标系，在坐标系中描出以上表中的数对为坐标的各点，并用平滑的曲线顺次连接这些点；（3）根据所画的图象，求出F与L的函数关系式．20. 如图，为直径，点是上一点，平分，交于点，、交于点．（1）画出过点的的切线，且交的延长线于点；（2）在（1）的条件下，①求证：；②若，，求的长．21. 某公司准备推出一种水杯，经过市场调查发现，该水杯前期的日销售情况如下：进价每个20元，每天销售量y（个）与销售单价x（元/个）之间满足一次函数关系：（1）求销售单价为多少元时，该水杯每天的销售利润最大；（2）经市场反馈，售价高于25元时，若每个水杯每涨价1元，每天要少卖出10个，商场的营销部在调控价格方面，提出了A，B两种营销方案：方案A：每个水杯涨价不超过5元；方案B：每个水杯的利润至少为16元．哪种方案的最大利润较大，并说明理由．22. 双手正面掷实心球是开封市中招体育考试的选考项目，如图①是一名男生双手正面掷实心球，实心球的行进路线是一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图②所示，掷出时起点高度为2m，当水平距离为5m时，实心球行进至最高点4m处．（1）求抛物线的表达式；（2）根据开封市中招体育考试评分标准（男生10.3m），即投掷过程中，实心球从起点到落地点的水平距离大于等于10.30m，此项考试得分为满分10分．该男生在此项考试中是否得满分，请说明理由．（）23. （1）【初步探究】把矩形纸片如图①折叠，，当点的对应点在的中点时，填空：（或”）．（2）【类比探究】如图②，当点的对应点为上的任意一点时，请判断（）中结论是否成立？如果成立，请写出证明过程；如果不成立，请说明理由．（3）【问题解决】在矩形中，，，点为中点，点为线段上一个动点，连接，将沿折叠得到，连接，，当为直角三角形时，长为______．
答案 1. B解：根据中心对称图形的定义，四个选项中，只有B选项的图形绕着某点旋转180°后能与原来的图形重合，故选B．2. D将代入，则，那么，则点关于原点对称的点的坐标故选：D3. A解：A. 打开电视机，正在播放广告，是随机事件，故该选项符合题意；B. 在装有红球的袋中，摸出黄球，是不可能事件，故该选项不符合题意；C. 正五边形的每个内角都等于，是必然事件，故该选项不符合题意；D. 2022年11月21日—12月18日，在卡塔尔举行了第22届世界杯足球赛，是必然事件，故该选项不符合题意；故选：A．4. C，由数轴可知，∴，∴，即方程有两个不相等的实数根，故选C．5. D解：如图，在优弧上取一点，连接，∵四边形是的内接四边形，∴，∵，∴故答案为：D．6. B∵秋千旋转了，小刚的位置从A点运动到了点，∴，，∴，故选B．7. C解：设参赛的足球队为个，根据题意得，解得：或（舍去）答：参赛的足球队为个，故选：C．8. C解：由题意，，令，即，解得：，∴小球从飞出到落地要用，故A正确，不符合题意；∵，最大值为，故B正确，符合题意；∴对称轴为直线，开口向下，当时，飞行的高度随着时间的增大而增大，故C错误，不符合题意；当时，飞行的高度随时间的增大而减小，故D正确，不符合题意；故选：C．9. A解：∵，，∴，又∵，∴，∴,∵，，∴，解得：，故选：A．10. B解：设，图象过，，，蓄电池的电压是，故①正确、②正确， 当时，（），故③错误； 当时，，由图象知：当时，，故④正确；故选：B．11. 解：∵函数是二次函数，∴解得：，故答案为：．12. （答案不唯一）解：∵关于x的方程是一元二次方程，∴解得：，∴的值可以是0（答案不唯一）．故答案为：0（答案不唯一）．13. 解：如图，连接、，的内接正六边形的周长为，边长为，，且，为等边三角形，，即该圆的半径为．故答案为：．14. 解：∵通过大量重复试验后发现，水稻克数达标的频率稳定于，水稻克数达标的概率估计值是故答案为：．15. 解：连接，作于点．，是等边三角形，，，在直角中，，则，则弧和以及围成的阴影部分的面积是：，则故答案为：．16. （1）解：，∴，∴，解得：；（2）解：，∴，∴，即，解得：17. （1）解：如图所示，即为所求（2）解：如图所示，即为所求；∵绕点顺时针旋转，∴点C走过的弧长为18. （1）2000，108    （人），C组人数为（人），C组对应的扇形圆心角的度数为，故答案为2000，108；（2）由（1）得C组人数为600人，条形统计图如下，（3）设小明和小丽和A等级另外2个学生分别为a、b、c、d，列表得： abcda bacadabab cbdbcacbc dcdadbdcd 故共有12种，其中小明和小丽都被抽到的情况共2种，∴小明和小丽都被抽到的概率是．19. （1）    由表格可知，当L为10，F增加了30；当L为15，F增加了20；当L为20，F增加了15；当L为30，F增加了10；∴L与F的积为300；∴，故答案为；（2）（3）由图可知函数为反比例函数，设函数关系式为，将代入得，∴F与L的函数关系式为．20. （1）解：如图所示，（2）①∴是的切线，，∴，∵是的直径，∴，∴，∵平分，∴，∴，∴；②如图，连接，在中，，，∴，∴，∵，∴，在中，，∴，∴，∵是的直径，∴，又，∴，∴，∴，解得：．21. （1）解：设销售利润为，根据题意得，，当时，该水杯每天的销售利润最大∴当销售单价为元时，该水杯每天销售利润最大（2）方案：设销售利润为，设涨价元，；当售价为元时，销售量为个，∴当时，取得最大值为，由（1）可得，方案：销售单价为:，利润为:（元）∴方案的最大利润较大22. （1）解：依题意，设抛物线解析式为，将点代入得，，解得：，∴解析式为：；（2）解：令，即解得：（舍去），，∴该男生在此项考试中得满分．23. （1）∵四边形是矩形，，∴，∵折叠，∴，∴，∴故答案为：．（2）∵四边形是矩形，，∴，∵折叠，∴，∴，∴（3）解：∵折叠，∴，在中，，①当时，三点共线，∵点为中点，∴，在中，∴∴在中，,即,解得：；②当，如图所示，延长交于点，由（2）可得∴,∴∴，在中，，设，则，∴即 解得：，即，综上所述，当为直角三角形时，的长为或，故答案为：或．